Tarjan求强连通分量

[算法定义]

在有向图中，如果两个顶点至少存在一条路径（可以相互通达），则称两个顶点强连通(strongly connected)。

如果有向图G的每两个顶点都强连通，称G是一个强连通图。

非强连通有向图的极大强连通子图，称为强连通分量(strongly connected components)。

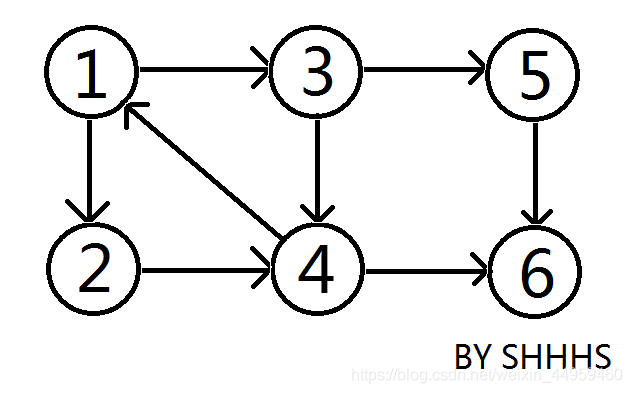
在上图中，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 三个区域可以相互连通，称为这个图的强连通分量。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。

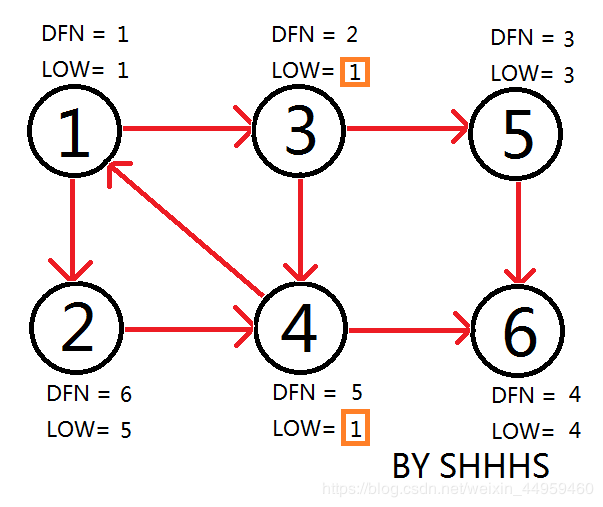
DFN[ i ] : 在DFS中该节点i被搜索的次序(时间戳)。

LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号。

当DFN[ i ]==LOW[ i ]时，已i为根的搜索子树上所有节点是一个强连通分量。

【心得】：如果有环，dfn是传递自己的下一代，low是继承自己的上一代或自己（上一代无环）

搜索时，把当前搜索树中未处理的节点加入一个堆栈。

回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

---

[算法图解]

从1开始dfs搜索，把遍历到的节点加入栈中。

搜索到i=6时，节点都入栈了，此时就进行回溯。

DFN[6]=LOW[6]，以节点6为根的搜索子树是一个强连通分量（节点6没有子树）。

6出栈。

---

依次类推，DFN[5]=LOW[5]，5为强连通分量。

并且5的边也都找完了，5出栈。

接下来回溯到3，4入栈。

---

然后从4找到1，发现节点1已存在。

将1看做根节点往回搜索子节点，子节点LOW[i]=low[根]=1。

子节点low继承的是根的dfn，根的low就是根的dfn，最小的那个

现在只是将1，3，4看做环，1的边还没有找完。

没有找完自然不会进行根节点1成环的回溯出栈操作。

---

继续找1的边，找到2。

再访问4（还在栈中），所以LOW[2]=DFN[4]=5。

那么4的根是2，为什么不继承1的dfn，是为了让缩点与割点代码一致

结果不影响，连通分量还是一起出栈（并染色）

从2返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个强连通分量{1，2，3，4}。

【例】如果2跟1不成环，那么2不会连4，（2将自己抛出）或（2与2的子节点成环整个抛出）

           最后执行到1，再进行1的回溯，组成强连通分量{1，3，4}出栈

---

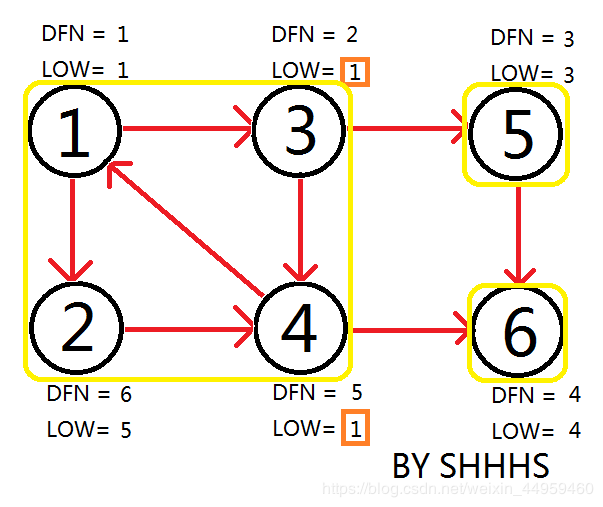
自此算法结束，找到{1，2，3，4}，{5}，{6}三个强连通分量。

---

[代码1]不要慌全解系列

#include
#include
#include
#include 
using namespace std;

struct ss{
	int v;
	int next;
	/*  
	v指节点v 
	next永远指u点->上一个点的边序（1，2，3···）
	边序 即u到其他点（上一个点）是第几条边（num） 
	上一条边没有就是-1 
	*/ 
}s[1000]; 

int head[1000];//边序 
int dfn[1000];
int low[1000];
int vis[1000];//相当于栈 
int color[1000];//染色 
int n,m;
int cnt;
int num;
stackst;

void init()
{
	memset(head,-1,sizeof(head));
	memset(vis,0,sizeof(vis));
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	//memset(color,0,sizeof(color));	
	num=0;
	cnt=0;
}
void add(int u,int v)
{
	s[num].v = v;
	s[num].next = head[u];
	head[u] = num++;
	/*
	将v存进去
	将u->上一个点的边序挂上next
	num一直在++(总边数不会错)
	head[u]更新当前u的边序 			

	如果双向再存u挂v边序 
	eg[num].v = u;
	eg[num].next = head[v];
	head[v] = num++;
	*/ 	
}
void Tarjan(int u)
{
	st.push(u);
	dfn[u] = low[u] = ++cnt;//搜索次序号 
	vis[u]=1;//节点x在栈中
	for(int i = head[u]; i != -1; i = s[i].next)
	{
		//通过对u点上一个边序的挂钩
		//构造对连接u点的所有边数遍历查找对应v点 
		int v = s[i].v;
		if(!dfn[v])//不曾访问过 
		{
			Tarjan(v);//找v点 
			low[u] = min(low[u],low[v]);
			/* 
			根节点的dfn值是区分不同环的值
                        low是为了让这个环都等dfn[根]
                        low[根]可能不等dfn[根]
                        根的low继承根的根的dfn 
			1.如果v是根节点
			  不论只有v一个点还是有一个环 
			  low[v]确实永远比low[u]大(u比v先入)
			  v的环low值=dfn[v]都比low[u]的大 
			  v不对u产生影响
			2. 
			  如果v点与u点成环
			  那么顺着v点或v连着的点找下去
			  总有一个能连到根节点
			  low值回溯的时候继承根的dfn值
                          根的dfn是这个环里面最小的
			  low[v]等于dfn[根]
			  v对u产生影响->low[u]=low[v] 
			*/ 
		}
		else if(vis[v])//访问过但还在栈中 
			/*
			因为根u点还没有将边都找完
			出栈的点都是根节点边已经找完的点或者环 
			已经没有与剩下的点有任何关系才能出 
			*/ 
			low[u] = min(low[u],dfn[v]);
			/*
			这相当于根节点有两个分叉口a,b 
			并且a找到已经在栈中的b
				  
			那么这一步其实也可以写成 
			low[u] = min(low[u],low[v]);
                        反正连到一个环了
		
                        目的是为了让缩点与割点的代码一致 
                        区分相连的环的根有不同的dfn
                        无向图找割点用的

                        但是缩点是将一起出栈的点缩成一个点（染成一个色）
	                对于缩点结果都无影响	
			*/
	}	

	if(dfn[u]==low[u])//找一遍再是强连通分量 
	{
		int now;
		do{	//取出包括u的环 
			now=st.top();
			color[now]=u; //染色 
			vis[now]=0;
			st.pop();
		}while(now!=u);
	}
	return;	
} 
void out()
{
	for(int i=1;i<=n;i++)
		printf("%d ",i);
	printf("\n");
	for(int i=1;i<=n;i++)
		printf("%d ",color[i]);
	printf("\n");
}

int main()
{
	while(~scanf("%d%d",&n,&m) && (m+n))
	{
		init();
		int u,v;
		while(m--)
		{
			scanf("%d%d",&u,&v);	
			add(u,v);
		}	
		//为了防止一个图里有不相连的两个或多个树 
		for(int i=1;i<=n;i++) 
			if(!dfn[i]) 
				Tarjan(i);
		out();
	} 
	return 0; 
} 

---

[代码2]

若只是缩点，求强连通分量染色，不与割点代码一致，就不需要用栈

#include
#include
#include
#include 
#include
using namespace std;

int dfn[1000];
int low[1000];//就相当于颜色，一个环一个low=dfn[根] 
int vis[1000];
int n,m;
int cnt;
stackst;
vectorvc[1000]; 

void init()
{
	memset(vis,0,sizeof(vis));
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));	
	cnt=0;
}

void Tarjan(int u)
{
	st.push(u);
	dfn[u] = low[u] = ++cnt;
	vis[u]=1;
	for(int i = 0; i < vc[u].size(); i++)
	{
		int v = vc[u][i];
		if(!dfn[v])
		{
			Tarjan(v);
			low[u] = min(low[u],low[v]);
		}
		else 
			low[u] = min(low[u],low[v]);	
	} 
	return;	
} 
void out()
{
	for(int i=1;i<=n;i++)
		printf("%d ",i);
	printf("\n");
	for(int i=1;i<=n;i++)
		printf("%d ",low[i]);
	printf("\n");
}

int main()
{
	while(~scanf("%d%d",&n,&m) && (m+n))
	{
		init();
		int u,v;
		while(m--)
		{
			scanf("%d%d",&u,&v);	
			vc[u].push_back(v);
		}	
		for(int i=1;i<=n;i++) 
			if(!dfn[i]) 
				Tarjan(i);
		out();
	} 
	return 0; 
} 

---