直击信息本质 - 信息论

前言

在信息论中，认为信源输出的消息是随机的。即在未收到消息之前，是不能肯定信源到底发送什么样的消息。信源随机总数即为信息总量。信息论，熵的计算从理论上告诉了算法或逻辑的最好性能上限。

定义

信息熵

1. 信息熵的计算公式为
   
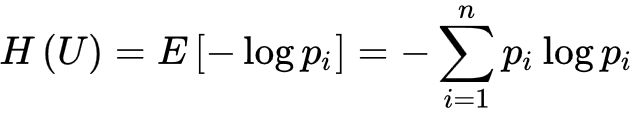
   式中对数一般取2为底，单位为比特。但是，也可以取其它对数底，采用其它相应的单位，它们间可用换底公式换算。(信息量的计算公式)

2. 以上的定义可以简单理解，假设有一个数字值为0-1023之间，总共有1024种情况，那么它的信息量为log2(1024) = 10 bit。如果一个数字的值为0-1之间，那么信息量为log2(2) = 1 bit。

3. 用通俗点话来说信息量就是表达一个数字最少需要多少位的二进制才能表达。0 - 1023之间的数字需要10位二进制才能表达，所以信息量为10bit。

4. 公式可以简单理解为，一个信息有多少种可能的情况N，那么信息量为log2(N) bit 。

经典一问

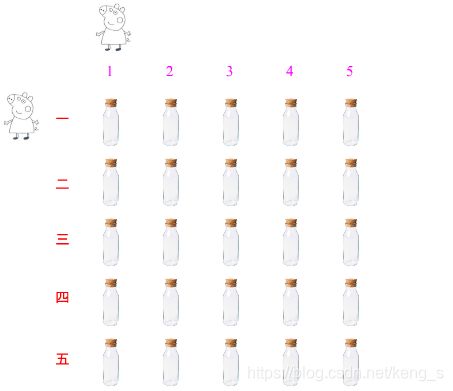
25桶水，其中一桶有毒，猪喝毒水后会在15分钟内死去，想用一个小时找到这桶毒水，至少需要几头猪？

限制条件：
(1)一滴毒水足以导致一头猪的死亡。
(2)死亡时间为15分钟内不确定的某个时间点。
(3)其死亡只是毒水导致的，不会有其他因素导致死亡。
(4)猪的承水量无穷大，且假设饮一桶花费时间为零。
(5)每桶水的量无穷大。

信息分析与结果

(1)25桶水，其中有1桶毒水，那么毒水可能出现在1-25之间的任意一桶，如果需要确定是那一桶那么需要的信息量为log2(25) ≈ 4.64 bit 。

(2)猪喝毒水后会在15分钟内死去，想用一个小时找到这桶毒水。如果充分利用信息，猪的死亡时间为15，30，45，60分这几个节点死亡与不死，共计五中情况。那么一头猪能提供的信息为log2(5) ≈ 2.32 bit。

(3)从信息的角度计算，一头猪能提供的信息为2.32 bit而需要4.64 bit信息才能确定毒水位置，那么4.64/2.32 = 2 ,最少需要2头猪。

算法设计

(1)把水瓶分为五行5列。

(2)在0，15，30，45这四个时间节点，分别让猪A喝完1，2，3，4行，猪B喝完1，2，3，4列的水。

(3)如果猪在15，30，45，60分内死亡，那么代表行或列为1，2，3，4。如果猪没有死亡，则代表5。

(4)假设猪A 在15内死亡，那么毒水一定在第一行。猪B没有死亡，那么毒水一定在第5列，则毒水是 第5瓶。(第一排第5列)

图

算法原理

(1)每头猪喝的水分为5个集合(因为一小时内最多喝4次，所以最多能提供五种信息状态)，每头猪在同一个时间段喝下的水，它们之间有5分之1的交集。

(2)处于交集的水就是有毒的水，而每个猪喝的水之间的交集为1瓶水，则可以直接定位到毒水。

(3)整个算法的原理都围绕在两个元素集合的交集，让每头猪，每次喝的水之间交集变小。每头猪会从所有的水中获取一次信息。(每头猪会喝遍所有的水，除最后一批，如果喝前四批没问题，那么肯定是最后一批有问题。)

算法拓展

(1)参考上图。

(2)每头猪固定喝一个维度的水，在一个小时内，要喝完总量的5分之4的水，这些水不重复出现。 在0-25这个数量时，可以把数据划分为二维正方形，每次喝其中的一条线(线与X,Y轴平行)。在26-125这个数量时，可以把数据划分为三维正方体，每次喝其中一个面(面与X,Y,Z平面平行)。以此类推。

(3)采用5进制编码，通过总数25可以得这log5(25) = 2，可以得知要表达十进制的25，使用5进制需要2位。当总数是125时log5(125) =3 ，可以知道要表达十进制的125，使用5进制需要3位。位数就是需要的猪的头数，即此问题中头数与水数量N的关系为log5(N)。(算出来的数值需要向上取整)

(4)假设喝水在10进制下为125瓶，则5进制下有log5(125) =3 位，有猪A,B,C。在0分钟的时候A喝下XX1，B喝下X1X，C喝下1XX的水。在15分钟的时候A喝下XX2，B喝下X2X，C喝下2XX的水。以此类推。(其中XX1代表只要是末位是1的水，例001,421,301等)最后根据A,B,C猪死亡的时间即可确定毒水。

问题变种

变种1

假设是1000桶水的时候，需要多少头猪？

(1) 使用上面算法的结论公式为，log5(N) = log5(1000) ≈ 4.29 = 5 头。

(2)使用信息论计算公式为，log2(1000) ≈ 9.96 bit,一头猪能提供的信息为log2(5) ≈ 2.32 bit, 9.96/ 2.32 ≈4.3 = 5 头。

变种2

假设是1000桶水的时候，总时间只有15分钟，需要多少头猪？

(1) 使用上面算法的结论公式为，log2(n) = log2(1000) ≈ 9.96 = 10 头。（总时间只有15分钟，那么只够喝一次水，所以只能得到两个信息状态。）

(2)使用信息论计算公式为，log2(1000) ≈ 9.96 bit,一头猪能提供的信息为log2(2) = 1 bit, 9.96/ 1 = 10 头。

关联

排序

(1) N个元素排序，那么可能的情况为全排列，也就是说，总共有N!(N的阶乘)种情况。

(2) N个元素排序,需要的信息总量最少为log2(N!) = log2(123…*n) = log2(1)+log2(2)+log2(3)…+log2(n) ≈ N log2(N)， 则信息总量最少需要N log2(N)

(3)快速排序，最佳情况为N log2(N) 次循环判断，每一次判断可以产生一个布尔值，也就是1 bit的信息，那么信息总量为 1 * N log2(N) bit 。

(4)桶排序，最佳情况，桶数量M = N， 元素在哪个桶中可以提供的信息量为log2(N)。那么，N个元素的信息总量为N * log2(N) bit。

(5)上面计算可以得知，快速排序或桶排序获取的信息量是大于所需总信息量。

存送门

排序