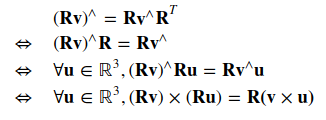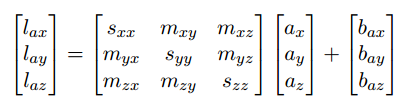IMU测量模型、运动模型、误差模型
目录
- IMU测量模型
- IMU运动模型
- 旋转量求导
- 科氏加速度
- IMU 误差模型
- 确定性误差
- 确定性误差误差标定
- 六面法标定加速度
- 六面法标定陀螺仪
- 温度相关的参数标定
- 随机误差
- 高斯白噪声与随机游走
- 高斯白噪声
- Bias 随机游走
- 随机误差的标定
- 艾伦方差标定
- IMU 数学模型
IMU测量模型
-
MEMS 加速度计工作原理
测量原理可以用一个简单的质量块 + 弹簧 + 指示计来表示
加速度计测量值 a m a_m am为弹簧拉力对应的加速度
a m = f m = a − g a_m=\frac{f}{m}=a-g am=mf=a−g
其中m为质量块质量，a为物体在世界（惯性）坐标系下的实际加速度。 -
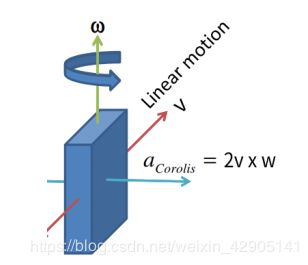
陀螺仪测量原理
陀螺仪的测量值即为IMU在body坐标系下的旋转角速度，要通过运动学模型转换到惯性坐标系下 ，按测量原理分有振动陀螺，光纤陀螺等。低端 MEMS 陀螺上一般采用振动陀螺原理，通过测量 Coriolisforce 来间接得到角速度。
在旋转坐标系中，运动的物体受到科氏力作用
MEMS 陀螺仪：一个主动运动轴 + 一个敏感轴
IMU运动模型
旋转量求导
首先，如下图所示，考虑一个从原点出发的向量 r 绕单位轴 u 旋转，角速度大小为 θ˙。
角速度矢量可以表示为 ω = θ ˙ u {\boldsymbol \omega}=\dot{\theta}\bf u ω=θ˙u，易得向量 r 末端点 P 的速度矢量，即 r的时间一阶导为
d r d t = ω × r \frac{d{\bf r}}{dt} = {\boldsymbol \omega} \times {\bf r} dtdr=ω×r
坐标系 {B} 绕单位轴 u 旋转，如上所述，其三个轴的时间一阶导同样为
d i B d t = ω × i B , d j B d t = ω × j B , d k B d t = ω × k B \frac{d{\bf i}_B}{dt} = {\boldsymbol \omega} \times {\bf i}_B, \frac{d{\bf j}_B}{dt} = {\boldsymbol \omega} \times {\bf j}_B, \frac{d{\bf k}_B}{dt} = {\boldsymbol \omega} \times {\bf k}_B dtdiB=ω×iB,dtdjB=ω×jB,dtdkB=ω×kB
[ i B j B k B ] [ {\bf i}_B \quad {\bf j}_B \quad {\bf k}_B ] [iBjBkB] 实际上就是坐标系 {B} 相对于参考坐标系的旋转矩阵 R，R的时间一阶导为
R ˙ = [ ω × i B ω × j B ω × k B ] = ω × R \dot{\bf R} = [ {\boldsymbol \omega} \times {\bf i}_B \quad {\boldsymbol \omega} \times {\bf j}_B \quad {\boldsymbol \omega} \times {\bf k}_B ] = {\boldsymbol \omega} \times {\bf R} R˙=[ω×iBω×jBω×kB]=ω×R
叉乘运算可以转化为负对称矩阵的乘法：
R ˙ = ω ∧ R \dot{\bf R} = {\boldsymbol \omega}^{\land} {\bf R} R˙=ω∧R
其中负对称矩阵 ω ∧ {\boldsymbol \omega}^{\land} ω∧为
ω ∧ = [ 0 − ω 3 ω 2 ω 3 0 − ω 1 − ω 2 ω 1 0 ] % ω∧=⎣⎡0ω3−ω2−ω30ω1ω2−ω10⎦⎤
这里的角速度 ω 是在参考坐标系下表达的，角速度也经常表达在体坐标系 {B} 下，记为 B ω = R T ω {}^B{\boldsymbol \omega} = {\bf R}^T{\boldsymbol \omega} Bω=RTω，即 ω = R B ω {\boldsymbol \omega} = {\bf R}{}^B{\boldsymbol \omega} ω=RBω
上式也可以写作：
R ˙ = w ∧ R = ( R B w ) ∧ R = R ∧ w R T R = R ( B w ) ∧ \dot{\bf R} =w^{\land}R=(R^Bw)^{\land}R=R{}^{\land}wR^TR= R({}^Bw)^{\land} R˙=w∧R=(RBw)∧R=R∧wRTR=R(Bw)∧
证：对任意旋转矩阵 R 和三维向量 v，都有 ( R v ) ∧ = R v ∧ R T ({\bf R v})^{\land} = {\bf Rv^{\land}R}^T (Rv)∧=Rv∧RT
最后一式利用向量叉乘的旋转变换不变性可证，即，对于任意 v , u ∈ R 3 {\bf v,u}\in \mathbb{R}^3 v,u∈R3永远有
( R v ) × ( R u ) = R ( v × u ) ({\bf Rv})\times({\bf Ru})={\bf R(v\times u)} (Rv)×(Ru)=R(v×u)
从三维几何的角度来理解：v,u 是任意两个三维向量，(v×u) 是一个和 v,u 都垂直、大小为 |v||u|sin(u,v) 的三维向量；将 v,u,v×u 三个向量都经过同一个旋转，它们的相对位姿和模长都不会改变，所以 (Rv) 和 (Ru) 的叉乘仍是 R(v×u)。
科氏加速度
这次把绕惯性系 {A} 中固定单位轴 u 旋转的 {B} 作为参考坐标系。考虑下图， 点 P 相对于 {B} 运动，记 B r {}^Br Br 分别为 P 在 {B} 下的坐标，r 为 P 的绝对坐标（即 {A} 下坐标）， R 仍为 {B} 相对于 {A} 的旋转矩阵，易知 r = R B r r=R{}^Br r=RBr。
r = R B r r=R{}^Br r=RBr求一阶时间导
v = r ˙ = R ˙ B r + R B r ˙ = ω ∧ R B r + R B r ˙ {\bf v} = \dot{\bf r} = \dot{\bf R} {}^B{\bf r} + {\bf R}^B\dot{\bf r} = {\boldsymbol \omega}^{\land}{\bf R}{}^B{\bf r}+ {\bf R}^B\dot{\bf r} v=r˙=R˙Br+RBr˙=ω∧RBr+RBr˙
记P在 {B}下速度为 B v {}^Bv Bv，于是
v = w ∧ r + R B = w × r + v r v = w^{\land}r+ {R}^B{}= w \times r+ v_r v=w∧r+RB=w×r+vr
v r {\bf v}_r vr来表达「相对速度」的概念，准确定义为 P 相对于 {B} 的速度，在惯性系 {A} 下的表达
再对求时间导：
在旋转坐标系下观察，运动的物体（运动方向和旋转轴不为同一个轴时）会受到科氏力的作用。
- 第一项中 α {\boldsymbol \alpha} α为 {B} 的角加速度，所以第一项的物理意义是 {B} 旋转所造成的 P 的切向加速度
- 第二项是 {B} 旋转所造成的向心加速度
- 第三项比较特殊，为 {B} 的旋转运动与 P 相对 {B} 的平移运动耦合产生的加速度，称为科氏加速度
- 第四项为 P 相对于 {B} 的加速度，但在惯性系{A}下表达，类似于 v r {\bf v}_r vr
IMU 误差模型
加速度计和陀螺仪的误差可以分为：确定性误差，随机误差。
- 确定性误差可以事先标定确定，包括： bias, scale …
- 随机误差通常假设噪声服从高斯分布，包括：高斯白噪声， bias
随机游走…
确定性误差
- Bias ，Scale
理论上，当没有外部作用时， IMU 传感器的输出应该为 0，但实际数据存在一个偏置 b。
- 加速度计 bias 对位姿估计的影响：
v e r r = b a t ， p e r r = 1 2 b a t 2 v_err=b_at，p_err=\frac{1}{2}b_at^2 verr=bat，perr=21bat2 - scale 可以看成是实际数值和传感器输出值之间的比值
- Nonorthogonality/Misalignment Errors(非正交/错位错误）
- 其他确定性误差
- Run-to-Run Bias/Scale Facto
- In Run (Stability) Bias/Scale Factor
- Temperature-Dependent Bias/Scale Factor
确定性误差误差标定
六面法标定加速度
bias 和 scale factor
六面法是指将加速度计的 3 个轴分别朝上或者朝下水平放置一段时间，采集 6 个面的数据完成标定。如果各个轴都是正交的，那很容易得到 bias 和 scale：
其中, l l l为加速度计某个轴的测量值， g为当地的重力加速度
（Nonorthogonality/Misalignment Errors)
多轴 IMU 传感器制作的时候，由于制作工艺的问题，会使得 xyz 轴可能不垂直，如下图所示。
考虑轴间误差的时候，实际加速度和测量值之间的关系为：
水平静止放置 6 面的时候，加速度的理论值为
对应的测量值矩阵 L ：
利用最小二乘就能够把12个变量求出来。
六面法标定陀螺仪
- 六面法标定陀螺仪 bias 和 scale factor
和加速度计六面法不同的是，陀螺仪的真实值由高精度转台提供，这
里的 6 面是指各个轴顺时针和逆时针旋转。
参考：https://blog.csdn.net/CSDN_XCS/article/details/90339761
温度相关的参数标定
- 目的：这个标定的主要目的是对传感器估计的 bias 和 scale 进行温度补偿，获取不同温度时 bias 和 scale 的值，绘制成曲线。
- 两种标定方法：
• soak method: 控制恒温室的温度值，然后读取传感器数值进行标定。
• ramp method：记录一段时间内线性升温和降温时传感器的数据来进行标定。
随机误差
高斯白噪声与随机游走
高斯白噪声
高斯白噪声的高斯指的是概率分布为正态分布，白噪声指的是其二阶矩不相关，一阶矩为常数。故把瞬时值的概率分布服从高斯分布，功率谱密度服从均匀分布的噪声称为高斯白噪声
IMU 数据连续时间上受到一个均值为 0，方差为 σ 2 σ^2 σ2，各时刻之间相互独立的高斯过程 n(t)：
E [ n ( t ) ] = 0 E[n(t)]=0 E[n(t)]=0
E [ n ( t 1 ) n ( t 2 ) ] = σ 2 δ ( t 1 − t 2 ) E[n(t_1)n(t_2)]=σ^2δ(t_1−t_2) E[n(t1)n(t2)]=σ2δ(t1−t2)
自相关函数的数学定义： R ( τ ) = ∫ ∞ − ∞ x ( t ) x ( t − τ ) d t R(τ)=∫^{−∞}_∞ x(t)x(t−τ)dt R(τ)=∫∞−∞ x(t)x(t−τ)dt
其中 δ ( ) δ() δ() 表示狄拉克函数
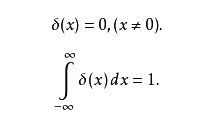
白噪声的离散化
实际上， IMU 传感器获取的数据为离散采样，离散和连续高斯白噪声的方差之间存在如下转换关系：
n d [ k ] ≜ n ( t 0 + Δ t ) ≃ 1 Δ t ∫ t 0 t 0 + Δ t n ( τ ) d t n_d[k] \triangleq n(t_0+\Delta t)\simeq\frac{1}{\Delta t}\int_{t_0}^{t_0+\Delta t}n(\tau)dt nd[k]≜n(t0+Δt)≃Δt1∫t0t0+Δtn(τ)dt
E ( n d [ k ] 2 ) = E ( 1 Δ t 2 ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t n ( τ ) n ( t ) d τ d t ) = E ( σ 2 Δ t 2 ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t δ ( t − τ ) d τ d t ) = E ( σ 2 Δ t ) \begin{aligned} E(n_d[k]^2) & = E(\frac{1}{\Delta t^2}\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}n(\tau)n(t)d \tau dt) \\ &= E( \frac{\sigma^2}{\Delta t^2}\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}\delta(t-\tau)d \tau dt)\\ &= E(\frac{\sigma^2}{\Delta t}) \end{aligned} E(nd[k]2)=E(Δt21∫t0t0+Δt∫t0t0+Δtn(τ)n(t)dτdt)=E(Δt2σ2∫t0t0+Δt∫t0t0+Δtδ(t−τ)dτdt)=E(Δtσ2)
即:
n d [ k ] = σ d w [ k ] nd[k] = σ_dw[k] nd[k]=σdw[k]
其中： w [ k ] ∼ N ( 0 , 1 ) w[k] ∼ N(0, 1) w[k]∼N(0,1)， σ d = σ 1 △ t \sigma_d=\sigma \frac{1}{\sqrt{\bigtriangleup t}} σd=σ△t1
也就是说高斯白噪声的连续时间到离散时间之间差一个 1 △ t \frac{1}{\sqrt{\bigtriangleup t}} △t1 ，√∆t 是传感器的采样时间。
Bias 随机游走
通常用维纳过程 (wiener process) 来建模 bias 随时间连续变化的过程，离散时间下称之为随机游走
b ˙ ( t ) = n ( t ) = σ b w ( t ) \dot{b}_{(t)}=n(t)=\sigma_bw(t) b˙(t)=n(t)=σbw(t)\sigma_b
其中 w 是方差为 1 的白噪声
离散和连续之间的转换：
b d [ k ] ≜ b ( t 0 ) + ∫ t 0 t 0 + Δ t n ( t ) d t b_d[k] \triangleq b(t_0) + \int_{t_0}^{t_0+\Delta t}n(t)dt bd[k]≜b(t0)+∫t0t0+Δtn(t)dt E ( ( b d [ k ] − b d [ k − 1 ] ) 2 ) = E ( ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t n ( t ) n ( τ ) d τ d t ) = E ( σ b 2 ∫ t 0 t 0 + Δ t ∫ t 0 t 0 + Δ t δ ( t − τ ) d τ d t ) = E ( σ b 2 Δ t ) \begin{aligned} E((b_d[k]-b_d[k-1])^2) &=E(\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}n(t)n(\tau)d \tau dt)\\ &= E({\sigma_{b}^2}\int_{t_0}^{t_0+\Delta t}\int_{t_0}^{t_0+\Delta t}\delta(t-\tau)d \tau dt)\\ &= E(\sigma_{b}^2\Delta t) \end{aligned} E((bd[k]−bd[k−1])2)=E(∫t0t0+Δt∫t0t0+Δtn(t)n(τ)dτdt)=E(σb2∫t0t0+Δt∫t0t0+Δtδ(t−τ)dτdt)=E(σb2Δt)
即：
b d [ k ] = b d [ k − 1 ] + σ b d w [ k ] b_d[k] = b_d[k − 1] + σ_{bd}w[k] bd[k]=bd[k−1]+σbdw[k]
其中：
w [ k ] ∼ N ( 0 , 1 ) , σ b d = σ b △ t w[k] ∼ N(0, 1),σ_{bd} = σ_b\sqrt{\bigtriangleup t} w[k]∼N(0,1),σbd=σb△t
bias 随机游走的噪声方差从连续时间到离散之间需要乘以 △ t \sqrt{\bigtriangleup t} △t
随机误差的标定
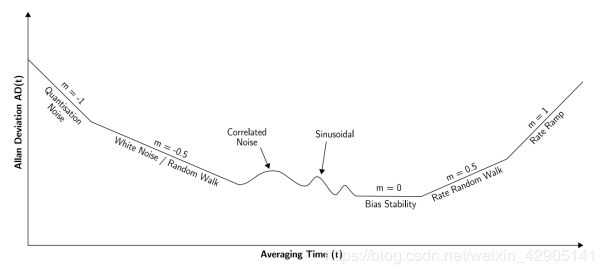
艾伦方差标定
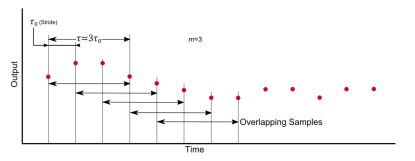
Allan 方差法是 20 世纪 60 年代由美国国家标准局的 David Allan 提出的，它是一种基于时域的分析方法。
具体的流程如下：
- 保持传感器绝对静止获取数据
- 对数据进行分段，设定时间段的时长，如下图所示
- 将传感器数据按照时间段进行平均
- 计算方差，绘制艾伦曲线，得到的艾伦曲线如下图所示:
Allan方差法可用于5种随机误差的标定：
参考：VIO标定IMU随机误差：Allan方差法
陀螺 Allan 方差分析
IMU 数学模型
以 ECI 为参考坐标系（由于 ECI 为惯性系，不需要考虑地球自转）：
忽略 scale 的影响，只考虑白噪声和 bias 随机游走：
IMU的真实值： w b , a b w^b,a^b wb,ab
IMU的测量值： w ~ , a ~ b \widetilde{w},\widetilde{a}^b w ,a b
IMU机体系即b系，w系表示世界坐标系。
w ~ = w b + b g + n g a ~ b = a b + b a + n a = q b w ( a w + g w ) + b a + n a \begin{aligned} \widetilde{w}&=w^b +b^g+n^g\\ \widetilde{a}^b&=a^b+b^a+n^a\\&=q_{bw}(a^w+g^w)+b^a+n^a \end{aligned} w a b=wb+bg+ng=ab+ba+na=qbw(aw+gw)+ba+na
考虑高斯白噪声项，有：
w b = w ~ − b g − n g a w = q w b ( a ~ b − b a − n a ) − g w \begin{aligned} &w^b=\widetilde{w} -b^g-n^g\\ &a^w=q_{wb}(\widetilde{a}^b-b^a-n^a)-g^w \end{aligned} wb=w −bg−ngaw=qwb(a b−ba−na)−gw
不考虑高斯白噪声项，有：
w b = w ~ − b g a w = q w b ( a ~ b − b a ) − g w \begin{aligned} &w^b=\widetilde{w} -b^g\\ &a^w=q_{wb}(\widetilde{a}^b-b^a)-g^w \end{aligned} wb=w −bgaw=qwb(a b−ba)−gw
参考：从零开始的 IMU 状态模型推导