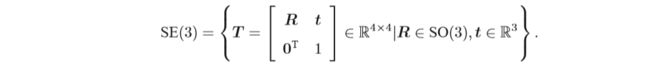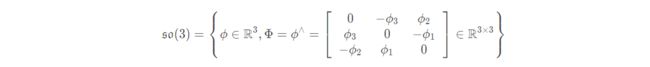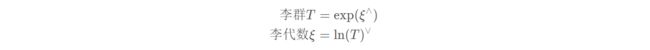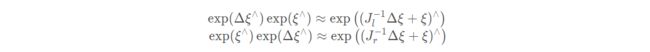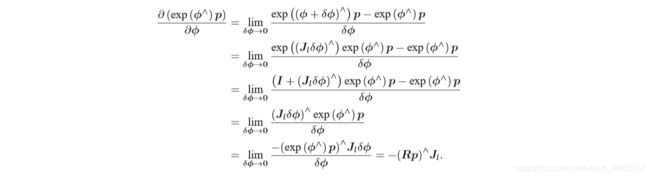视觉SLAM —— 李群与李代数
一、群
1.1 群的定义
群（Group）是一种集合加上一种运算的代数结构。把集合记作A，运算记作 · ，那么群可以记作G = （A，· ），群要求这个运算满足如下条件（封结幺逆——凤姐咬你）：
- 封闭性：∀a1,a2 ∈ A, a1 ·a2 ∈ A.
- 结合律： ∀a1,a2,a3 ∈ A, (a1 ·a2)·a3 = a1 ·(a2 ·a3).
- 幺元：∃a0 ∈ A, s.t. ∀a ∈ A, a0 ·a = a·a0 = a.
- 逆：∀a ∈ A, ∃a−1 ∈ A, s.t. a·a−1 = a0.
.
1.2 李群 SO(3)
李群是指具有连续（光滑）性质的群。
旋转矩阵构成特殊正交群：
1.3 李群 SE(3)
变换矩阵构成特殊欧式群：
二、李代数定义
为什么要引入李代数呢？
因为我们在优化旋转矩阵或变换矩阵的时候，我们要对它们求导，然而根据李群的定义，他们对加法是不封闭的（根据求导的定义，需要加一个小量），只对乘法封闭。因此我们考虑能否引入一个东西，来找到其与李群的关系，而且对加法还封闭，这样我们就能用这个来求导，然后映射回李群上。
.
2.1 李代数定义
每个李群都有与之对应的李代数，描述了李群的局部性质。然而它俩并不是一一对应的关系（最后解释）。
李代数描述了李群的局部性质，准确地说，是单位元附近的 正切空间。
李代数由一个集合 V，一个数域 F 和一个二元运算 [,] 组成，通用的李代数的定义如下：
- 封闭性： ∀X,Y ∈V,[X,Y ] ∈V.
- 双线性 ∀X,Y ,Z ∈V,a,b ∈F, 有：
[aX + bY ,Z] = a[X,Z] + b[Y ,Z], [Z,aX + bY ] = a[Z,X] + b[Z,Y ]. - 自反性： ∀X ∈V,[X,X] = 0.
- 雅可比等价： ∀X,Y ,Z ∈V,[X,[Y ,Z]] + [Z,[X,Y ]] + [Y ,[Z,X]] = 0.
其中二元运算叫 李括号 。
.
2.2 李代数 so(3)
-
李群 SO(3) 对应的李代数 so(3) 是定义在 R3 上的向量，记作 ϕ 。
-
李代数 * se(3)* 的李括号为：
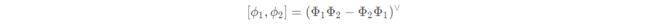
其中∨是∧的的逆运算，表示将反对称矩阵还原为向量。 -
so(3) 和 SO(3) 间的映射关系为：
2.3 李代数 se(3)
-
类似的，李群SE(3) 的李代数 se(3) 是定义在 R6 上的向量。记作 ξ ：
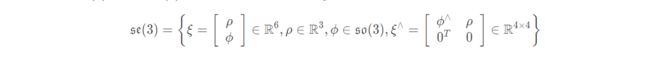
se(3)中每个元素 ξ ，是一个六维向量，前三维ρ表示平移，后三维 ϕ 表示旋转，本质上是 so(3) 的元素。 -
在这里同样使用 ∧ 符号将六维向量扩展成为四维矩阵,但不再表示反对称
-
李代数 se(3) 的李括号和 so(3) 类似:
-
se(3)和SE(3)SE(3)SE(3)间映射关系为
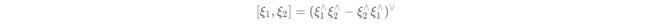
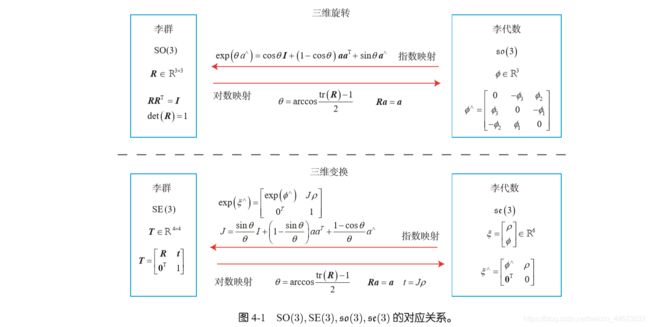
三、李群与李代数转换关系：指数映射和对数映射
3.1 SO(3) 与 so(3) 间的指数与对数映射
3.1.1指数映射
考虑任意旋转矩阵 R，我们知道它满足：
现在，我们说，R 是某个相机的旋转，它会随时间连续地变化，即为时间的函数：R(t)。由于它仍 是旋转矩阵，有
两边对时间求导：
可以看出 R‘(t)R(t)T 是一个反对称矩阵。令（李代数）ϕ^(t) = R’(t)R(t)T 。
两边同时右乘R(t)，且R(t)为正交阵：
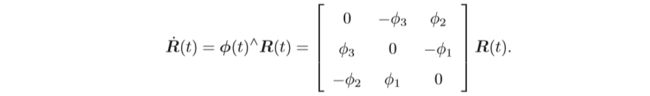
在 t0 附近，设 ϕ 保持为常数 ϕ(t0) = ϕ0，可得：
然后求解常系数微分方程，得：
此时，我们得到了李群SO(3) 和 李代数 SE(3) 的关系，但是ϕ0是一个矩阵，我们没定义过矩阵的指数函数，不清楚怎么求解，那怎么办呢？
用泰勒级数展开求解：
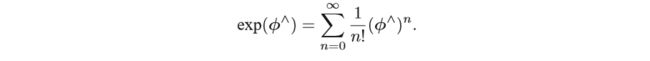
但这个也无法计算，因为我们不可能去计算矩阵的无穷次幂。因此推导了一种计算指数映射的简便方法。
由于ϕ是三维向量，我们可以定义它的模长和它的方向，分别记作θ 和a，于是有ϕ = θa。 这里 a 是一个长度为 1 的方向向量，即∥a∥ = 1。首先，对于 a∧，有以下两条性质：
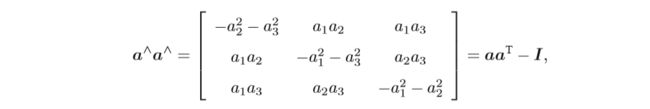
这两个式子提供了处理 a∧ 高阶项的方法。我们可以把指数映射写成：
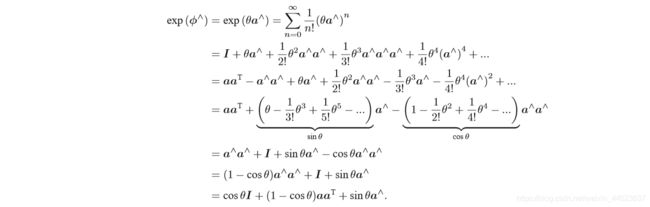
则：
将三维向量 ϕ 分解为其模长θ\thetaθ和方向向量 α ,即ϕ=θα .则从 so(3) 到 SO(3) 的指数映射可表示为:
看最后这个式子是不是有点熟悉呢？
它是不是和罗德里格斯公式如出一辙呢？这表明，so(3) 实际上就是由所 谓的旋转向量组成的空间，而指数映射即罗德里格斯公式。
.
3.1.2 对数映射
反之，如果定义对数映射，也能把SO(3) 中的元素对应 到 so(3) 中：
既然我们知道了李代数是旋转向量，那我们可否根据刚体变换那里直接求得α和 θ 呢？ 可以的，利用迹的性质：
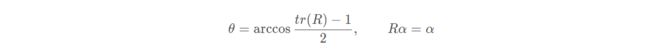
3.2 SE(3) 与 se(3) 间的指数与对数映射
-
从 se(3) 到 SE(3) 的指数映射可表示为:
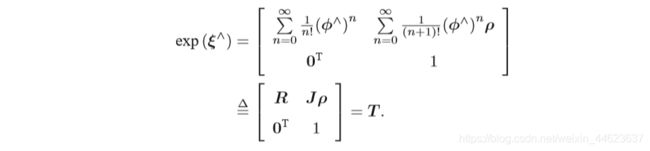
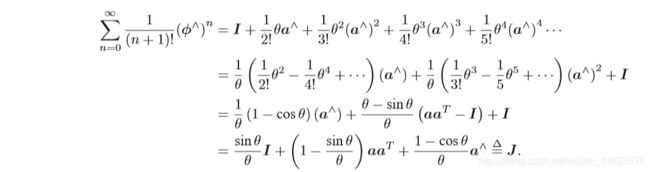
则可以看到平移部分经过指数映射后，发生了一次以J为系数矩阵的线性变换。 -
从SE(3) 到 se(3) 的对数映射为：
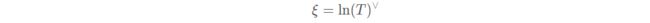
他也有另一种做法：从左上角的R计算旋转向量，二右上角 t 满足：
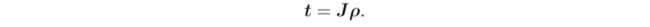
由于 J 可以由 ϕ 得到，所以这里的 ρ 亦可由此线性方程解得。
.
四、李代数求导与扰动模型
4.1李群乘法与李代数加法的关系
为什么要找李群乘法与李代数加法的关系呢？
我们经常会构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前 的估计值。然而，SO(3),SE(3) 上并没有良好定义的加法，它们只是群。如果我们把 T 当成一个普 通矩阵来处理优化，那就必须对它加以约束。而从李代数角度来说，由于李代数由向量组成，具有良好的加法运算。因此，使用李代数解决求导问题的思路分为两种：
- 用李代数表示姿态，然后根据李代数加法来对李代数求导。
- 对李群左乘或右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。
4.1.1 BCH 公式及其近似形式
李群乘积与李代数运算的对应关系由BCH公式给出:
上述的 [ , ] 表示李括号运算。
当 ϕ1 和 ϕ2 为小量时，可以对 BCH 进行线性近似，得到李群乘积对应的李代数的表达式：
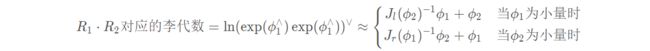
当对一个旋转矩阵 R2（李代数为 ϕ2）左乘一个微小旋转 矩阵 R1（李代数为 ϕ1）时，可以近似地看作，在原有的李代数 ϕ2 上加上了一项 Jl(ϕ2)−1ϕ1。
左乘 BCH 近似雅可比 Jl 事实上就是式 ：
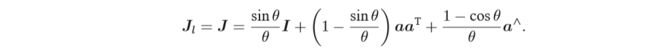
它的逆为：
而右乘雅可比仅需要对自变量取负号即可：
这样，我们就可以谈论李群乘法与李代数加法的关系了。
4.1.2 李群 SO(3) 乘法与李代数 so(3) 加法的关系
对旋转 R (李代数为 ϕ )左乘一个微小旋转 ΔR (李代数为 Δϕ ,得到的旋转李群ΔR · R 对应的李代数为:
反之,李代数加法 (ϕ+Δϕ) 对应的李群元素可表示为:
4.1.3 李群 SE(3) 乘法与李代数 se(3) 加法的关系
李群 SE(3) 乘法与李代数 se(3) 加法的关系:
4.2 SO(3) 上的李代数求导
对空间点p进行旋转,得到Rp,旋转之后点的坐标对旋转的导数可表示为:
对于上式的求导,有两种方式:
- 用李代数 ϕ 表示姿态R，然后根据李代数加法对 ϕ 求导。
- 用李代数 φ 表示微小扰动 ∂R ,然后根据李群左乘对 φ 求导.
其中扰动模型表达式简单，更为实用。
4.2.1 李代数求导
用李代数 ϕ 表示姿态 R ,求导得到
4.2.2 扰动模型（左乘）
另一种求导方式是对 R 进行一次左乘扰动 ∂R，设左乘扰动 ∂R 对应的李代数为 φ 求导,得到
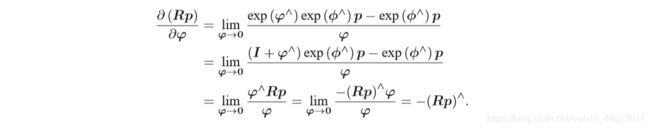
4.3 SE(3) 上的李代数求导
假设某空间点 p 经过一次变换 T（对应李代数为 ξ），得到 TpÀ。现在，给 T 左乘一个扰动 ∆T = exp(δξ∧)，我们设扰动项的李代数为 δξ = [δρ,δϕ]T，那么：
参考文献：
高翔《视觉slam十四讲》
《视觉SLAM十四讲》笔记摘抄
lie group and computer vision : 李群、李代数在计算机视觉中的应用