【总结】CDQ分治总结
前言:
CDQ分治,严格意义上说并不算一种算法,而是一种思想:将问题分为两部分,先解决左半部分,根据左半部分的信息更新右半部分。我的博客主要是借助三位偏序的模型,来介绍这种算法思想。
一维偏序:
一维偏序问题非常经典:其实就是我们常说的排序。
那么,排序有哪些方法?
1、归并排序
2、快排
3、堆排序(借助数据结构)
……
我们常用的大约就是以上三种,如果不记得了请自行复习,这几个算法的思想在之后都会涉及。
二维偏序:
给出N个二元组 (X,Y) ( X , Y ) ,对于每一个二元组 (X,Y) ( X , Y ) ,求满足 Xi<X,Yi<Y X i < X , Y i < Y 的二元组 (Xi,Yi) ( X i , Y i ) 数量。
二维偏序问题也非常容易,一种很简单的思路是:先按照X排序,从小到大依次处理,每次查询完后将当前处理的二元组的Y插入一个堆,每次询问时就查找在堆中小于Y的元素数量。
其实就是一个统计逆序对的过程。
现在拓展一下:
依次插入N个二元组 (X,Y) ( X , Y ) ,对于每一次插入的二元组 (X,Y) ( X , Y ) ,求满足 Xi<X,Yi<Y X i < X , Y i < Y 的二元组 (Xi,Yi) ( X i , Y i ) 数量。
其实这就是三维偏序问题了
三维偏序:
为什么加入一个动态就变成了三位偏序呢?
如果把时间 Ti T i 看做一个维度,那么我们求的其实是满足 Ti<T,Xi<X,Yi<Y T i < T , X i < X , Y i < Y 的三元组 (Ti,Xi,Yi) ( T i , X i , Y i ) 数量
那么三维偏序问题如何解决呢?
回顾一下我们对二维偏序是怎么处理的:我们是将两种处理一维偏序的方法组合起来(排序+堆),那么同理,我们可以尝试将三种排序方式都用上。
注:之后将三元组默认为(X,Y,Z)
首先,我们按照X排序(快排),将原串分为左右两个区间,在两个区间内按照y归并排序,这样一来,我们可以使这两个区间满足如下性质:
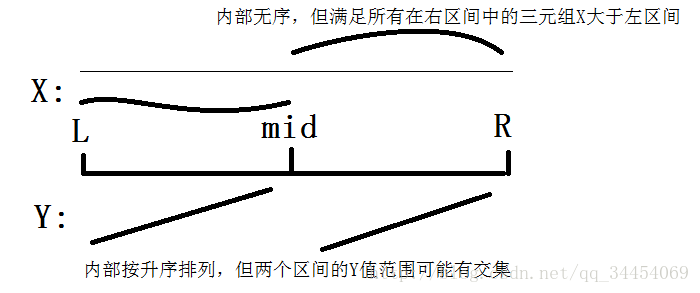
那么处理起来就很显然了:
因为右区间的X一定大于左区间,所以只可能左区间对右区间有贡献。我们在归并排序时,每次存入一个左区间的元素,就将它的Z插入一个堆;每次存入一个右区间的元素,就从堆中找 Zi<Z Z i < Z 的数量。
最后来分析一下时间复杂度:快排嵌套堆 (nlog2n) ( n l o g 2 n ) +归并排序 (nlogn) ( n l o g n ) -> nlog2n n l o g 2 n
这么看,似乎复杂度和树套树没有区别,但其实在实际运行中,由于快排的常数小于许多 nlogn n l o g n 级数据结构的常数,所以CDQ分治的速度一般优于树套树,一个更大的优点是:CDQ分治的代码通常比树套树短很多,在考场上更容易实现。
但是CDQ分治也有一些致命的弱点:必须离线操作。如果题目强制在线,那么除非出题人故意恶搞,否则基本就不可能是CDQ分治了。
网上很多对CDQ分治算法的讲解,但大部分都是以货币兑换作为模板的。我的讲解是按照LJH大佬的课件,通过三位偏序问题来讲解的,因此,可能与网上的其他的CDQ分治算法讲解有所冲突。
模板题:BZOJ3295动态逆序对(可以尝试用树套树过一次…反正我是卡的时限…10000多毫秒过的)
#includex;i++)
add(p[i].y,1);
ans[p[j].t]+=(i-l)-que(p[j].y);
}
i--;
for(;i>=l;i--)
add(p[i].y,-1);
i=mid;
for(j=r;j>mid;j--){
for(;i>=l&&p[i].x>p[j].x;i--)
add(p[i].y,1);
ans[p[j].t]+=que(p[j].y);
}
i++;
for(;i<=mid;i++)
add(p[i].y,-1);
cdq(l,mid);
cdq(mid+1,r);
}
int main(){
int b,cnt=0;
SF("%d%d",&n,&m);
for(int i=1;i<=n;i++)
SF("%d",&a[i]);
for(int i=1;i<=m;i++){
SF("%d",&b);
t[b]=i;
}
for(int i=1;i<=n;i++){
if(t[a[i]])
p[i]=node(n-t[a[i]]+1,i,a[i]);
else
p[i]=node(++cnt,i,a[i]);
}
cdq(1,n);
for(int i=2;i<=n;i++)
ans[i]+=ans[i-1];
for(int i=n;i>n-m;i--)
PF("%lld\n",ans[i]);
}