阶乘除法 —— legendre 勒让德定理
题目描述
输入
第一行三个整数,n,m和T。
第二行n个数,第i个数表示ai。
第三行m个数,第i个数表示bi。
输出
输出一个数,答案对T取余数的结果。
样例输入
3 2 998244353 2 2 6 3 3
样例输出
80
具体分析
由于这里有阶乘,还有mod T , 所以可以考虑legendre定理
legendre定理:在n!标准分解式(质因数分解)中,素数p的最高指数为![]()
通过它,我们就能把原式分解为:
这里我们先不管maxx(反正是个范围)
这时我们考虑桶排序
用一个c数组来当桶存a[i],原式就化简为:
这里我们先不管maxx和pn(反正还是个范围)
其实我们发现下去整这里是有阶段性的
其实就是 2/2 = 3/2下去整
所以我们可以去枚举![]()
于是:
这时i是![]() 的值
的值
但是这样是四重循环,我们其实可以优化,还记得我们是用桶来做的吗,我们可以用桶做前缀和,就像这样:
for( int i = 1 ; i <= n ; i ++ ){
scanf( "%d" , &x );
s[x] ++;
maxx = max( x , maxx );
}
for( int i = 1 ; i <= maxx ; i ++ )
s[i] = s[i-1] + s[i];然后第四重循环就变成了s[(i+1)*p∧k-1] - s[i*p∧k-1]。
然后我们用质因数分解做,用一个a[]数组存
这里不知道怎么描述,大家还是看代码吧
代码
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 1e5 + 2;
bool vis[MAXN];
int n , m , x , maxx;
long long s[MAXN] ;
int pn , prime[MAXN];
long long t , a[MAXN];//这里最好都开long long ,自己因为这个错了n遍
void pr( ){//用欧拉筛求素数
for( int i = 2 ; i <= MAXN - 2 ; i ++ ){
if( vis[i] == 0 ){
prime[++pn] = i;
}
for( int j = 1 ; j <= pn && 1ll * i * prime[j] <= MAXN - 2 ; j ++ ){
vis[i*prime[j]] = 1;
if( i % prime[j] == 0 ) break;
}
}
}
long long qpow( long long x , long long y ){
long long sum = 1;
while( y ){
if( y % 2 )
sum = sum * x % t;
x = x * x % t;
y /= 2;
}
return sum;
}
int main(){
pr();
scanf( "%d%d%lld" , &n , &m , &t );
for( int i = 1 ; i <= n ; i ++ ){
scanf( "%d" , &x );
s[x] ++;
maxx = max( x , maxx );//算一个最大值,这样可以节省时间,不用每次都是MAXN
}
for( int i = 1 ; i <= maxx ; i ++ )
s[i] = s[i-1] + s[i];
for( int i = 1 ; i <= pn && prime[i] <= maxx ; i ++ ){//枚举质数
for( long long j = prime[i] ; j <= maxx ; j *= prime[i] )//这里是枚举p的k次方
for( long long k = 1 ; k * j <= maxx ; k ++ ){//枚举下去整的值
long long l = k * j , c = min( 1ll * maxx , 1ll * ( l + j - 1 ) );
a[i] += ( s[c] - s[l-1] ) * k;//如果这里已经大于maxx,那么就取maxx,否则数组越界
}
}
memset( s , 0 , sizeof( s ) );
maxx = 0;
for( int i = 1 ; i <= m ; i ++ ){
scanf( "%d" , &x );
s[x] ++;
maxx = max( maxx , x );
}
for( int i = 1 ; i <= maxx ; i ++ )
s[i] = s[i-1] + s[i];
for( int i = 1 ; i <= pn && prime[i] <= maxx ; i ++ ){//因为是除法,我们可以当做它是
for( long long j = prime[i] ; j <= maxx ; j *= prime[i] )//被抵消,所以a[i]是减
for( long long k = 1 ; k * j <= maxx ; k ++ ){
long long l = k * j , c = min( 1ll * maxx , l + j - 1 );
a[i] -= ( s[c] - s[l-1] ) * k;
}
}
long long ans = 1;
for( int i = 1 ; i <= pn ; i ++ ){
ans = ans * qpow( prime[i] , a[i] ) % t;//快速幂,别忘了模t
}
printf( "%lld" , ans );
return 0;
}
![\sum_{i=1}^{i <= n} \sum_{p}^{}\sum \sum_{k}^{maxx} \left \lfloor a[i]/p^{k} \right \rfloor](http://img.e-com-net.com/image/info8/adc37bd1e027499f849afa96d5499b50.gif)
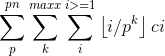
![\sum_{p}^{p <=pn} \sum_{k}^{k<=maxx}\sum_{i} i * \sum \sum_{j = i * p^{k}}^{(i+1) * p^{k}-1} c[j]](http://img.e-com-net.com/image/info8/8fd0f5d7a9964028b7a409c559fdcadb.gif)