POJ-1067 取石子游戏 解题报告

Description

有两堆石子，数量任意，可以不同。游戏开始由两个人轮流取石子。游戏规定，每次有两种不同的取法，一是可以在任意的一堆中取走任意多的石子；二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目，如果轮到你先取，假设双方都采取最好的策略，问最后你是胜者还是败者。

Input

输入包含若干行，表示若干种石子的初始情况，其中每一行包含两个非负整数a和b，表示两堆石子的数目，a和b都不大于1,000,000,000。

Output

输出对应也有若干行，每行包含一个数字1或0，如果最后你是胜者，则为1，反之，则为0。

Sample Input

2 1
8 4
4 7

Sample Output

0
1

       题目链接：http://poj.org/problem?id=1067

       解法类型：威佐夫博奕

       解题思路：就是一个经典的威作福博弈，知道公式就很水了。现给出我看到的一个很牛叉的证明：

• 简单分析一下，容易知道两堆石头地位是一样的，我们用余下的石子数(a,b)来表示状态，并画在平面直角坐标系上。

  用之前的定理： 有限个结点的无回路有向图有唯一的核  中所述的方法寻找必败态。先标出(0,0)，然后划去所有(0,k),(k,0),(k,k)的格点；然后找y=x上方未被划去的格点，标出(1,2)，然后划去(1,k),(k,2),(1+k,2+k)，同时标出对称点(2,1)，划去(2,k),(1,k),(2+k,1+k)；然后在未被划去的点中在y=x上方再找出(3,5)。。。按照这样的方法做下去，如果只列出a<=b的必败态的话，前面的一些是(0,0),(1,2),(3,5),(4,7),(6,10),…

  

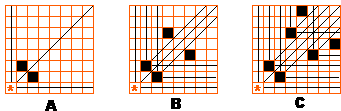
  接下来就是找规律的过程了，忽略(0,0)，记第n组必败态为(a[n],b[n])

  命题一：a[n+1]=前n组必败态中未出现过的最小正整数

  [分析]：如果a[n+1]不是未出现的数中最小的，那么可以从a[n+1]的状态走到一个使a[n+1]更小的状态，和我们的寻找方法矛盾。

  命题二：b[n]=a[n]+n

  [分析]：归纳法：若前k个必败态分别为 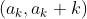，下证：第k+1个必败态为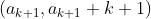

  从该第k+1个必败态出发，一共可能走向三类状态，从左边堆拿走一些，从右边堆拿走一些，或者从两堆中拿走一些．下面证明这三类都是胜态．

  情况一：由命题一，任意一个比a[k+1]小的数都在之前的必败态中出现过，一旦把左边堆拿少了，我们只要再拿成那个数相应的必败态即可。

  情况二（从右边堆拿走不太多）：这使得两堆之间的差变小了，比如拿成了 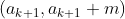，则可再拿成 ；

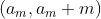  情况二（从右边堆拿走很多）：使得右边一堆比左边一堆更少，这时类似于情况一，比如拿成了 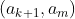(其中a[m] ；

  情况三：比如拿成 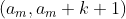，则可再拿成 ．

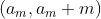  综上所述，任何从 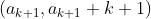出发走向的状态都可以走回核中．故原命题成立．

  以上两个命题对于确定(a[n],b[n])是完备的了，给定(0,0)然后按照这两个命题，就可以写出(1,2),(3,5),(4,7),…

  这样我们得到了这个数列的递推式，以下我们把这两个命题当成是(a[n],b[n])的定义。

  先证明两个性质：

  性质一：核中的a[n],b[n]遍历所有正整数。

  [分析]：由命题一，二可得a[n],b[n]是递增的，且由a[n]的定义显然。

  性质二：A={a[n]:n=1,2,3,…},B={b[n]:n=1,2,3,…}，则集合A,B不交。

  [分析]：由核是内固集，显然。

  看到这里大家有没有想到Beatty序列呢，实际上a[n]和b[n]就是一个Beatty序列。

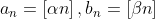  ，有 ，解方程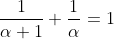

  得 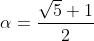，到此，我们找到了该必败态的通项公式。

  实际上这组Beatty序列还有一些别的性质，比如当一个数是Fibonacci数的时候，另一个数也是Fibonacci数；而且两者的比值也越来越接近黄金比，这些性质在得到通项公式之后不难证明。

  总的来说，这个问题给我们了哪些启示呢？首先用定理所说的方法找核，然后给出核的规律（递推，或是通项）并且证明。最后附上一张对应的必败态图.

  PS：用图来表示博弈过程，好想法啊。~

  
  

  算法实现：

  //STATUS:C++_AC_32MS_172k
  #include
  #include
  const double x=((sqrt(5.0)+1)/2);
  int main()
  {
  //	freopen("in.txt","r",stdin);
  	int a,b,k,ta;
  	while(~scanf("%d%d",&a,&b))
  	{
  		if(a>b){int t=a;a=b,b=t;}
  		k=b-a;
  		ta=(int)floor(k*x);
  		printf("%d\n",ta==a?0:1);
  	}
  	return 0;
  }