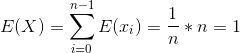【leetcode系列】【算法】2020春季全国编程大赛-团队赛（更新第五题解题思路和代码）
写在前面：
本次题感觉总体都有ACM的味道了，个人感觉难度极高...
强烈建议自己先考虑一下，然后再看题解
题目一：
题目链接： https://leetcode-cn.com/contest/season/2020-spring/problems/qi-wang-ge-shu-tong-ji/
解题思路：
通过分析题目发现，不同分数的简历之间是不会互相影响的，所以原问题等同于n个数字全排列之后，有多少元素还在原位置
设这个随机变量为
，对于
，如果第i个元素还在原位，则
，否则
对于每一个元素，随机排序后还在原位的概率为
。由于期望的可加性，可以得到如下的式子：
由结果可知，
最终与n无关，所以我们只需要计算有多少个不重复的数字就可以了
利用hash的性质，统计有多少不相同的数字，再返回hash表中key的个数
时间复杂度：O(N)
代码实现：
class Solution:
def expectNumber(self, scores: List[int]) -> int:
return len(set(scores))
题目二：
题目链接： https://leetcode-cn.com/contest/season/2020-spring/problems/xiao-zhang-shua-ti-ji-hua/
解题思路：
二分查找
初始的left = 0, right = 所有时间之和，然后开始二分查找
每次取mid之后，mid是每一天的做题时间。然后根据mid，判断当前被分成几天完成
如果大于m天，说明需要调大mid，则更新left = mid + 1
如果小于等于m天，说明需要调小mid，则更新right = mid
关于求助功能的体现，在代码注释中有详细解释
代码实现：
class Solution:
def minTime(self, time: List[int], m: int) -> int:
def check(mid, time, m):
# 根据当前mid天数,计算出需要的总天数
use_day = 1
# 当前序列需要使用的天数
total_time = 0
# 当前序列中的最大耗时
max_time = time[0]
for t in time[1:]:
# 因为是可以求助的,所以可以每组中多一道题
# 所以从1开始遍历,并且更新当前题组total_time时,排除掉耗时最高的一个
if total_time + min(max_time, t) <= mid:
# 更新当前题组的总耗时,加上当前值和最大值中更小的一个
# 最终达到目的：题组中的最大耗时,使用求助功能解答
total_time += min(max_time, t)
max_time = max(max_time, t)
else:
# 排除掉最大耗时,当前题组也超过mid限制的天数了
# 此时更新当前需要天数use_day += 1
# 并重置题组所需天数和最高耗时
use_day += 1
total_time = 0
max_time = t
return use_day <= m
# 初始化最小值为0,最大值为时间总和
left, right = 0, sum(time)
while left < right:
mid = (left + right) >> 1
if check(mid, time, m):
# 总耗时天数 <= m，想要增大总耗时,通过调小right调小mid
right = mid
else:
# 总耗时天数 > m，想要减小总耗时,通过增大left增大mid
left = mid + 1
return left
题目三：
题目链接： https://leetcode-cn.com/contest/season/2020-spring/problems/xun-bao/
解题思路：
事实上，我们的走法只有这么几种：
- 从S走向O，取石头
- 从O走向M，踩机关
- 从M走向O，再次取石头
- 从M走向T，所有机关都已经触发，走向终点
BFS：
对于所有的S、M、O和T，不论我们做什么操作（触发机关、搬运石头），互相之间的连通性是不会变化的
所以在开始的时候，对每一个特殊点都进行一次BFS，搜索当前点到其他点的最短距离，之后就不需要再去搜索了
状态压缩DP：
在最开始，我们一定是从S点开始，经过一个O点搬一块石头，再到达一个M点触发机关。所以我们先枚举S通过某个O到达每一个M的最短距离（S -> O -> M），这样我们就首先得到了按照游戏规则的S到每一个M的最短距离
接下来，按照游戏规则，我们需要从某个M出发，到达O搬运一块石头，再到达其他未出发机关的M点（M -> O -> M'），和计算S -> O -> M的逻辑相同，我们需要枚举出所有M -> O -> M'的最短距离，就得到了按照游戏规则的每一个M到达其他M的最短距离
而M到T的距离，之前在BFS的时候已经计算出来了
这样，我们就将已知条件转换为了：
- 按照游戏规则，S到达每一个M的最短距离
- 按照游戏规则，M到达每一个M‘的最短距离
- 每一个M到达T的最短距离
这样就是一个经典的状压DP问题了
令dp[s][i]表示在第i个机关，总触发状态为s的最小步数（s是一个状态的bitmap），那么枚举当前没有触发的机关j，状态转移公式为：
![dp[s|(1<<j)][j]=min(dp[s|(1<<j)][j],dp[s][i]+minDistance(i,j))](http://img.e-com-net.com/image/info8/dd259cb94986456e83bab1084ad8e9f0.gif){kind=small}
其中
为之前预处理出的所有特殊点之间的最小距离
复杂度分析：
- BFS时间复杂度
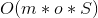，其中m为M点的数目，o为O点的数目，S为迷宫面积 - dp时间复杂度为
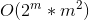
代码实现：
import queue
class Solution:
def bfs(self, maze):
"""
以迷宫maze中的每个特殊点为中心,BFS搜索到其他所有特殊点的最近距离
Args:
maze : 原始迷宫信息
Returns:
total_dis_info : 按照special_point中的顺序,保存每个点到其余点的最近距离.如果要获取第i个点到第j个点的最近距离,可以直接使用total_dis_info[i][j]获取
tag : 保存每个类型的点,在special_point中的索引值,同时也是total_dis_info中的索引值
"""
# 迷宫的高和宽
height, width = len(maze), len(maze[0])
# 特殊点位置信息
special_point = []
for i in range(height):
for j in range(width):
if maze[i][j] in ['S', 'T', 'M', 'O']:
special_point.append((i, j, maze[i][j]))
# 按照special_point中的顺序,保存每个点到其余点的最近距离
# 如果要获取第i个点到第j个点的最近距离,可以直接使用total_dis_info[i][j]获取
total_dis_info = []
# 保存每个类型的点,在special_point中的索引值
# 这个索引值,同时也是在total_dis_info中的索引值
tag = collections.defaultdict(list)
# 以每个特殊点为中心，开始BFS搜索其他特殊点的最短距离
for idx, (x, y, point_type) in enumerate(special_point):
q = queue.Queue()
dis = [[float('inf') for i in range(width)] for j in range(height)]
dis[x][y] = 0
q.put((x, y))
while not q.empty():
curr_x, curr_y = q.get()
# BFS时搜索的的方向
# 按照数组顺序，分别为：向下、向右、向上、向左
for x_move, y_move in [[0, 1], [1, 0], [0, -1], [-1, 0]]:
nxt_x = curr_x + x_move
nxt_y = curr_y + y_move
if nxt_x < 0 or nxt_x >= height or nxt_y < 0 or nxt_y >= width:
# 超出边界
continue
elif maze[nxt_x][nxt_y] == '#':
# 不可通行
continue
if dis[nxt_x][nxt_y] > dis[curr_x][curr_y] + 1:
# 如果nxt_x,nxt_y的位置之前没搜索到,当前距离应该是无穷大
# 或者之前搜索到nxt_x,nxt_y的位置,并且距离比本次搜索的距离要大
# 则更新nxt_x,nxt_y和原始x,y的最近距离为当前距离 + 1
# 并将nxt_x,nxt_y加入队列，继续搜索
dis[nxt_x][nxt_y] = dis[curr_x][curr_y] + 1
q.put((nxt_x, nxt_y))
# 当前点到其他所有特殊点,按照保存在special_point中的顺序的最小距离
curr_dis_info = []
for i, j, _ in special_point:
curr_dis_info.append(dis[i][j])
#加入到结果集中
total_dis_info.append(curr_dis_info)
tag[point_type].append(idx)
return total_dis_info, tag
def state_compression_dp(self, total_dis_info, tag):
"""
状态压缩DP处理
Args:
total_dis_info : BFS的距离信息
tag : 每个特殊点的索引序列
Returns:
最终步数结果
"""
m_num = len(tag['M'])
o_num = len(tag['O'])
s_idx = tag['S'][0]
t_idx = tag['T'][0]
dp = [[float('inf') for i in range(m_num)] for j in range(1 << m_num)]
# 处理S -> O -> M的最短距离
for i in range(m_num):
m_idx = tag['M'][i]
# s移位后,dp[s][i]表示的是每个M到自己的距离
self_idx = 1 << i
for j in range(o_num):
o_idx = tag['O'][j]
# 更新每个M到自己的距离,为S开始,经过每个O,到自己的最小距离
dp[self_idx][i] = min(dp[self_idx][i], total_dis_info[s_idx][o_idx] + total_dis_info[o_idx][m_idx])
# 预处理M -> O -> M的距离
m_2_m_dis = [[float('inf') for i in range(m_num)] for j in range(m_num)]
for i in range(m_num):
m_idx1 = tag['M'][i]
for j in range(m_num):
m_idx2 = tag['M'][j]
for k in range(o_num):
o_idx = tag['O'][k]
# 获取每个M,经过O,到达其他M的最短距离
m_2_m_dis[i][j] = min(m_2_m_dis[i][j], total_dis_info[m_idx1][o_idx] + total_dis_info[o_idx][m_idx2])
# 状态压缩DP
for s in range(1 << m_num):
for j in range(m_num):
if s & (1 << j) == 0:
continue
for k in range(m_num):
if s & (1 << k) != 0:
continue
ns = s | (1 << k)
dp[ns][k] = min(dp[ns][k], dp[s][j] + m_2_m_dis[j][k])
ans = float('inf')
fs = (1 << m_num) - 1
for j in range(m_num):
m_idx = tag['M'][j]
ans = min(ans, dp[fs][j] + total_dis_info[m_idx][t_idx])
return -1 if ans == float('inf') else ans
def minimalSteps(self, maze: List[str]) -> int:
"""
根据输入的迷宫，计算一共需要多少步，才能在触发所有机关后，从起点走向终点
Args:
maze : m * n的迷宫矩阵
Returns:
需要的步数
"""
total_dis_info, tag = self.bfs(maze)
if 'M' not in tag:
# 如果没有机关,则直接返回起点到终点的最近距离
# 因为S和T有且只有1个,所以直接获取相应的第一个
s_idx = tag['S'][0]
t_idx = tag['T'][0]
# 如果起点无法到达终点,则返回-1; 否则返回起点到终点的最近距离total_dis_info[s_idx][t_idx]
return -1 if float('inf') == total_dis_info[s_idx][t_idx] else total_dis_info[s_idx][t_idx]
return self.state_compression_dp(total_dis_info, tag)
题目四：
题目链接： https://leetcode-cn.com/contest/season/2020-spring/problems/qie-fen-shu-zu/
解题思路：
假设![f[i]](http://img.e-com-net.com/image/info8/e3327f74e15944e98fb228dd023a3bec.gif)
表示在将i这个质数添加到数组中后，数组的最少分组是几个
比如对于数组[2, 5, 3, 6]，在从前向后遍历时，对f的更新如下：
- 遍历到数字2，此时只有1个数字，只能划分为1个子数组，所以f[2] = 1
- 遍历到数字5，此时有2个数字，但是最大公约数为1，需要划分为2个数组，所以f[5] = 2
- 遍历到数字3，此时有3个数字，但是所有数字之间的最大公约数都为1，需要划分为3个数组，所以f[3] = 3
- 遍历到数字6，此时有4个数字，先获取6的最小质因数2，发现与2的最大公约数为2 > 1，可以与2构成一个符合条件的子数组，所以f[6] = 1，并对6除以最小质因数2进行再次循环处理，处理的数字为6 / 2 = 3
- 处理3时，发现与前面的数字3有最大公约数 = 3 > 1，可以与3构成一个符合条件的子数组，当与3构成子数组时，分为2个子数组：[2, 5], [3, 6]，所以更新f[3] = 2；但是之前使用2为质因数时，最小子数组个数为1，所以当前的最小子数组个数仍为1
代码实现：
class Solution:
def __init__(self):
# 事先对小于10^6数字进行预处理,计算所有数字的最小质因子,方便后续处理
# 放在init中初始化,会导致在leetcode的性能测试中超时
# 如果为了通过leetcode测试,需要将init逻辑放在类外,将此部分时间放到import中,不会占用测试case的耗时
# 但是为了代码结构合理,此处放在了init中进行初始化
max_num = pow(10, 6)
self.rec = [1] * (max_num + 1)
num = 2
while num <= max_num:
times = num
while times * num <= max_num:
# 这段逻辑的意思,是说从小到大的乘上去
# num当前的值,就是第一次遍历到的数字的最小质因数
# times从当前数字开始,因为小于当前数字的倍数,已经在之前遍历过了
if self.rec[times * num] == 1:
self.rec[times * num] = num
times += 1
num += 1
while num <= max_num:
# 目的为找到下一个没有设置最小质因数的数字
if self.rec[num] == 1:
break
num += 1
def splitArray(self, nums: List[int]) -> int:
"""
对输入的数组nums进行子数组划分,要求为每个子数组的第一个和最后一个数字最大公约数大于1
Args:
nums : 需要切分的原始数组
Returns:
划分的子数组最小个数
"""
prime_factor = {}
n = len(nums)
curr_num = nums[0]
# 先对第一个数字进行质因数分解,并把分解结果加入到prime_factor中
while True:
if self.rec[curr_num] == 1:
prime_factor[curr_num] = 1
break
prime_factor[self.rec[curr_num]] = 1
curr_num //= self.rec[curr_num]
# 初始化最小步数,因为最少分为1个数组,所以初始化为1
min_step = 1
for curr_num in nums[1:]:
# 这段循环的主要逻辑如下：
# 对每个数字进行质因数分解,并判断分解出的质因数,是否在前面的数字中出现过
# 如果没出现,则说明需要新增一个子数组
# 如果出现过,说明当前数字可以与前面的某个数字构成符合条件的子数组
# 这个时候,就与前面的数字进行合并,可能导致总子数组个数不变,也有可能减小
# 比如对于数组[2, 3, 6]
# 遍历到3时,子数组个数为2; 当遍历到6时,发现和数字2有大于1的公约数,所以就将子数组个数更新为1
curr_min_step = float('inf')
while True:
if self.rec[curr_num] == 1:
# 如果无法继续做质因数分解,则更新当前curr_num的质因数个数
prime_factor[curr_num] = min(prime_factor.get(curr_num, float('inf')), min_step + 1)
curr_min_step = min(curr_min_step, prime_factor[curr_num])
break
# 判断当前curr_num是否能够和之前的数字构成符合条件的子数组
# 如果可以,则使用curr_num对应的之前的子数组
# 如果不可以,则说明curr_num需要新加子数组,更新curr_num位置的子数组个数为当前的最小字数字个数 + 1
prime_factor[self.rec[curr_num]] = min(prime_factor.get(self.rec[curr_num], float('inf')), min_step + 1)
curr_min_step = min(curr_min_step, prime_factor[self.rec[curr_num]])
curr_num //= self.rec[curr_num]
min_step = curr_min_step
return min_step
题目五：
（上图：A->B->C 右转； 下图：D->E->F 左转）
题目链接： https://leetcode-cn.com/contest/season/2020-spring/problems/you-le-yuan-de-mi-gong/
解题思路：
这道题其实比较简单，不过需要事先了解一下叉积的性质：
- 如果
，说明
在
的左侧
- 如果
，说明
如果要求下个转向关系为左转，那么本次找到最右边的一个点，则剩余的点全部都是左转；如果要求下个转向关系为右转，那么本次找到最左边的一个点，则剩余的点全部都是右转
代码实现：
class Solution:
def sub(self, a: List[int], b: List[int]):
"""
根据两个点，计算其向量表示
Args:
a : 向量起点
b : 向量终点
Returns:
起点a到终点b的向量
"""
return [a[0] - b[0], a[1] - b[1]]
def cross(self, a: List[int], b: List[int]):
"""
计算两个向量的叉积
Args:
a : 第一个向量
b : 第二个向量
Returns:
向量叉积
如果 > 0, 说明b在a的左边
如果 < 0，说明b在a的右边
"""
return a[0] * b[1] - a[1] * b[0]
def get_next_point(self, turn_type, point_num, points, used, last_idx):
"""
根据当前转向类型和上个点位置,计算下个点的位置
Args:
turn_type : 要求的转向类型
point_num : 总点数
points : 点序列
used : 对应的点是否已被使用
last_idx : 上一个选中点的索引值
Returns:
下个点的索引值
"""
target_idx = -1
for i in range(point_num):
if used[i]:
# 当前点已经被使用
continue
elif target_idx == -1:
# 找到的第一个可用的点
target_idx = i
continue
# 根据当前选中的点，和上个选中的点，计算其向量标识
curr_vector = self.sub(points[target_idx], points[last_idx])
# 根据当前遍历的点，和上个选中的点，计算其向量标识
next_vector = self.sub(points[i], points[last_idx])
# 计算两个向量的叉积
curr_cross = self.cross(curr_vector, next_vector)
if turn_type == 'L' and curr_cross < 0:
# 说明next_vector在curr_vector右边
# 因为下个转向类型为左转，想要找到当前最右边的点
# 所以更新下个点的索引值为当前遍历索引
target_idx = i
elif turn_type == 'R' and curr_cross > 0:
# 说明next_vector在curr_vector左边
# 因为下个转向类型为右转，想要找到当前最左边的点
# 所以更新下个点的索引值为当前遍历索引
target_idx = i
return target_idx
def visitOrder(self, points: List[List[int]], direction: str) -> List[int]:
"""
根据输入的points点序列，找到符合direction转向序列要求的结果集
Args:
points : 输入的点序列
direction : 输入的转向序列
Returns:
符合要求的点索引序列
"""
n = len(points)
# 记录已经用过的点
# 使用额外数组记录，而不是删除原先数组中的元素，是因为删除后，不管是python的list，还是c++的vector，都需要把后面的元素依次向前移一个
# 这样会使得效率下降，最差情况下，每次都是删除第一个，将后面所有元素都向前移动
used = [False] * n
# 结果序列
res = []
# 从最左边的点开始,主要是从某一边开始,最右边、最下边、最上边的点也可以
start = 0
for i in range(n):
if points[i][0] < points[start][0]:
start = i
# 更新起点状态，并加入到结果集
used[start] = True
res.append(start)
# 开始寻找符合条件的点序列
for i in direction:
# 获取下个点索引值
next_idx = self.get_next_point(i, n, points, used, start)
# 更新下个点状态，并加入到结果集
used[next_idx] = True
res.append(next_idx)
start = next_idx
# 将最后一个未使用过的点放入到结果集中
for i in range(n):
if not used[i]:
res.append(i)
break
return res
题目六：
题目链接： https://leetcode-cn.com/contest/season/2020-spring/problems/you-le-yuan-de-you-lan-ji-hua/