Matlab知识点（六）

使用Matlab处理积分问题

最值问题
在Matlab 中只有求极（或最）小值命令的函数．若要求函数 f ( x)在( x1, x2) 内的极（或最）大值，可转化为求− f (x)在( x1, x2) 内的极（或最）小值．求极（或最）小值点和极（或最）小值的调用格式是： [x,fual]=fminbnd(‘fun’,x1,x2)

[xmin,fmin]=fminbnd('1-3*x-x^2',-10,9);  % 求f(x)的最小值点和最值
[xmax,zmin]= fminbnd('-1+3*x+x^2',-10,9);  %转化为-f(x)的最小值和最小值点
fmax = -zmin;%-(-f(x))的最大值
xmin,fmin,xmax,fmax

输出的结果是：
xmin = 9.0000
fmin = -106.9992
xmax = -1.5000
fmax =3.2500

[xmin,fmin]=fminbnd('2*exp(-x)*sin(x)',2,5)

xmin =3.9270
fmin = -0.0279

一元函数的不定积分

1、调用格式一： int(‘f(x)’,‘x’)

int(x^2*cos(x),'x')

运行结果：ans = sin(x)(x^2 - 2) + 2x*cos(x)

2、调用格式二：
syms x % 声明变量
int(f(x),x)

syms x a; % 中间没有分隔符
int(a^2*exp(x)*sin(2*x),x)

结果是：ans = -(a^2exp(x)(2cos(2x) - sin(2*x)))/5

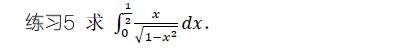
int(x/sqrt(1-x^2),'x',0,1/2)  % 函数不需要引号，自变量需要

结果是：ans = 1 - 3^(1/2)/2

syms x;
int(1/(1+x^2),x,-inf,inf)

结果是：ans = pi

syms x y;
int(int(x^2+y^2,x,-1,2),y,0,4)

结果是： ans = 76

syms t
int(sqrt(1-t^2),'t',a,x)

ans = asin(x)/2 - asin(a)/2 - (a*(1 - a²⁾(1/2))/2 + (x*(1 - x²⁾(1/2))/2

syms t
int(abs(t-1),t,-1,2)

结果是：ans = 5/2