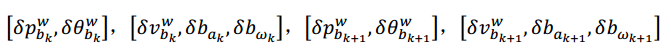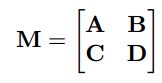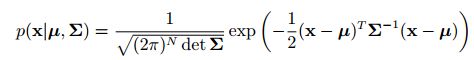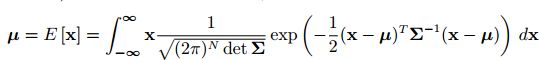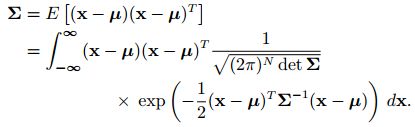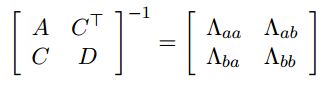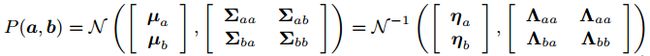VINS-Mono——后端优化
文章目录
- 状态向量
- 代价函数(Minimize residuals from all sensors)
- IMU 测量约束
- IMU 测量残差
- 优化变量
- 雅克比矩阵
- 协方差矩阵
- 视觉测量残差
- 重投影误差(视觉测量残差)
- 优化变量
- 雅克比矩阵
- 协方差矩阵
- 边缘化和FEJ
- 舒尔补定义
- 高斯分布与边缘化
- 多元高斯分布
- 联合高斯分布的分解
- 协方差矩阵+均值
- 信息矩阵+信息矢量
- 总结
状态向量
VIO 紧耦合方案的主要思路就是通过将基于视觉构造的残差项和基于 IMU 构造的残差项放在一起构造成一个联合优化的问题,整个优化问题的最优解即可认为是比较准确的状态估计。
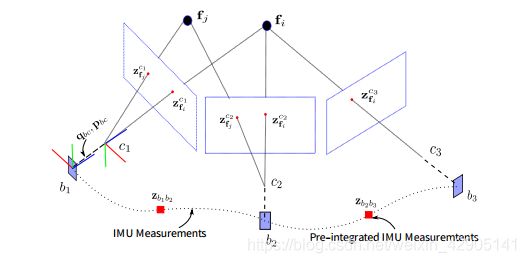
为了限制优化变量的数目, VINS-Mono 采用了滑动窗口的形式, 滑动窗口中的全状态量包括滑动窗口内的n+1个关键帧时刻 IMU 坐标系的位置、姿态、姿态(旋转)、加速度计偏置、陀螺仪偏置, Camera 到 IMU 的外参, m +1个 3D 路标点的逆深度:

优化过程中的误差状态量为:
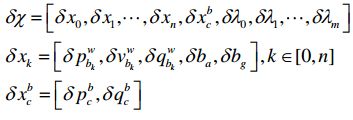
代价函数(Minimize residuals from all sensors)
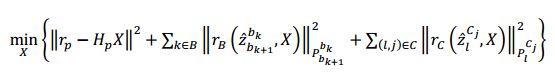
其中 P b k + 1 b k P^{b_k}_{b_{k+1}} Pbk+1bk为 IMU 预积分噪声项的协方差矩阵, P l c j P^{c_j}_l Plcj为视觉观测噪声的协方差矩阵。
三个残差项即误差项分别为边缘化的先验信息、 IMU 测量残差、视觉的重投影残差。三种残差都是用马氏距离表示。
根据高斯牛顿法求优化过程中最为核心的增量方程,以 IMU 测量残差为例,先将 r b ( z ^ b k + 1 b k , χ ) r_{b}(\hat z^{b_k}_{b_{k+1}},\chi ) rb(z^bk+1bk,χ)进行一阶泰勒展开

其中 H b k + 1 b k H^{b_k}_{b_{k+1}} Hbk+1bk是雅可比矩阵
等号右边关于 δ x \delta x δx的导数,并令其为 0,得到增量方程:
![]()
那么可以写出函数对应的增量方程:

增量方程可进一步简化为:
![]()
其中 ∧ p \wedge _p ∧p, ∧ B \wedge _B ∧B, ∧ C \wedge _C ∧C为(近似的) Hessian 矩阵,上述方程称之为增量方程。
IMU 测量约束
IMU 测量残差
根据上面的 IMU 预积分,得到 IMU 预积分残差(估计值 - 测量值)

其中 [ q ] x y z [q]_{xyz} [q]xyz表示提取四元数q的虚部, [ α ^ b k + 1 b k , β ^ b k + 1 b k , γ ^ b k + 1 b k ] T [\hat \alpha^{b_k}_{b_{k+1}},\hat \beta ^{b_k}_{b_{k+1}},\hat \gamma ^{b_k}_{b_{k+1}}]^T [α^bk+1bk,β^bk+1bk,γ^bk+1bk]T为关键帧 b k b_k bk和关键帧 b k + 1 b_{k+1} bk+1时间间隔内,仅仅使用含有噪声的加速度计和陀螺仪数据计算的预积分 IMU 测量项, δ θ b k + 1 b k \delta \theta^{b_k}_{b_{k+1}} δθbk+1bk是四元数误差的三维表示。
优化变量
雅克比矩阵
高斯迭代优化过程中会用到 IMU 测量残差对状态量的雅克比矩阵,但此处我们是对误差状
态量求偏导
- 对k时刻 [ δ p b k w , δ θ b k w ] [\delta p^w_{b_k},\delta \theta^w_{b_k}] [δpbkw,δθbkw]求偏导数
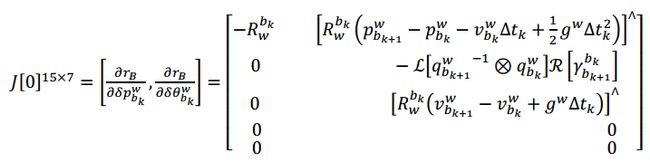
- 对k时刻 [ δ v b k w , δ b a k , δ θ b w k ] [\delta v^w_{b_k},\delta b_{a_k},\delta \theta b_{w_{k}}] [δvbkw,δbak,δθbwk]求偏导数

- 对k时刻 [ δ p b k + 1 w , δ θ b k + 1 w ] [\delta p^w_{b_{k+1}},\delta \theta^w_{b_{k+1}}] [δpbk+1w,δθbk+1w]求偏导数
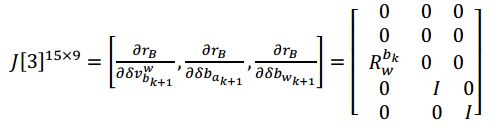
- 对k时刻 [ δ v b k + 1 w , δ b a k + 1 , δ θ b w k + 1 ] [\delta v^w_{b_{k+1}},\delta b_{a_{k+1}},\delta \theta b_{w_{k+1}}] [δvbk+1w,δbak+1,δθbwk+1]求偏导数
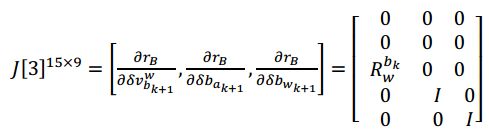
上面公式在代码中对应: class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9>对于 Evaluate 输入 double const *const *parameters, parameters[0], parameters[1], parameters[2],parameters[3]分别对应 4 个输入参数, 它们的长度依次是 7,9,7,9, 分别对应 4 个优化变量的参数块。
代码 IMUFactor::Evaluate()中 residual 还乘以一个信息矩阵 sqrt_info, 这是因为真正的优化项其实是 Mahalanobis 距离: d = r T P − 1 r d=r^TP^{−1}r d=rTP−1r,P 是协方差,又因为 Ceres 只接受最小二乘优化, 也就是 m i n ( e T e ) min(e^Te) min(eTe)所以把?−1做 LLT 分解, 即 L L T = P − 1 LL^T=P^{-1} LLT=P−1, 则有:

令 r ′ = L T r r'=L^Tr r′=LTr作为新的优化误差, 这样就能用 Ceres 求解了。 Mahalanobis 距离其实相当于一个残差加权, 协方差大的加权小, 协方差小的加权大, 着重优化那些比较确定的残差。若写成“sqrt_info.setIdentity()”相当于不加权
协方差矩阵
IMU 协方差 P 为前面推导的 IMU 预积分中迭代出来的 IMU 增量误差的协方差。
视觉测量残差
视觉测量残差即 特征点的重投影误差,视觉残差和雅克比矩阵计算的对应代码在ProjectionFactor::E
函数中。
重投影误差(视觉测量残差)
对于第 i 帧中的特征点, 它投影到第 j 帧相机坐标系下的值为:

拆写成三维形式为:

其中:
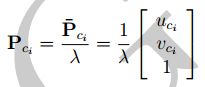
为了后面方便求导Jacobian,对 P c j P_{c_j} Pcj拆解,定义如下变量
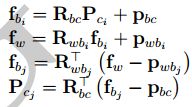
视觉测量残差为
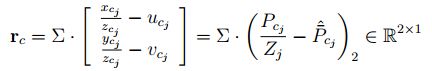
优化变量
雅克比矩阵
根据视觉残差公式,我们可以得到相对于各优化变量的 Jacobian
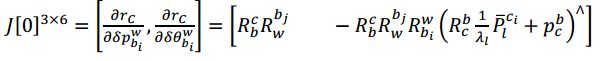

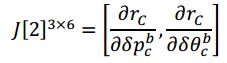
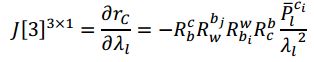
协方差矩阵
视觉约束的噪声协方差与标定相机内参时的重投影误差,也就是偏离几个像素有关, 代
码对应为 ProjectionTdFactor::sqrt_info, 这里取的 1.5 个像素,信息矩阵取根号后为

边缘化和FEJ
舒尔补定义
- 如果矩阵块 D 是可逆的,则 A − B D − 1 C A − BD^{−1}C A−BD−1C称之为D关于M的舒尔补
- 如果矩阵块 A 是可逆的,则 D − C A − 1 B D − CA^{−1}B D−CA−1B称之为A关于 M的舒尔补
将 M 矩阵变成上三角或者下三角形过程中,都会遇到舒尔补:

其中: ∆ A = D − C A − 1 B ∆A=D − CA^{−1}B ∆A=D−CA−1B。联合起来,将 M 变形成对角形:
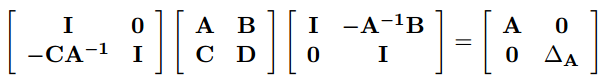
矩阵 M 的逆为:

高斯分布与边缘化
多元高斯分布
高斯分布有两种表达方式:
- 协方差矩阵+均值
- 信息矩阵+信息矢量
协方差矩阵+均值的方式比较常见,如下
左边常数项记为 η η η, p ( x ) p(x) p(x)可以记为:
p ( x ) = η e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } p(x)=η\ exp\left\{ {− \frac{1}2(x−μ)^TΣ ^{−1} (x−μ)}\right\} p(x)=η exp{−21(x−μ)TΣ−1(x−μ)}
其中对称正定矩阵 Σ Σ Σ为随机变量x的协方差矩阵,μ为x的均值,简记为
p ( x ) = N ( μ , Σ ) p(x)=N(μ,Σ) p(x)=N(μ,Σ)
信息矩阵+信息矢量的形式可以由上式推导而来
p ( x ) = η e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } = η e x p { 1 2 x T Σ − 1 x + x T Σ − 1 μ } p(x)=η\ exp\left\{ {− \frac{1}2(x−μ)^TΣ ^{−1} (x−μ)}\right\}\\ =ηexp\left\{ \frac{1}{2}x^TΣ ^{-1}x+x^TΣ ^{-1}μ \right\} p(x)=η exp{−21(x−μ)TΣ−1(x−μ)}=ηexp{21xTΣ−1x+xTΣ−1μ}
现在定义信息矩阵 Ω = Σ − 1 Ω=Σ^{−1} Ω=Σ−1 ,信息矢量 ξ = Σ − 1 μ = Ω μ ξ=Σ^{−1}μ=Ωμ ξ=Σ−1μ=Ωμ
则
p ( x ) = η e x p { − 1 2 x T Ω x + x T ξ } p(x)=η\ exp\left\{{− \frac{1}{2}x^TΩx+x^Tξ}\right\} p(x)=η exp{−21xTΩx+xTξ}
联合高斯分布的分解
设随机变量xa,xbxa,xb满足联合高斯分布 p ( x a , x b ) p(x_a,x_b) p(xa,xb)
由条件概率公式可知
p ( x a , x b ) = p ( x a ) p ( x b ∣ x a ) p(x_a,x_b)=p(x_a)p(x_b∣x_a) p(xa,xb)=p(xa)p(xb∣xa)
联合高斯函数的分解就是根据 p ( x a , x b ) p(x_a,x_b) p(xa,xb)求出上式中的p(xa)p(xa)和p(xb∣xa)p(xb∣xa)。
协方差矩阵+均值
假设多元变量x服从高斯分布,且由两部分组成: x = [ x a x b ] T x = [x_a \ x_b]^T x=[xa xb]T,变量之间构成的协方差矩阵为:
其中 A = c o v ( a , a ) , D = c o v ( b , b ) , C = c o v ( a , b ) A = cov(a, a), D = cov(b, b), C = cov(a, b) A=cov(a,a),D=cov(b,b),C=cov(a,b). 由此变量x的概率分布为:
利用舒尔补对高斯分布进行分解:
其中 ∆ A = D − C A − 1 C T ∆A=D − CA^{−1}C^T ∆A=D−CA−1CT
从多元高斯分布 P(a,b) 中分解得到边际概率 p(a) 和条件概率 p(b|a)
由此可看出,p(a)是协方差矩阵为A的高斯分布,记为

p(b|a)是 ==协方差矩阵为∆A(对应协方差变为 a 对应的舒尔补)==的高斯分布,均值也变了,记为
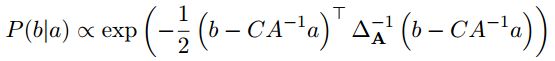
信息矩阵+信息矢量
基于优化的 SLAM 问题中,我们往往直接操作的是信息矩阵,而不是协方差矩阵。所以,有必要知道边际概率,条件概率的信息矩阵是何形式。
协方差矩阵各块和信息矩阵之间有:
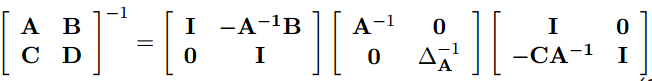
由上式得:
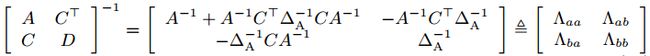
条件概率 P(b|a) 的协方差为 ∆ A = D − C A − 1 C T ∆A=D − CA^{−1}C^T ∆A=D−CA−1CT,可得其信息矩阵为:
![]()
边际概率 P(a)的协方差为A,可得其信息矩阵为:
![]()
总结
边际概率对于协方差矩阵的操作是很容易的,但不好操作信息矩阵。条件概率恰好相反,对于信息矩阵容易操作,不好操作协方差矩阵。表格总结如下
| 概率分布 | 协方差矩阵+均值|信息矩阵+信息矢量 |
| 概率分布 | 协方差矩阵+均值 | 信息矩阵+信息矢量 |
|---|---|---|
| p ( x a ) p(x_a) p(xa) | N ( μ a , Σ a a ) N(μ_a, Σ_{aa}) N(μa,Σaa) | N − 1 ( ) N^{-1}() N−1() |
| p ( x b ∣ x a ) p(x_b∣x_a) p(xb∣xa) | N ( μ b + Σ b a Σ a a − 1 ( x a − μ a ) , Σ b b − Σ b a Σ a a − 1 Σ a b ) N(μ_b+Σ_{ba}Σ^{-1}_{aa}(x_a-μ_a),Σ_{bb}−Σ_{ba}Σ_{aa}^{−1}Σ_{ab}) N(μb+ΣbaΣaa−1(xa−μa),Σbb−ΣbaΣaa−1Σab) |
VINS-Mono关键知识点总结——边缘化marginalization理论和代码详解
VINS-Mono关键知识点总结——预积分和后端优化IMU部分
左边常数项记为 η η η, p ( x ) p(x) p(x)可以记为:
p ( x ) = η e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } p(x)=η\ exp\left\{ {− \frac{1}2(x−μ)^TΣ ^{−1} (x−μ)}\right\} p(x)=η exp{−21(x−μ)TΣ−1(x−μ)}
其中对称正定矩阵 Σ Σ Σ为随机变量x的协方差矩阵,μ为x的均值,简记为
p ( x ) = N ( μ , Σ ) p(x)=N(μ,Σ) p(x)=N(μ,Σ)
信息矩阵+信息矢量的形式可以由上式推导而来
p ( x ) = η e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } = η e x p { 1 2 x T Σ − 1 x + x T Σ − 1 μ } p(x)=η\ exp\left\{ {− \frac{1}2(x−μ)^TΣ ^{−1} (x−μ)}\right\}\\ =η\ exp\left\{ \frac{1}{2}x^TΣ ^{-1}x+x^TΣ ^{-1}μ \right\} p(x)=η exp{−21(x−μ)TΣ−1(x−μ)}=η exp{21xTΣ−1x+xTΣ−1μ}
现在定义信息矩阵 Ω = Σ − 1 Ω=Σ^{−1} Ω=Σ−1 ,信息矢量 ξ = Σ − 1 μ = Ω μ ξ=Σ^{−1}μ=Ωμ ξ=Σ−1μ=Ωμ,则
p ( x ) = η e x p { − 1 2 x T Ω x + x T ξ } p(x)=η\ exp\left\{{− \frac{1}{2}x^TΩx+x^Tξ}\right\} p(x)=η exp{−21xTΩx+xTξ}