LIS最长上升子序列详解+模板(dp和二分做法)

LIS

最长上升子序列（longest  increasing subsequence），也可以叫最长非降序子序列，简称LIS

求LIS的长度的问题  是指求数列的最长上升子序列（可以不连续）的长度

dp做法  复杂度O()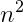

我们用 dp[ i ]来代表以 a[ i ] 为结尾的前 i 个数最长递增子序列的长度  

我们来看一下这个栗子      2  7  1  5  6  4  3  8  9  7  11  13  6  这个序列

首先   我们把所有位置的dp值初始化为1   （因为最小也是一 它本身就是一个递增长度为1 的序列）

我们拿a[ 7 ]这个位置举例  是8   我们找他前边所有小于8的数  有 2 7 1 5 6 4 3

然后从这些数的dp值中 找到最大的   是dp[ 4 ] = 3 (序列 2 5 6)   dp[7]就等于这个最大的+1

方法就是   dp[ i ] 就等于 a[ i ]  前面比 a[ i  ]小的所有的数 的dp值中 最大的那个  再+1

 状态转移方程    dp[ i ] =  max{   dp[   {  a[ i ] 前面的数  } < a[ i ]    ]    }  + 1

代码如下

#include
#include
#include
#include
using namespace std;
#define maxn 1010
int a[maxn],dp[maxn];
int n,ans=1;
int main(){
    while(~scanf("%d",&n)){
    	ans=0;
        for(int i=0;i>a[i],dp[i]=1;
        for(int i=1;i

 

模拟+二分    复杂度〇(nlogn)

dp的做法复杂度是O(n^2)   显然这不够优秀

比如这道题就会超时    51nod1134 

所以 我们用另一种求最长上升子序列的办法  复杂度是O(nlog（n）)

他的做法是怎么样的呢  举个栗子

A数组   { 4 ，2 ，5 ，8 ，3 ，4 ，6 }

我们用一个B数组来存一个递增的序列  len时刻记录B数组长度

我们的原则是维护B数组的递增有序  在保持len尽量增大的前提下 使B中的值尽量的小

1. A[0]=4 我们把A[1] 放入B[1]     同时 len=1
2. A[1]=2  此时B数组中只有一个4   len=1   我们用2替换掉4  len依旧是2  B中的值也变小了
3. A[2]=5  B中就一个2 len=1  我们把5加进去   B={2,5}   len=2
4. A[3]=8  8大于B数组中所有数  我们能使len增大就先让len增大  加进去    B={2,5,8}   len=3
5. A[4]=3  我们在B中找到刚好大于3的数 是5  那么用3替换5 值变小 且len不变  B={2,3,8} 
6. A[5]=4  仍然在B中找刚好大于4的数 是8  那么用4替换8 值变小 且len不变  B={2,3,4}
7. A[6]=6  比B中都大  加进去 B={2,3,4,6}  len=4

最终的答案是 len=4  也就是最长上升子序列长度为4  

这个方法可以得到正确的a序列的LIS长度

但是最终在B数组中存的那个序列  并不是正确的LIS序列

比如 我们用这个方法找    A{ 4 ，2 ，5 ，8，3 } 的LIS长度时

那么用上边讲的前五个步骤就可以得到 len=3 但是B={2，3，8} 显然这并不是一个正确的序列

如果不明白为什么的话  再回去看看我们维护B数组时的原则 多看几遍 理解一下

这个原则能保证我们得到的B数组的len是正确的  并不能保证序列是正确的序列

由于B数组中的数列呢 一直是有序的  所以我们可以使用二分查找来维护B数组

从而使这个算法的复杂度降低到了 n*log(n)

下面给出我的写法

题目链接传送门51nod1134

两个写法

手打二分查找

代码

注意 这里和普通的二分有一点区别就是  普通二分是查找val  这里是查找大于等于val的值

#include
#include
#include
#include
using namespace std;
const int maxn = 1e6 + 7;
int f[maxn], a[maxn];
int n;
//二分查找 查找小于等于x的数的位置
//如果找不到  返回r
int find(int l, int r, int x) {
	while (l < r) {
		int mid = (l + r) / 2;
		if (f[mid] < x) l = mid + 1;
		else r = mid;
	}
	return l;
}
int lis() {
	int len = 0;
	for (int i = 0; i < n; i++) {
		int k=find(0,len,a[i]);
		f[k] = a[i];
		if (k == len) len++;
	}
	return len;
}
int main() {
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d", &a [i]);
	}
	printf("%d\n", lis());
	return 0;
}

 

STL     lower_bound()

 这个库函数会在 [ l，r）中二分查找 返回刚好大于等于val的值的地址  若没有  则返回 r 的地址

返回的都是地址  所以需要减去 首地址 才得到位置

代码

#include
#include
#include
#include
using namespace std;
const int maxn=1e6+7;
int b[maxn],a[maxn];
int n;
int LIS(){
	int len=0;
	for(int i=0;i

 

变式  最大下降矩阵

河南CCPC省赛A题

题目描述

我们称一个矩阵是下降矩阵，当且仅当，矩阵的每一列都是严格下降的。很显然，这个要求很苛刻，大多数矩阵都无法满足。但是显然如果消去一些行，一定可以使得这个矩阵变成下降矩阵。

现在给出一个n行m列的矩阵，请你求出最少消去多少行，可以使得这个矩阵变为下降矩阵。

输入

输入第一行包含两个正整数n,m分别表示矩阵的行数和列数。(1<=n,m<=300)
接下来n行，每行有m个数,中间用空格隔开，每个数都小于2^31.

输出

输出仅包含一个整数，即最少消去的行数。

样例输入 Copy

1 3
1 2 3 

样例输出 Copy

0

套用第一个n^2的求最长上升子序列的长度算法

只是那个是比较两个数的大小

改成比较两行的大小（一行数全部小于另一行对应的数，这行就小于另一行）

#include
#include
#include
using namespace std;
const int maxn=307;
int n,m;
int a[maxn][maxn];
int dp[maxn];
int cmp(int x,int y){
	for(int i=0;ia[y][i]){
			return 0;
		}
	}
	return 1;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;i