HDU 6363 bookshelf

Here

仅作笔记和理解

在学长的威逼利诱下写了此题

题意

给你$n$本书，$k$个书架，你要将这些书放到书架上

设$c_1,c_2,c_3,c_4\cdot \cdot \cdot c_k$是每个书架上的书的数量，$f[n]$代表斐波那契数列的第$n$项，让你求$gcd(2^{f[c_1]}-1,2^{f[c_2]}-1,2^{f[c_3]}-1\cdot \cdot \cdot 2^{f[c_n]}-1)$的期望

数据范围$0<n,k\le 10^6$

解

首先有两个定理
$gcd(x^a-1,x^b-1)=x^{gcd(a,b)}-1$
$gcd(f[a],f[b])=f[gcd(a,b)]$

所以就变成了求$2^{f[gcd(c_1,c_2,c_3,c_4\cdot \cdot \cdot c_k)]}-1$的期望。
那么接下来就是枚举$gcd$的值列出式子然后化简了

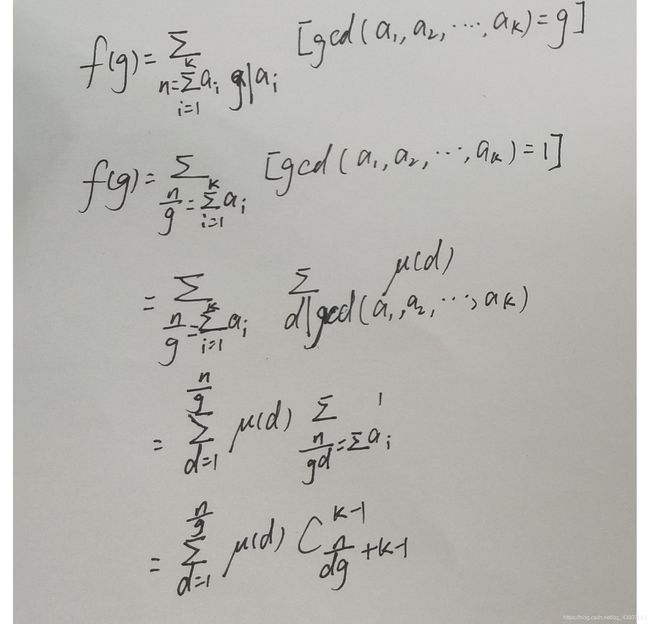
由于书架上可以不放书，所以在书堆的数量之上$+k-1$，这样使用隔板法的时候，选中的$k-1$个位置可以被替换成挡板，这样就可以使得书架上的书数量可以为0了。
还有就是由于斐波那契数列的值会非常大，所以还需要用到欧拉降幂，$\%(mo-1)$。

Code

/****************************
* Author : 水娃             *
* Date : 2020-08-06-17.07.23*
****************************/
#pragma GCC optimize(3,"Ofast","inline")
#include
using namespace std;
#define mst(a,b) memset(a,b,sizeof(a))
#define ll long long
#define debug(a) cout<<#a<<" is "<
#define ull unsigned long long
#define fi first
#define se second
typedef pair<int,int>pii;
typedef pair<ll,int>pli;
typedef pair<int,ll>pil;
typedef pair<ll,ll>pll;
const ll mo=(ll)1e9+7;
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}

const int MAXN=2e6+100;

ll fpow(ll base,ll exp)
{
    ll ans=1;
    while(exp)
    {
        if(exp&1)
        {
            ans=ans*base%mo;
        }
        base=base*base%mo;
        exp>>=1;
    }
    return ans;
}

int now;
int mu[MAXN];
int pri[MAXN];
bool vis[MAXN];
void pre()
{
    now=0;
    mu[1]=1;
    for(int i=2;i<MAXN;i++)
    {
        if(!vis[i])
        {
            pri[++now]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=now&&i*pri[j]<MAXN;j++)
        {
            vis[i*pri[j]]=1;
            if(i%pri[j])
            {
                mu[i*pri[j]]=-mu[i];
            }
            else
            {
                mu[i*pri[j]]=0;
                break;
            }
        }
    }
}

ll fac[MAXN],inv_fac[MAXN];
void init()
{
    fac[0]=1;
    for(int i=1;i<MAXN;i++)
    {
        fac[i]=fac[i-1]*i%mo;
    }
    inv_fac[MAXN-1]=fpow(fac[MAXN-1],mo-2);
    for(int i=MAXN-2;i>=0;i--)
    {
        inv_fac[i]=inv_fac[i+1]*(i+1)%mo;
    }
}
ll C(ll m, ll n)///组合
{
    return fac[m]*inv_fac[m-n]%mo*inv_fac[n]%mo;
}
ll A(ll m, ll n)///排列
{
    return fac[m]*inv_fac[m-n]%mo;
}

ll f[MAXN];
void getf()
{
    f[1]=f[2]=1;
    for(int i=3;i<MAXN;i++)
    {
        f[i]=(f[i-1]+f[i-2])%(mo-1);
    }
}

void work()
{
    ll n,k;
    cin>>n>>k;
    ll ans=0,cnt;
    for(ll i=1;i<=n;i++)
    {
        if(n%i)continue;
        cnt=0;
        int top=n/i;
        for(ll j=1;j<=top;j++)
        {
            if(n%(j*i))continue;
            cnt=(cnt+mu[j]*C(n/(j*i)+k-1,k-1)%mo+mo)%mo;
        }
        ans=(ans+(fpow(2,f[i])-1+mo)%mo*cnt%mo)%mo;
    }
    ans=ans*fpow(C(n+k-1,k-1),mo-2)%mo;
    cout<<ans<<"\n";
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    pre();
    init();
    getf();
    int T;cin>>T;while(T--)
        work();
    return 0;
}