数模系列一 导言和线性规划问题
注1:
本系列博客是《数学建模算法与应用》的阅读笔记,适合入门阅读,快速上手数学建模竞赛。
注2:
对于数学建模,我们需要知道在分析一个具体的建模问题时,需要用到那些方法;反过来讲,当我们了解到
了数学建模的常用方法之后,拿到题目也就有了大致的思路。
所以,我根据《数学建模算法与应用》,针对每一个数学建模的方法(如图论、微分方程、数理统计等),
回答下面几个问题:一、这个方法是什么;二、这个方法可以解决什么问题;三、如何使用这个方法分析解
决具体问题,并给出实例;四、matlab中的具体模板方法
注3:
作者也是建模萌新〒▽〒,疏漏之处在所难免,有什么问题请私信/留言交流
文章目录
- 投资的收益和风险
什么是线性规划
线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
在解决实际问题时,把问题归结成一个线性规划数学模型是很重要的一步,但往往也是困难的一步,模型建立得是否恰当,直接影响到求解。而选适当的决策变量,是我们建立有效模型的关键之一。
可以用来解决什么问题
线性规划方法主要可以解决以下几方面的问题:
(1)生产计划和组织问题;
(2)运输与布局问题;
(3)配料和下料问题。
如何使用线性规划来分析解决具体问题
给建模新人
在分析具体问题之前,你需要知道,在数学建模中,我们是怎样完成一篇比赛论文的呢?
一个比较完整的数学建模论文往往有如下几个部分组成:
1.summary——对解决的问题、建模过程和方法进行总结
2.Key Words——给出这篇文章的关键词(问题和数学方法)
2.5 目录
3.Restatement of problems——问题重述(不是对题目复制粘贴!而是简明扼要地总述问题和说明研究问题的意义)
4.Assumptions and Notations——符号规定和基本假设
5.模型的分析与建立(包括The Solution of question(问题分析)、Simplifying(模型简化)、Calculate(模型求解))
6.结果分析
7.Validating the Model——有效性验证、优缺点分析
8.Conclusions——结论
9.Appendix——附录(代码等)(没有人看你的代码!所以建模的思路、数据、语言才是最重要的!文章格式(latex用的好不好)也很重要!)
所以,我们选好题目之后,会进行问题分析,把题目中的数据转换成数学语言,并且用一系列的数学方法分析它。并且,在这个过程中,我们会对问题在合理的前提下进行简化和假设。
当模型建立完成、数据结果出来之后,剩下的部分是不是就水到渠成了?
可能你看到这里还是十分茫然——核心问题还是没有解决呀?如何“把题目中的数据转换成数学语言,并且用一系列的数学方法分析它”呢?
这就是我这一系列的博客要写的东西了。如果你是我博客的读者,那么你就是要从我的博客之中,从一个又一个的题目案例之中,不断学习数学分析的方法,培养数学的和建模的思维。掌握了这些基本方法,才能面对建模题目游刃有余。
与此同时,数学和建模思维的培养,意义远远超过了比赛本身。这是后话,在此不表。
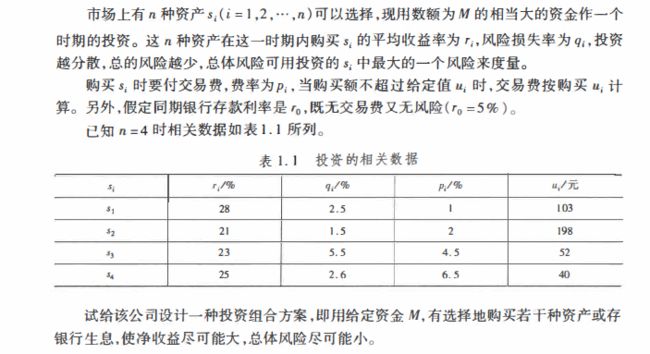
投资的收益和风险
这就是一个简单的数学建模题目了,我们用高中的线性规划的知识就足以解决它。
但是注意!在这个题目中已经给出了“度量风险”的数学公式,一般我们则需要找出这个公式并且说明它的
合理性。
另一个值得注意的问题是:大多数建模问题并非像高考中的数学问题一样,只有一个解,所以我们要针对
不同的场景对模型进行假设和简化,也就是所谓的“多目标规划模型”;与高考数学相同的是,同一个问题
我们可以用不同的方法进行分析!这也就是考验我们创新能力的时候了。

这幅图片给出了符号规定和基本假设。
对于一个严谨的数学分析来说,界定系统边界是非常重要的,因此我们要尽可能全面地限制问题边界,这
也避免了建模过程中的一些边界错误和方向错误。
符号在用到地时候规定就可以了。
要注意的是符号规范问题,队伍中要有一位能够准确快速使用latex输出数学公式和符号的队员。


这就是一个简单的数学模型建立的过程。毋庸置疑,线性规划问题需要找出约束条件和结果的表达式。我
们在高中已经训练过这方面的能力。
同时,我们认识到这是个多目标规划模型以后,就要学会衡量问题规模进行模型简化。
在这个问题中根据两个指标:净收益和风险水平,进行合理简化即可。
需要注意的是,在模型一中,风险水平是一个变量。

步长:程序语言中的名词,让一个数值在每次运算中加上某个数(此即步长)重复执行此项运算。
数据处理队员需要掌握线性规划的matlab求解方法,线性规划问题虽然简单,但是数据并非整数的时候,
就需要用到计算机进行处理。
负责数学的队员最好掌握matlab的线性规划标准
我把线性规划标准和题目的matlab代码放在了文章最后面。
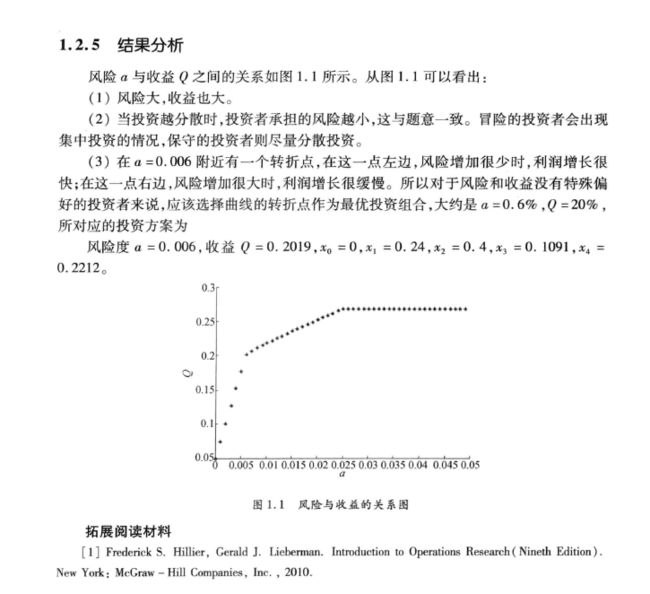
结果分析
这是个非常有趣也非常合理的结果,它符合经济学中的边际效益递减规律。
matlab中的具体模板方法

%求解线性规划问题
f=[-2;-3;5];
a=[-2,5,-1;1,3,1];
b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x,y=-y
%输出x和y
%[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
%这里fval 返回目标函数的值,LB 和UB 分别是变量x 的下界和上界, 0 x 是x 的初始值,
%OPTIONS 是控制参数。
%如果没有等式约束,对应矩阵为空矩阵
%在这里,zeros(3,1)是下界条件,没有上界条件
题目代码
clc,clear
a=0;
hold on
while a<0.05
c=[-0.05,-0.27,-0.19,-0.185,-0.185];
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
b=a*ones(4,1);
Aeq=[1,1.01,1.02,1.045,1.065];
beq=1;
LB=zeros(5,1);
[X,Q]=linprog(c,A,b,Aeq,beq,LB);
Q=-Q;
plot(a,Q,'*k')
a=a+0.001;
end
xlable('a'),ylable('Q')