梯度向量与梯度下降法

    最近非常热门的“深度学习”领域，用到了一种名为“梯度下降法”的算法。梯度下降法是机器学习中常用的一种方法，它主要用于快速找到“最小误差”（the minimum error）。要掌握“梯度下降法”，就需要先搞清楚什么是“梯度”，本文将从这些基本概念：方向导数（directional derivative）与偏导数、梯度（gradient）、梯度向量（gradient vector）等出发，带您领略“深度学习”中的“最小二乘法”、“梯度下降法”和“线性回归”。

• 偏导数（Partial derivate）
• 方向导数（Directional derivate）
• 梯度（Gradient）
• 线性回归（linear regression）
• 梯度下降（Gradient descent）

一、方向导数

1，偏导数
  先回顾一下一元导数和偏导数，一元导数表征的是：一元函数 f(x) f ( x ) 与自变量 x x 在某点附近变化的比率（变化率），如下：

f′(x0)=df(x)dx∣x=x0=limΔx→0f(x0+Δx)−f(x0)Δx f ′ ( x 0 ) = d f ( x ) d x ∣ x = x 0 = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x

  而二元函数的偏导数表征的是：函数 F(x,y) F ( x , y ) 与自变量 x x （或 y y ） 在某点附近变化的比率（变化率），如下：

Fx(x0,y0)=∂F∂x∣x=x0,y=y0=limΔx→0F(x0+Δx,y0)−F(x0,y0)Δx F x ( x 0 , y 0 ) = ∂ F ∂ x ∣ x = x 0 , y = y 0 = lim Δ x → 0 F ( x 0 + Δ x , y 0 ) − F ( x 0 , y 0 ) Δ x

  以长方形的面积 z=F(x,y) z = F ( x , y ) 为例，如下图：

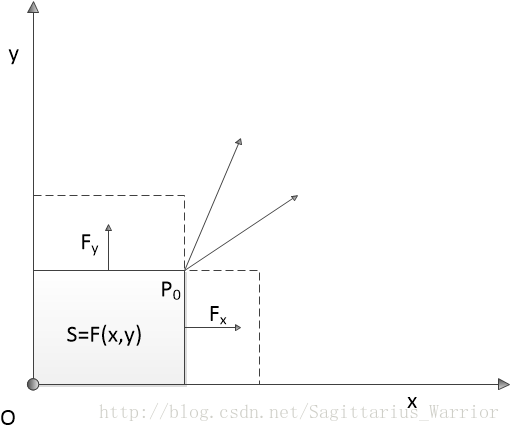
如果说 z=F(x,y)=x⋅y z = F ( x , y ) = x ⋅ y 表示以 P(x,y) 点和原点为对角点的矩形的面积，那么 z=F(x,y) z = F ( x , y ) 在 P0 P 0 点对x 的偏导数表示 P0 P 0 点沿平行于 x 轴正向移动，矩形的面积变化量与 P0 P 0 点在 x方向的移动距离的比值

Fx(x0,y0)=∂F∂x=limΔx→0ΔSΔx F x ( x 0 , y 0 ) = ∂ F ∂ x = lim Δ x → 0 Δ S Δ x

同样地，可得

Fy(x0,y0)=∂F∂y=limΔy→0ΔSΔy F y ( x 0 , y 0 ) = ∂ F ∂ y = lim Δ y → 0 Δ S Δ y

需要注意的是：
  矩形面积的这个例子有时候也很容易让人混淆，上图中无论 x 还是 y ，都是输入变量，输出变量 S 并没有用坐标轴的形式画出来。也就是说，这个例子实际上是一个三维空间的函数关系，而不是二维平面的函数关系。
  
向量角度看偏导数：
  偏导数向量 [FxFy] [ F x F y ] 是坐标向量（原向量） [xy] [ x y ] 的线性变换，详见《Essence of linear algebra》：求导是一种线性变换。
扩展一下：如果 P0 P 0 点不是沿平行于 x 轴方向或平行于 y 轴方向，而是 沿与 x 轴成夹角 α α 的一条直线 l l 上移动，那么面积的增量与 P0 P 0 点在该直线上移动的距离的比值关系是什么呢？
假设 P0 P 0 点在这条直线上移动的距离为 Δt Δ t ，则有

{Δx=Δt⋅cosαΔy=Δt⋅sinα { Δ x = Δ t ⋅ c o s α Δ y = Δ t ⋅ s i n α

那么，矩形面积增量与移动距离的增量比值是：

limΔt→0ΔSΔt=limΔt→0(x0+Δt⋅cosα)⋅(y0+Δt⋅sinα)−x0⋅y0Δt=limΔt→0y0Δt⋅cosα+x0Δt⋅sinα+(Δt)2⋅cosα⋅sinαΔt=y0cosα+x0sinα lim Δ t → 0 Δ S Δ t = lim Δ t → 0 ( x 0 + Δ t ⋅ c o s α ) ⋅ ( y 0 + Δ t ⋅ s i n α ) − x 0 ⋅ y 0 Δ t = lim Δ t → 0 y 0 Δ t ⋅ c o s α + x 0 Δ t ⋅ s i n α + ( Δ t ) 2 ⋅ c o s α ⋅ s i n α Δ t = y 0 c o s α + x 0 s i n α

与偏导数类似，上式也是一个“一元导数”。事实上，这就是方向导数，可记作

Fl=∂F∂l F l = ∂ F ∂ l

2，矢量描述
  从矢量角度来看， P0 P 0 点沿与 x 轴成夹角 α α 的一条直线 l l 移动，这个移动方向可以看作是一个矢量 —— “方向矢量”

l⃗ =(cosα,sinα) l → = ( c o s α , s i n α )

  如果 α=0 α = 0 ，即沿平行 x 轴方向移动；如果 α=π2 α = π 2 ，即沿平行 y 轴方向移动。因此，偏导数实际上是方向导数的一种特例。
  在回顾一下上一节“二元全微分的几何意义”：用切平面近似空间曲面。这个切平面实际上是由两条相交直线确定的平面，而这两条直线分别是 x 方向的偏导数向量 Px→ P x → 和 y 方向的偏导数向量 Py→ P y → 。很显然，这两个向量不但位于同一个平面，而且相互垂直。那么这两个向量合成的新向量也一定位于这个“切平面”。
注：关于偏导数向量相互垂直，可以很容易从偏导数“切片法”推导出来。
  将偏导数合成向量记作 P⃗ =(Fx,Fy)=(∂F∂x,∂F∂y) P → = ( F x , F y ) = ( ∂ F ∂ x , ∂ F ∂ y ) 。如果对偏导数向量和方向向量进行矢量“内积”，则有：

P⃗ ⋅l⃗ =∂F∂xcosα+∂F∂ysinα=∂F∂l P → ⋅ l → = ∂ F ∂ x c o s α + ∂ F ∂ y s i n α = ∂ F ∂ l

  这个内积在数值上刚好等于 l⃗  l → 方向的方向导数。
换句话说：方向导数就是偏导数合成向量与方向向量的内积。
  
从向量角度看：
  内积在几何上表示投影，也就是说，方向导数（向量）是原向量在某个方向上的投影的变化率。


3，多元方向导数
  从上面的矢量内积出发，将 l⃗  l → 与 y 轴方向的夹角表示为 β β ，则方向导数的公式可以变化为：

∂F∂l=∂F∂xcosα+∂F∂ycosβ ∂ F ∂ l = ∂ F ∂ x c o s α + ∂ F ∂ y c o s β

  类似地，推广到多维空间

∂F∂l=∂F∂xcosα1+∂F∂ycosα2+∂F∂zcosα3+⋅⋅⋅ ∂ F ∂ l = ∂ F ∂ x c o s α 1 + ∂ F ∂ y c o s α 2 + ∂ F ∂ z c o s α 3 + ⋅ ⋅ ⋅

  当然，从向量内积的角度更容易得到这个公式

P⃗ ⋅l⃗ =(∂F∂x,∂F∂,∂F∂z,⋅⋅⋅)⋅(cosα1,cosα2,cosα3,⋅⋅⋅) P → ⋅ l → = ( ∂ F ∂ x , ∂ F ∂ , ∂ F ∂ z , ⋅ ⋅ ⋅ ) ⋅ ( c o s α 1 , c o s α 2 , c o s α 3 , ⋅ ⋅ ⋅ )

二、梯度

1，梯度（gradient）
  还是从上面的矩形面积这个例子出发，来探索什么是“梯度”。
  假设 P0 P 0 点的坐标是 (3–√,1) ( 3 , 1 ) ， 则

Fx=1,Fy=3–√,Fl=cosα+3–√sinα F x = 1 , F y = 3 , F l = c o s α + 3 s i n α

  很明显，方向导数（标量）的大小随 矢量 l⃗  l → 的方向不同而不同。那么，这些方向导数中是否存在一个最大值呢？
  答案是肯定的！这就是“梯度”（标量）。

∇F=gradF=max{∂F∂l} ∇ F = g r a d F = m a x { ∂ F ∂ l }

  所以，梯度的第一层含义就是“方向导数的最大值”。


2，梯度矢量
  梯度的第一层含义是“方向导数的最大值”，那么这个最大值是多少呢？或者说 矢量 l⃗  l → 取什么值时才能找到这个最大值？
  还是以矩形面积为例

gradF(3–√,1)=max{∂F∂l}=max{cosα+3–√sinα}=max{2sin(π6+α)} g r a d F ( 3 , 1 ) = m a x { ∂ F ∂ l } = m a x { c o s α + 3 s i n α } = m a x { 2 s i n ( π 6 + α ) }

  显然， α=π3 α = π 3 时，取值最大，此时

l⃗ =(cosα,sinα)=(12,3–√2) l → = ( c o s α , s i n α ) = ( 1 2 , 3 2 )

  在比较一下偏导数向量

P⃗ =(Fx,Fy)=(1,3–√) P → = ( F x , F y ) = ( 1 , 3 )

  是不是似曾相识？对的，后者单位化后就变成了前者。
  从向量内积的角度来看，更容易理解：

∇F=gradF=max{∂F∂l}=max{P⃗ ⋅l⃗ }=max{∣∣P⃗ ∣∣⋅∣∣l⃗ ∣∣⋅cosθ} ∇ F = g r a d F = m a x { ∂ F ∂ l } = m a x { P → ⋅ l → } = m a x { | P → | ⋅ | l → | ⋅ c o s θ }

  很明显， 两个向量的夹角 θ=0 θ = 0 时，取得最大值。
  至此，我们引出了梯度的第二层含义，或者说叫“梯度矢量”

∇F⃗ =gradF=(∂F∂x,∂F∂y) ∇ F → = g r a d F = ( ∂ F ∂ x , ∂ F ∂ y )

注意：
  上面提到的夹角 θ θ 在几何上表示原向量（坐标向量）与导数向量（变化率向量）之间的夹角，所以，梯度的几何含义就是：沿向量所在直线的方向变化率最大。
  
顺便扩展一下散度（divergence）和旋度（curl）的记号，它们都使用了Nabla算子（微分向量算子），分别如下：

∇⋅F⃗ ,∇×F⃗  ∇ ⋅ F → , ∇ × F →

3，举例
  总结一下这一节的思路： 偏导数向量合成 → → 合成向量与方向向量内积 → → 方向导数 → → 方向导数的最值 → → 梯度 → → 梯度向量与偏导数合成向量相同
  转了一圈，又回来了。
  从偏导数合成向量到梯度矢量，让我想起了高中物理中的“力的合成与分解”和“沿合力方向做功最有效率”这些物理知识，恰好能与这些数学概念对应上。

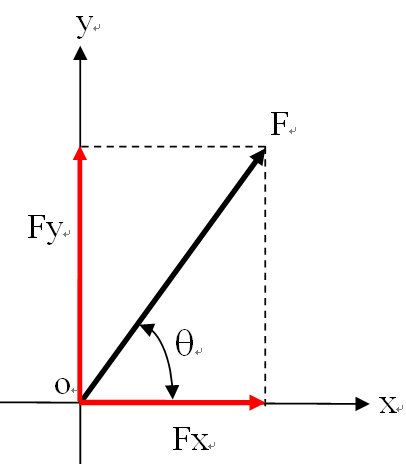
  如上图，合力表示偏导数合成向量，“垂直分力”表示x方向和y方向的偏导数向量，那么方向向量则对应“做功”路径，而“沿合力方向做功”则表示方向向量与偏导数合成向量重合。Perfect !
注：在重力场或电场中，做功的结果是改变势能，因此，“做功最有效率”又可以表述为“势能变化率最快”。
注：关于梯度（gradient）可以参考以下文章：
https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/grad/grad.html
https://betterexplained.com/articles/vector-calculus-understanding-the-gradient/

三、梯度下降法

1，梯度下降法
  梯度下降法（gradient descent）是一个一阶最优化算法，它的核心思想是：要想最快找到一个函数的局部极小值，必须沿函数当前点对应“梯度”（或者近似梯度）的反方向（下降）进行规定步长“迭代”搜索。如下图：

  看到上面这幅图，你能想到什么？
  我想到了两个概念：一是地理学中的“梯田”和“等高线”，下面的链接中，有一篇文章的作者将“梯度下降”形象的比作“从山顶找路下到山谷”，这么看来，等高线肯定与梯度下降有某种关联。
  第二个想到的是电学中的“带电物体的等势面”或者说是“电场等势线”。看一下wiki - potential gradient，可以扩展一下“势能梯度”的知识。
  很明显，梯度常常和势能联系在一起，那么势能是什么呢？它就是上图中的弧线圈。这个解释有点虚，给个更贴切的：我们可以把势能看作是 z=f(x,y) z = f ( x , y ) 中的这个 z z ，即函数值。这些弧线圈就表示在它上面的点 (x,y) ( x , y ) 对应的 z=f(x,y) z = f ( x , y ) 的值相等。从空间几何的角度来看这些“弧线圈”，更容易理解： z=f(x,y) z = f ( x , y ) 表示空间曲面，用 z=c z = c 这样一个平面去截空间曲面，它们的交线就是“弧线圈”，公式表示为

{z=f(x,y)z=c { z = f ( x , y ) z = c

  当然啦，上图是把多个弧线圈画到（投影）了一个平面上。
  我们也可以这样来理解“梯度下降法”： 导数表征的是“函数值随自变量的变化率” → → 梯度是各方向导数中的最大值 → → 沿 “梯度矢量”移动必定变化最快 → → 沿“梯度矢量” 反方向下降（减少）最快。

google MLCC - Gradient descent

2，梯度下降法求极值
  求下列函数的极小值

f(x)=x4−3∗x3+2⇒f′(x)=4x3−9x2 f ( x ) = x 4 − 3 ∗ x 3 + 2 ⇒ f ′ ( x ) = 4 x 3 − 9 x 2

# From calculation, it is expected that the local minimum occurs at x=9/4

cur_x = 6 # The algorithm starts at x=6
gamma = 0.01 # step size multiplier
precision = 0.00001
previous_step_size = cur_x

def df(x):
    return 4 * x**3 - 9 * x**2

while previous_step_size > precision:
    prev_x = cur_x
    cur_x += -gamma * df(prev_x)
    previous_step_size = abs(cur_x - prev_x)

print("The local minimum occurs at %f" % cur_x)

The local minimum occurs at 2.249965

注：关于“gradient descent”还可以参考以下资料：
https://www.analyticsvidhya.com/blog/2017/03/introduction-to-gradient-descent-algorithm-along-its-variants/
http://ruder.io/optimizing-gradient-descent/


3，梯度下降法与最小二乘法
  “机器学习”中有六个经典算法，其中就包括“最小二乘法”和“梯度下降法”，前者用于“搜索最小误差”，后者用于“用最快的速度搜索”，二者常常配合使用。代码演示如下：

# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, coordinates):
    totalerror = 0
    for i in range(0, len(coordinates)):
        x = coordinates[i][0]
        y = coordinates[i][1]
        totalerror += (y - (m * x + b)) ** 2
    return totalerror / float(len(coordinates))

# example
compute_error_for_line_given_points(1, 2, [[3, 6], [6, 9], [12, 18]])

22.0

  以上就是用“最小二乘法”来计算误差，当输入为 (1,2) ( 1 , 2 ) 时，输出为 22.0 22.0

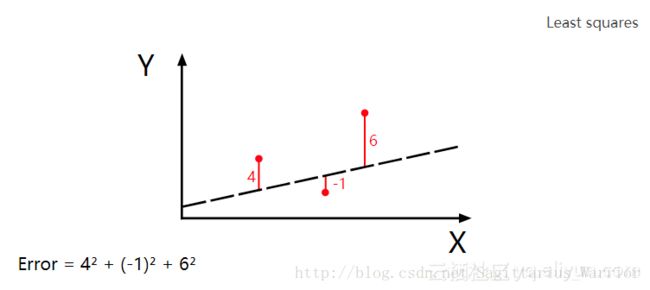
  很显然，最小二乘法需要不停地调整（试验）输入来找到一个最小误差。而应用“梯度下降法”，可以加快这个“试验”的过程。
  以上面这段程序为例，误差是斜率 m 和常数 b 的二元函数，可以表示为

e=g(m,b) e = g ( m , b )

  那么，对最小二乘法的参数调优就转变为了求这个二元函数的极值问题，也就是说可以应用“梯度下降法”了。
  “梯度下降法”可以用于搜索函数的局部极值，如下，求下列函数的局部极小值

f(x)=x5−2x3−2 f ( x ) = x 5 − 2 x 3 − 2

  分析：这是一个一元连续函数，且可导，其导函数是：

f′(x)=5x4−6x2 f ′ ( x ) = 5 x 4 − 6 x 2

  根据“一阶导数极值判别法”：若函数f(x)可导，且f’(x)在 x0 x 0 的两侧异号，则 x0 x 0 是f(x)的极值点。那么，怎么找到这个 x0 x 0 呢？
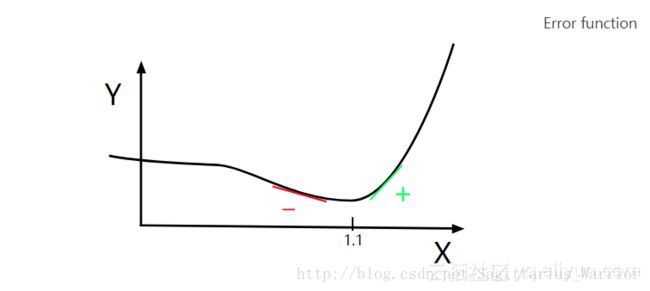
  很简单，只需要沿斜率（导数值）的反方向逐步移动即可，如下图：导数为负时，沿x轴正向移动；导数为正时，沿x轴负方向移动。

current_x = 0.5 # the algorithm starts at x=0.5
learning_rate = 0.01 # step size multiplier
num_iterations = 60 # the number of times to train the function

# the derivative of the error function (x ** 4 = the power of 4 or x^4)
def slope_at_given_x_value(x):
    return 5 * x ** 4 - 6 * x ** 2

# Move X to the right or left depending on the slope of the error function
x = [current_x]
for i in range(num_iterations):
    previous_x = current_x
    current_x += -learning_rate * slope_at_given_x_value(previous_x)
    x.append(current_x)   #print(previous_x)

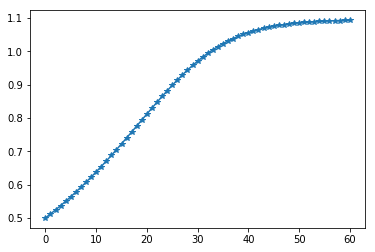
print("The local minimum occurs at %f, it is %f" % (current_x, current_x ** 5 - 2 * current_x ** 3 - 2))

The local minimum occurs at 1.092837, it is -3.051583

import numpy as np
import matplotlib.pyplot as plt
plt.plot(x, marker='*')
plt.show()

  沿梯度（斜率）的反方向移动，这就是“梯度下降法”。如上图所示，不管初始化值设为什么，在迭代过程只会越来越接近目标值，而不会偏离目标值，这就是梯度下降法的魅力。
  上面这张图是表示的是一个一元函数搜索极值的问题，未必能很好展示梯度下降法的魅力，你再返回去看上面那张“势能梯度图”，那是一个二元函数搜索极值的过程。左边的搜索路径很简洁，而右边的搜索路径，尽管因为初始值的设定，导致它的路径很曲折，但是，你有没有发现，它的每一次迭代事实上离目标都更近一步。我想，这就是梯度下降法的优点吧！
注：这段代码是一元函数求极值，如果是二元函数，则需要同时满足两个分量的偏导数的值为零，下面的线性回归程序算的就是二元偏导数。
  通过组合最小二乘法和梯度下降法，你可以得到线性回归，如下：

# Price of wheat/kg and the average price of bread
wheat_and_bread = [[0.5,5],[0.6,5.5],[0.8,6],[1.1,6.8],[1.4,7]]

def step_gradient(b_current, m_current, points, learningRate):
    b_gradient = 0
    m_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i][0]
        y = points[i][1]
        b_gradient += -(2/N) * (y -((m_current * x) + b_current))
        m_gradient += -(2/N) * x * (y -((m_current * x) + b_current))
    new_b = b_current -(learningRate * b_gradient)
    new_m = m_current -(learningRate * m_gradient)
    return [new_b, new_m]

def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
    b = starting_b
    m = starting_m
    for i in range(num_iterations):
        b, m = step_gradient(b, m, points, learning_rate)
    return [b, m]

gradient_descent_runner(wheat_and_bread, 1, 1, 0.01, 1000)

[3.853945094921183, 2.4895803107016445]

  上面这个程序的核心思想就是：在内层迭代的过程中，算出每一步误差函数相当于 m 和 b 的偏导数（梯度），然后沿梯度的反方向调整 m 和 b ；外层迭代执行梯度下降法，逐步逼近偏导数等于0的点。
  其中需要注意偏导数的近似计算公式，已知误差函数

E(m,b)=1N⋅∑i=0N[yi−(m⋅xi+b)]2 E ( m , b ) = 1 N ⋅ ∑ i = 0 N [ y i − ( m ⋅ x i + b ) ] 2

  即各点与拟合直线的距离的平方和，再做算术平均。然后可以计算偏导数为

∂E∂m=−2N⋅xi⋅∑i=0N[yi−(m⋅xi+b)]∂E∂b=−2N⋅∑i=0N[yi−(m⋅xi+b)] ∂ E ∂ m = − 2 N ⋅ x i ⋅ ∑ i = 0 N [ y i − ( m ⋅ x i + b ) ] ∂ E ∂ b = − 2 N ⋅ ∑ i = 0 N [ y i − ( m ⋅ x i + b ) ]

  其中的求和公式在程序中表现为内层for循环
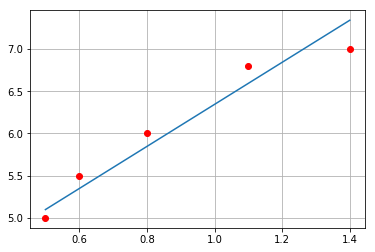
  下面再给出拟合后的效果图

import numpy as np
import matplotlib.pyplot as plt
a = np.array(wheat_and_bread)
plt.plot(a[:,0], a[:,1], 'ro')
b,m = gradient_descent_runner(wheat_and_bread, 1, 1, 0.01, 1000)
x = np.linspace(a[0,0], a[-1,0])
y = m * x + b
plt.plot(x, y)
plt.grid()
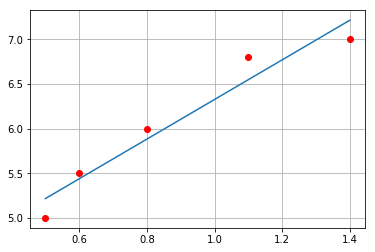
plt.show()

对比Numpy

import numpy as np
import matplotlib.pyplot as plt
a = np.array(wheat_and_bread)
plt.plot(a[:,0], a[:,1], 'ro')
m, b = np.polyfit(a[:,0], a[:,1], 1)
print([b,m])
x = np.linspace(a[0,0], a[-1,0])
y = m * x + b
plt.plot(x, y)
plt.grid()
plt.show()

[4.1072992700729891, 2.2189781021897814]