【笔记】程序正确性的证明

程序规约

程序功能的精确描述

1. 程序规约：对程序所实现功能的精确描述，
   由程序的前置断言和后置断言两部分组成。

2. 前置断言：程序执行前的输入应满足的条件，
   又称为输入断言。

3. 后置断言：程序执行后的输出应满足的条件，
   又称为输出断言。

程序规约的分类

非形式化程序规约

非形式化程序规约采用自然语言描述程序功能，简单、方便，但存在二义性，因此，不利于程序的正确性证明。

形式化程序规约

采用数学化的语言描述程序功能，描述精确，无二义性，便于程序的正确性证明。

Tips:书写程序规约

在书写程序规约时，使用Q表示前置断言，R表示后置断言，S表示问题求解的实现程序。在前置断言Q之前，还必须给出Q和R中所出现的标识符的必要说明。
例1：求数组b[0 : n-1]中所有元素的最大值。

[in n:integer; in b[0:n-1]:array of integer; out y:integer]
   Q: {n  ≥ 1}
          S
   R:{y ＝ MAX(i: 0 ≤ i ＜ n; b[i])}

例2：求两个非负整数的最大公约数。

         [in a,b :integer; out y:integer]
         Q: {a  ≥ 0 ∧ b  ≥ 0}
                S
         R:{y ＝ MAX(i: 1 ≤ i ≤min(a,b) ∧
              (a mod i ＝ 0) ∧ (b mod i ＝ 0))}

程序正确性

程序正确性的定义

衡量一个程序的正确性，主要看程序是否实现了问题所要求的功能。若程序实现了问题所要求的功能，则称它为正确的，否则是不正确的。

对程序的正确性理解，可以分为两个层次：

从广义来说，一个程序的正确性取决于该程序满足问题实际需求的程度。
从狭义而言，如果一个程序满足了它的程序规约就是正确的。

程序规约Q{S}R是一个逻辑表达式，其取值为真或假。

其中取值为真的含义是指：给定一段程序S，若程序开始执行之前Q为真，S的执行将终止，且终止时R为真，则称为 “程序S，关于前置断言Q和后置断言R是完全正确的”。

部分正确：

若对于每个使得Q(i)为真，并且程序S计算终止的输入信息i，R(i,S(i))都为真，则称程序S关于Q和R是部分正确的。

程序终止：

若对于每个使得Q(i)为真的输入i，程序S的计算都终止，则称程序S关于Q是终止的。

完全正确：

若对于每个使得Q(i)为真的输入信息i，程序S的计算都将终止，并且R(i,S(i))都为真，则称程序S关于Q和R是完全正确的。

一个程序的完全正确，等价于该程序是部分正确，同时又是终止的。

程序正确性证明的方法

证明部分正确性的方法
1. Floyd的不变式断言法
2. Manna的子目标断言法
3. Hoare的公理化方法

终止性证明的方法
1. Floyd的良序集方法
2. Knuth的计数器方法
3.Manna等人的不动点方法

完全正确性的方法
1. Hoare公理化方法的推广
2. Burstall的间发断言法
3. Dijkstra的弱谓词变换方法以及强验证方法

不变式断言法

循环不变式断言
把反映循环变量的变化规律，且在每次循环体的执行前后均为真的逻辑表达式称为该循环的不变式断言。

证明步骤：
1、建立断言
建立程序的输入、输出断言，如果程序中有循环出现的话，在循环中选取一个断点，在断点处建立一个循环不变式断言。
2、建立检验条件
将程序分解为不同的通路，为每一个通路建立一个检验条件，该检验条件为如下形式：
I ∧ R => O
其中I为输入断言，R为进入通路的条件，O为输出断言。
3、证明检验条件
运用数学工具证明步骤2得到的所有检验条件，如果每一条通路检验条件都为真，则该程序为部分正确的

实例：

例：设x,y为正整数，求x,y的最大公约数z的程序，即z=gcd(x,y)。

Function gcd(x1,x2:integer);
var y1,y2,z : Integer;
Begin
    y1:=x1;y2:=x2;
    while (y1!=y2) do
        if (y1>y2)
                y1:=y1-y2
            else 
                y2:=y2-y1
             z:=y1;
             write(z);                     
End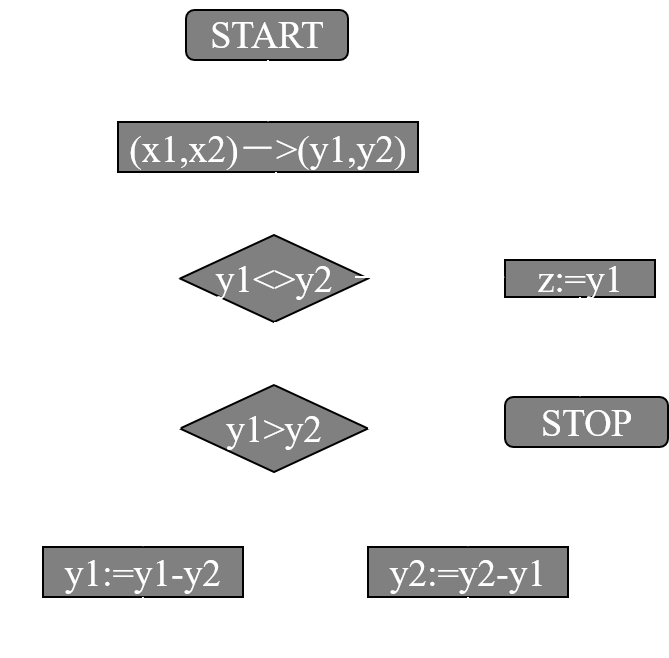

输入断言：

I(x1,x2): x1>0 ∧x2>0

输出断言：

O(x1,x2,z):z=gcd(x1,x2)

循环不变式断言：

P(x1,x2,y1,y2)：

x1>0 ∧ x2>0 ∧ y1>0 ∧ y2>0 ∧gcd(y1,y2)=gcd(x1,x2)

通路划分：
通路1：a->b
通路2：b->d->b
通路3：b->e->b
通路4：b->g->c

建立检验条件
检验条件： I ∧ R => O
通路1：

I(x1,x2)≥ P(x1,x2,y1,y2)

x1>0 ∧ x2>0 ≥ x1>0∧ x2>0 ∧ y1>0 ∧Y2>0 ∧ gcd(y1,y2)=gcd(x1,x2)

通路2：

P(x1,x2,y1,y2) ∧ y1≠y2 ∧ y1>y2 ≥ P(x1,x2,y1-y2,y2)

x1>0 ∧x2>0 ∧ y1>0 ∧ y2>0 ∧ gcd(y1,y2)=gcd(x1,x2) ∧ y1≠y2 ∧ y1>y2 ≥ x1>0 ∧ x2>0 ∧ y1-y2>0 ∧ y2>0 ∧ gcd(y1-y2,y2)=gcd(x1,x2)

通路3：

P(x1,x2,y1,y2) ∧ y1≠y2 ∧y10 ∧x2>0 ∧ y1>0 ∧ y2>0 ∧ gcd(y1,y2)=gcd(x1,x2) ∧ y1≠y2 ∧ y1 x1>0 ∧ x2>0 ∧ y1>0 ∧ y2-y1>0 ∧ gcd(y1,y2-y1)=gcd(x1,x2)

通路4：

P(x1,x2,y1,y2) ∧ y1=y2 ≥ O(x1,x2,z) x1>0 ∧x2>0 ∧ y1>0 ∧ y2>0 ∧ gcd(y1,y2) = gcd(x1,x2) ∧ y1 = y2 ≥ z=gcd(x1,x2)

证明检验条件
通路1： x1>0 ∧ x2>0 ∧ x1=y1 ∧ x2=y2 ≥……
通路2： 若y1>y2, gcd(y1-y2,y2) = gcd(y1,y2) =gcd(x1,x2)
通路3： 若y2>y1, gcd(y1,y2)=gcd(y1,y2-y1) =gcd(x1,x2)
通路4： 若y1=y2,gcd(y1,y2) =gcd(x1,x2)=y1=y2=z P(x1,x2,y1,y2) ∧ y1=y2 ≥ O(x1,x2,z)

子目标断言法

子目标断言法与不变式断言法的主要区别是：

• 两种方法对循环所建立的断言不同。
  不变式断言描述了程序变量y的中间值与初始值之间关系；
  子目标断言法描述的是y的中间值与循环终止时的最终值yend之间的关系。
• 两种方法进行归纳的方向不同。
  不变式断言沿着程序正常执行的方向进行归纳；
  子目标断言法则沿着相反方向进行归纳。

.
.
.
.
.
.
未完待续