matlab:光场传输的各种算法
随着计算机的飞速发展,数值仿真在许多光学领域都有重要的应用。比如:
1、在研究超分辨时需得到光场经特定结构后精确的聚焦情况
2、研究激光相干合束时需计算阵列光束远场合束光斑的能量分布情况
3、在设计衍射光学元件时需循环计算光场经衍射元件后的远场分布
4、在设计激光谐振腔时需计算腔内光束经过多次反射后的稳定光场分布
在这些研究中,普遍包含光场传输这一最基本的物理过程,因此研究光场传输快速、准确的实现方法具有重要意义。
目前,关于光场传输的算法,主要有两种:
1、基于菲涅尔衍射积分公式的离散化求和,即积分算法
优点:直观,易实现,计算结果准确
缺点:计算速度慢
2、快速傅里叶变换算法(FFT)
优点:计算速度快
缺点:不能得到较为精细的光场分布
3、矩阵相乘算法
优点:计算速度快,并且可以得到准确的光场分布
这里我们使用论文中所述的矩阵相乘算法。
该论文的matlab实现:
clc
close all
clear all
%% 光源部分
No = 200; %取样点数
N = 128;
lambda = 1064e-6; %波长1064nm
k = 2*pi/lambda; %波矢
w = 3; %高斯光束的束宽
d = 1000; %传输距离1000mm
[x0,y0] = meshgrid(linspace(-1.5*w,1.5*w,No));
E0 = exp(-(x0.^2+y0.^2)/w^2); %高斯光束
I0 = E0.*conj(E0); I0 = I0/max(max(I0));
figure;mesh(x0,y0,I0)
set(gca,'fontname','times new roman','fontsize',16); %设置图形对象属性
xlabel('x/mm','fontname','times new roman','fontsize',16);
ylabel('y/mm','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
%% 光传输矩阵相乘算法
dx0 = x0(1,2)-x0(1,1); dy0 = dx0;
[x1,y1] = meshgrid(linspace(-1.5*w,1.5*w,N));
Mx = exp(-1i*k/d*x1(1,:)'*x0(1,:));
My = exp(-1i*k/d*y0(:,1)*y1(:,1)');
M = E0.*exp(1i*k/2/d*(x0.^2+y0.^2));
E1 = -1i/lambda/d*exp(1i*k*d)*exp(1i*k/2/d*(x1.^2+y1.^2)).*(Mx*M*My);
I1 = E1.*conj(E1); I1 = I1/max(max(I1));
figure;mesh(x1,y1,I1);
set(gca,'fontname','times new roman','fontsize',16); %设置图形对象属性
xlabel('x/mm','fontname','times new roman','fontsize',16);
ylabel('y/mm','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
%% 积分算法
for a = 1:N
for b = 1:N
E2(a,b) = -1i/lambda/d*exp(1i*k*d)*sum(sum(E0.*exp(1i*k/2/d*((x1(a,b)-x0).^2+(y1(a,b)-y0).^2))));
end
a
end
I2 = E2.*conj(E2); I2 = I2/max(max(I2));
figure;mesh(x1,y1,I2)
set(gca,'fontname','times new roman','fontsize',16);
xlabel('x/mm','fontname','times new roman','fontsize',16);
ylabel('y/mm','fontname','times new roman','fontsize',16);
zlabel('归一化强度','fontname','华文中宋','fontsize',16);
运行结果:
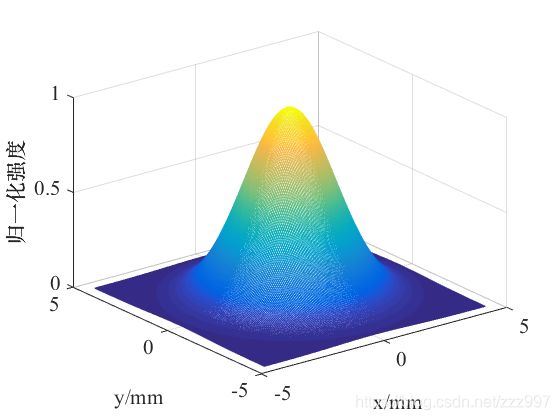
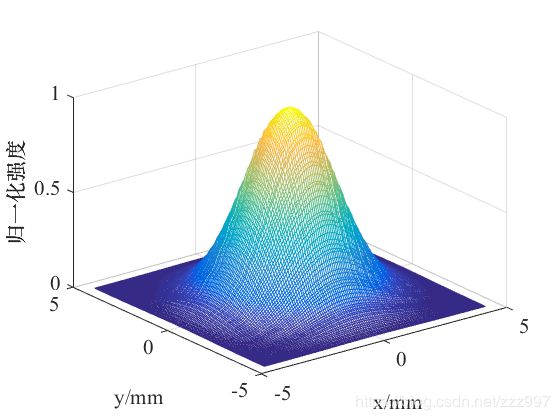

参考文献:
[1]龚海龙, 李国俊, 陈琪, et al. 一种快速实现光场传输的算法研究[J]. 光学学报, 2016, v.36;No.409(04):60-64.