说点积之前,先回顾一下我们之前对余弦定理的应用。
已知m、o、n 三点,求∠nom
1.将点o 归零
m.x-=o.x;
m.y-=o.y;
n.x-=o.x;
n.y-=o.y;
2.求cos(∠nom) 的值
const dot=(m.x*n.x+m.y*n.y);
const len=Math.sqrt(m.x*m.x+m.y*m.y)*Math.sqrt(n.x*n.x+n.y*n.y);
const cosTheta=dot/len;
上面的cosTheta 就是cos(∠nom) 的值。
3.使用反余弦方法acos() 从cos(∠nom)解析出∠mon
const theta=Math.acos(cosTheta);
cos(∠nom) 中的∠mon 和最后解析出来的∠mon 可能是不一样的,解析出的∠mon 会在[0,Math.PI] 之间,如:
Math.acos(Math.cos(-Math.PI)) === 3.141592653589793
接下来咱们就说一下上面第2步中,cosTheta=dot/len 是怎么来的,这得先从点积公式说起。
点积公式
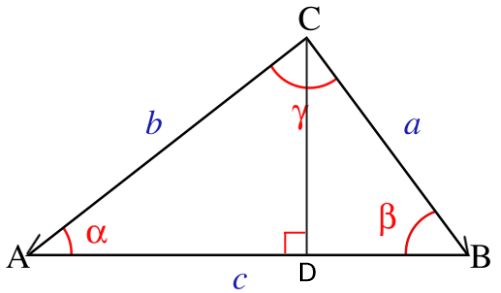
已知向量CA=b=(ax,ay)、CB=a=(bx,by),C为零点,∠ACB=γ
一,基本公式
1.由点积公式得:
a*b=|a|*|b|*cosγ,cosγ=(a*b)/(|a|*|b|)2.由点位乘积得:
a*b=ax*ax+by*by注:
- a、b、c 都是向量,|a| 代表向量a 的长度
- a*b 的值是一个实数,可正、可负、可零
由上面的点积公式和点位乘积公式可以看出,|a|*|b|*cosγ和ax*ax+by*by 是一样的,解下来我们就论证一下这个等式。
二,用勾股定理论证点积公式和点位乘积公式的相等
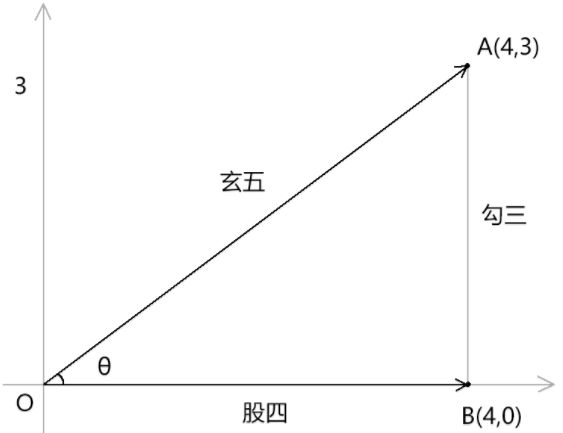
由点积公式 a*b=|a|*|b|*cosγ 得:
a*b=|OA|*|OB|*cosθ=5*4*cosθ=20*cosθ由三角函数余弦函数得:
cosθ=|AB|/|OA|=4/5将cosθ 的值代入点积公式得:
a*b=20*(4/5)=80/5=16由点位乘积公式a*b=ax*ax+by*by 得:
a*b=4*4+3*0=16由上可知点积公式和点位乘积的结果都是一样的
所以:点积公式和点位乘积公式相等
对于点积公式是怎么来的,我们还可以用余弦定理来推导
余弦定理
一,余弦定理和公式
1.余弦定理:对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
2.余弦公式:
c²=a²+b²-2*|a|*|b|*cosγ
3.同向量的相乘
c²、a²、b² 是同向量相乘的意思,其结果是向量长度的平方,如:
c²=c*c
=|c|*|c|*cos0
=|c|*|c|
二,余弦定理的推导
1.因为c 边的长度可以看成AD和DB的和,所以:
|c|=|a|*cos(β)+|b|*cos(α)
把等号两边都乘以c,得:
c²=|a|*|c|*cos(β)+|b|*|c|*cos(α)
同理:
a²=|a|*|c|*cos(β)+|a|*|b|*cos(γ)
b²=|b|*|c|*cos(α)+|a|*|b|*cos(γ)
2.a²和 b²两两相加,得:
a²+b²=|a|*|c|*cos(β)+|a|*|b|*cosγ+|b|*|c|*cos(α)+|a|*|b|*cosγ
从中分析可以发现:|a|*|c|*cos(β)+|b|*|c|*cos(α) 正好等于 c²
所以:把c²代入上式中,得:
a²+b²=c²+|a|*|b|*cosγ+|a|*|b|*cosγ
a²+b²=c²+2*|a|*|b|*cosγ
把c²作因变量,可得余弦公式:
c²=a²+b²-2*|a|*|b|*cosγ
3.有了余弦定理,我们就可以推导点积公式:
a*b=|a|*|b|*cosγ
因为:
c²=(a-b)²=(b-a)²所以:
(a-b)²=b²+a²-2*|b|*|a|*cosγ
a²-2*a*b+b²=b²+a²-2*|b|*|a|*cosγ
-2*a*b=-2*|b|*|a|*cosγ
a*b=|b|*|a|*cosγ
cosγ=(a*b)/(|a|*|b|)
注:a*b 是向量的相乘,|b|*|a| 是向量长度相乘;a*b的结果可正、可负、可零,|b|*|a| 的结果大于等于零。
接下来,就会到本章的起点了~
四,利用点积公式求余弦的值
用js 把向量中的点位解开,得:
a*b=ax*bx+ay*by
|a|=Math.sqr(ax*ax+ay*ay)
|b|=Math.sqr(bx*bx+by*by)
cosγ=(ax*bx+ay*by)/(Math.sqr(ax*ax+ay*ay)*Math.sqr(bx*bx+by*by))