图论——因子分解
因子分解相关概念
1、因子分解是图分解的一种方法
2、图G的因子 G i G_i Gi,指至少包含G的一条边的生成子图
(生成子图:包含原图所有顶点,边不管,若边数为m,则不同的生成子图有 2 m 2^m 2m个,不同的生成子图≠不同构)
3、图G的因子分解:指将G分解为若干边不重的因子之并
4、图G的n因子:指G的n度正则因子
5、若图G可以分解为若干n因子之并,称G是可n因子分解的

一、图的一因子分解
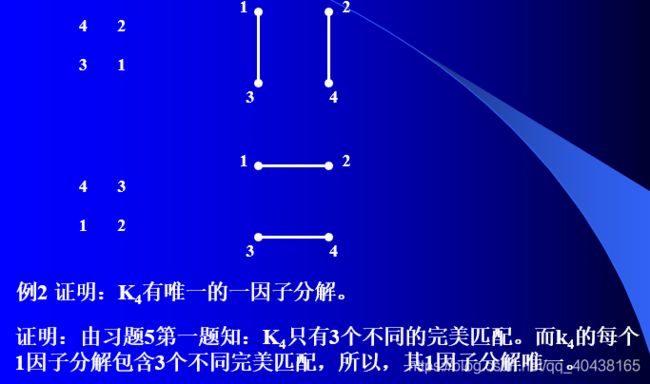
\quad 图的一个一因子实际上就是图的一个完美匹配的导出子图。一个图能够作一因子分解,也就是它能够分解为若干边不重的完美匹配的导出子图之并。
定理1: K 2 n K_{2n} K2n可一因子分解

推论:每个k(k>0)正则偶图G是一可因子分解的
证明: 证明:因为每个k (k>0)正则偶图G存在完美匹配,设Q是它的一个一因子,则G-Q还是正则偶图,由归纳知,G可作一因子分解。
定理2:具有H圈的3正则图可一因子分解
证明:从三正则图中抽取H圈,显然剩下的边构成G的一个一因子,而H圈是偶圈,可分解为两个一因子。故G可分解为三个一因子。
定理3:若三正则图有割边,则它不能一因子分解
证明:假设G的三个一因子为 G 1 , G 2 , G 3 G_1, G_2, G_3 G1,G2,G3,假设割边 e ∈ G 1 e\in G_1 e∈G1。显然, G − G 2 G-G_2 G−G2的每个分支必为圈。故e在G的某个圈中,这与e是G的割边矛盾。
note:没有割边的三正则图可能也没有一因子分解,如彼得森图就是如此!尽管它存在完美匹配。
二、图的二因子分解
\quad 如果一个图可以分解为若干2度正则因子之并,称G可以2因子分解。注意:G的一个H圈肯定是G的一个2因子,但是G的一个2因子不一定是G的H圈。2因子可以不连通。举个例子

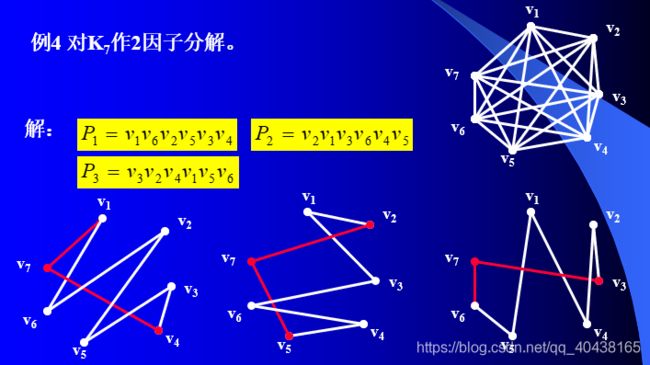
定理1: K 2 n + 1 K_{2n+1} K2n+1可2因子分解
证明:作图法证明之。作路 P i = v i v i − 1 v i + 1 v i − 2 v i + 2 v i − 3 ⋯ v i − n v i + n , i = 1 , 2 , ⋯ , n P_i=v_iv_{i-1}v_{i+1}v_{i-2}v_{i+2}v_{i-3} \cdots v_{i-n}v_{i+n}, i=1,2,\cdots,n Pi=vivi−1vi+1vi−2vi+2vi−3⋯vi−nvi+n,i=1,2,⋯,n,坐标需mod(2n)。n个生成圈为 v 2 n + 1 v_{2n+1} v2n+1与 P i P_i Pi两个端点连线。举个例子:
定理2: K 2 n K_{2n} K2n可分解为一个1因子和n-1个2因子之和
定理3:没有割边的3正则图是一个1因子和一个2因子之和
证明:因每个没有割边的3正则图存在完美匹配M,显然,G-M是2因子
定理4:一个连通图可2因子分解当且仅当它是偶数度正则图。
证明:当G是n阶2正则图时,G本身是一个2因子。设当G是n阶2k正则图时,可以进行2因子分解。当G是n阶2k+2正则图时,由1891年彼得森证明过的一个结论:顶点度数为偶数的任意正则图存在一个2因子Q。所以,G-Q是2k阶正则图。由归纳假设,充分性得证。
三、图的森林因子分解
\quad 把一个图分解为若干边不重的森林因子的和,称为图的森林因子分解。我们关注点在于将图G分解为边不重的森林因子的最少数目问题,称这个最少数目为G的荫度,记为σ(G)。
定理1:图G的荫度为 σ ( G ) = m a x [ m s s − 1 ] , s = 2 , 3 , ⋯ , n σ(G)=max[\frac{m_s}{s-1}], s=2,3,\cdots,n σ(G)=max[s−1ms],s=2,3,⋯,n,其中s是G的子图 H s H_s Hs的顶点数, m s = m a x { E ( H s ) } m_s=max\{E(H_s)\} ms=max{E(Hs)}。


定理2: σ ( K n ) = [ n / 2 ] , σ ( K r , s ) = [ r s r + s − 1 ] σ(K_n)=[n/2], σ(K_{r,s})=[\frac{rs}{r+s-1}] σ(Kn)=[n/2],σ(Kr,s)=[r+s−1rs] 都是向上取整
证明1:若n是偶数,且 δ ( G ) ≥ n 2 + 1 \delta(G)\ge\frac{n}{2}+1 δ(G)≥2n+1,则n阶图G有3因子。
因 δ ( G ) ≥ n 2 + 1 \delta(G)\ge\frac{n}{2}+1 δ(G)≥2n+1且n为偶数,由狄拉克定理可得G由H圈C,且C为偶圈,于是C可为G的两个1因子,设其中一个为F1。令G1=G-F1,则 δ ( G ) ≥ n 2 \delta(G)\ge\frac{n}{2} δ(G)≥2n,可得G1中有H圈C1,作H=C1∪F1.显然H是G的一个3因子。
证明:一棵树G有完美匹配当且仅当对所有顶点 v ∈ V ( G ) v \in V(G) v∈V(G),有: o ( G − v ) = 1 o(G-v)=1 o(G−v)=1
证明:每个2k(k>0)正则图是2可因子分解的。