图论--拓扑排序及其应用
在工程实践中,一个工程项目往往由若干个子项⽬目组成。这些子项目间往往有两种关系:
1 先后关系,即必须在某个项 ⽬完成后才能开始实施另一个子项目;
2 子项⽬目间无关系,即两个子项目可以同时进行,互不影响。
工厂里产品的生 产线上,一个产品由若干个零部件组成。零部件生产时,也存在这两种关系:先后关系,即一个部件必须在完成后才能生 产另一个部件;部件间无先后关系,即这两个部件可以同时生产。
大学里某个专业的课程学习,有些课程是基础课,它们 可独立于其他课程,即无前导课程;有些课程必须在某些基础看成是一个个顶点,课程的学习分别构成一个有向图,现在 要从这些有向图上分别找出的实施,产品的生产,课程的学习分别构成一个有向图,现在要从这些有向图上分别找出一个 施工流程图、产品生产流程图、课程学习流程图,以便顺利进行施工、产品生产和课程学习,解决这个问题可以采用拓扑 排序的方法。 设G=(V,E)是一个具有n个顶点的有向图,V中顶点的序列V1,V2,Vn称为⼀拓扑序列,当且仅当该顶点序列 满⾜足下列条件:若在有向图G中,从顶点Vi到是j有一条路径,则在序列中顶点必须排在顶点V之前。找一个有向图的一个拓扑序列的过程称为拓扑排序。
假定计算机软件专业的课程之间存在下述关系:
课程代号 课程名称 前导课程
C1 ⾼高等数学 无
C2 程序设计语⾔言 无
C3 数据结构 C2
C4 编译原理 C2,C3
C5 操作系统 C3,C6
C6 计算机组成原理 C7
C7 普通物理 C1
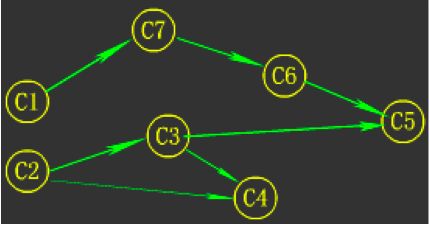
课程之间的先后关系可⽤用有向图表⽰示,如图所示。
对这个有向图进⾏行拓扑排序可得到⼀一个拓扑序列:C1,C2,C7,C6,C3,C4,C5。也可得到另⼀一个拓扑序列C1, C7,C2,C3,C6,C4,C5。学⽣生按照任何⼀一个拓扑序列都可以顺利地进⾏行课程学习。下⾯面给出有向图拓扑排序算法的基本步骤:
1 从图中选择⼀一个⼊入度为0的顶点,输出该顶点;
2 从图中删除该顶点及其相关联的弧;
3 重复执⾏行1、2直到所有顶点均被输出,拓扑排序完成或者图中再也没有⼊入度为0的顶点(此种情况说明原有向图含有环)。 可以证明,任何一个无环有向图,其全部顶点都可以排成一个拓扑序列。而且其拓扑序列不一定是唯一的。 下⾯以下图为例说明拓扑排序过程。
(a)邻接表 (b)有向图
首先C1、C4的入度都为0,选C1,删除C1及其边e1、e2,调整C2的⼊入度为0,C3的⼊入度为1,此时C2、C4的⼊入度为0 ,选C4,删除C4及边e3、e4,调整C3、C5的⼊入度为0,从C2、C5、C3中选C2,删除C2及边e,调整C6的⼊入度为2,从C3 、C5中选择C3,删除C3及边e6,调整C6的⼊入度为1,删除C5及边e7,调整C6的⼊入度为0,输出C6,⾄至此拓扑排完成,拓 扑序列为C1,C4,C2,C3,C5,C6。
这里拓扑排序给出两种方法:
1: 以邻接表作存储结构,给出拓扑排序的实现。算法设置一个队列(方便使用优先队列,输出相同条件下结点编号小的在前(后)的序列),将所有⼊入度为0的顶点入该队。找入度为0的 顶点,只要从依次出队即可。删除边的操作转化为将为该顶点为弧尾,所有相应弧头的入度减1。
2:类似于dfs 用一个栈来存排序后的顺序,从一个顶点开始访问,依次访问它的邻接顶点,回溯的时候将当前结点压入栈(度为0的顶点一定是最后压入栈的)
下面以poj 2376为例
输入n 表示n个结点;
从第一个结点开始依次输入该结点的邻接结点,输入0表示改结点的邻接结点结束,开始输入下一个结点的邻接结点。
#include
#include
#include
#include
#include
using namespace std;
struct node
{
int v;
int next;
}e[505];
int head[505]; //邻接表头
int indegree[505],n,m; //顶点入度统计数组
bool vis[505];
stacks;
void topologicalSort1()
{
queueq;
for (int i=1; i<=n; i++)
{
if(indegree[i]==0)
{
q.push(i);
}
}
bool flag=false;
while (!q.empty())
{
int t;
t=q.front();
q.pop();
if(flag)
{
printf(" %d",t);
}
else
{
printf("%d",t);
flag=true;
}
for (int i=head[t]; i!=-1; i=e[i].next)
{
indegree[e[i].v]--;
if(indegree[e[i].v]==0)
{
q.push(e[i].v);
}
}
}
printf("\n");
}
void dfs(int u)
{
vis[u]=true;
for (int i=head[u]; i!=-1; i=e[i].next) //尝试访问结点u的邻接结点
{
if(!vis[e[i].v])
{
dfs(e[i].v);
}
}
s.push(u); //在递归出口加入此结点
}
void topologicalSort2()
{
memset(vis, false, sizeof(vis));
while (!s.empty())
{
s.pop();
}
for (int i=1; i<=n; i++) //尝试访问每一个结点
{
if(!vis[i])
{
dfs(i);
}
}
int ans=1;
while (!s.empty()) //输出序列
{
if(ans 如果只是判断环是否存在那就更简单了,用dfs或者并查集都可以
//拓扑排序判环
#include
#include
#include
using namespace std;
#define MAX 100001
int head[MAX]; // 表示头指针,初始化为-1
int p[5*MAX]; // 表示指向的节点
int Next[5*MAX]; // 模拟指针,初始化为0
int n,m,u,v;
int vis[MAX]; //记录遍历的状态
bool flag;
bool dfs(int u)
{
vis[u]=-1; //正在访问,在递归栈中
for (int i=head[u]; i!=-1 && !flag; i=Next[i])
{
v=p[i];
if (vis[v]==-1)
{
flag=true;
return flag;
}
if (vis[v]==0) //没有访问过
{
vis[v]=-1;
dfs(v);
}
vis[v]=1; //访问结束
}
vis[u]=1;
return flag;
}
int main()
{
int t,cnt;
scanf("%d",&t);
while (t--)
{
cnt=0;
memset(head, -1, sizeof(head));
memset(vis, 0, sizeof(vis));
flag=false;
scanf("%d%d",&n,&m);
for (int i=0; i 应用:
描述
小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论,当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中,小Hi和小Ho整理得到了以下的信息:
- 校园网主干是由N个节点(编号1..N)组成,这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v,则节点u可以向节点v发送信息,但是节点v不能通过该链接向节点u发送信息。
- 在刚感染病毒时,校园网立刻切断了一些网络链接,恰好使得剩下网络连接不存在环,避免了节点被反复感染。也就是说从节点i扩散出的病毒,一定不会再回到节点i。
- 当1个病毒感染了节点后,它并不会检查这个节点是否被感染,而是直接将自身的拷贝向所有邻居节点发送,它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
- 现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。
举个例子,假设切断部分网络连接后学校网络如下图所示,由4个节点和4条链接构成。最开始只有节点1上有病毒。
![]()
最开始节点1向节点2和节点3传送了病毒,自身留有1个病毒:
![]()
其中一个病毒到达节点2后,向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝:
![]()
当从节点2传送到节点3的病毒到达之后,该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒:
![]()
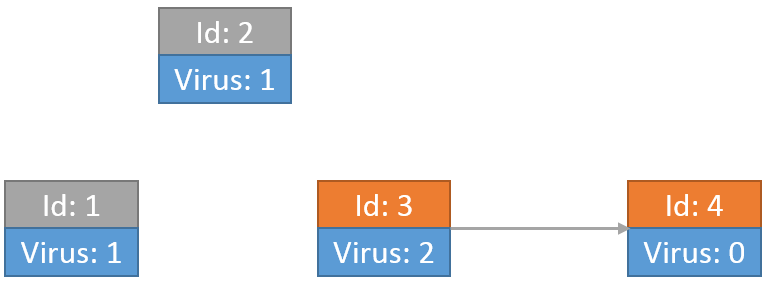
最后每个节点上的病毒为:
![]()
小Hi和小Ho根据目前的情况发现一段时间之后,所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说,最后会有多少个病毒呢?
输入
第1行:3个整数N,M,K,1≤K≤N≤100,000,1≤M≤500,000
第2行:K个整数A[i],A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N
第3..M+2行:每行2个整数 u,v,表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N
输出
第1行:1个整数,表示最后整个网络的病毒数量 MOD 142857
4 4 1 1 1 2 1 3 2 3 3 4样例输出
6
小Hi:对于这个问题小Ho你有什么想法么?
小Ho:有,对于一个病毒来说它总会传递到一个没有邻居的节点,那我直接使用dfs模拟整个过程不就能够得到结果了吗?
小Hi:小Ho你真聪明,立刻就看穿了这个问题的本质。
小Ho:那当然啦。<得意>
小Hi:那么小Ho,我这里有这样一个网络:
这里一共有n个节点,对于节点i,它总是连接着节点i+1和节点i+2。一开始只有节点1被感染,你算算最后n个节点一共有多少个病毒?
小Ho:很显然,节点1最后只有1个病毒;节点2也只有1个病毒;节点3会接受从节点1和节点2过来的病毒,所以有2个病毒;后面依次是节点4有3个病毒,节点5有5个病毒…它们好像刚好是费波拉契数列?
小Hi:你说的没错。对于这个网络,编号为i的节点最后感染的病毒数量就是斐波拉契数列的第i项。而斐波拉契数列的增长是很惊人的,当i到达一定值时,其电脑感染的病毒数量就会很大了。
小Ho:那这又有什么关系呢?反正能得到解不是么?
小Hi:能得到解那是当然了,但是你有想过需要花费多少时间么?在你的dfs算法中,每一次进入函数就等于模拟一个病毒进入电脑。如果最后结果有10亿个病毒,那么你就需要执行10亿次函数,假设电脑每秒钟可以执行1亿次函数,那么你的dfs就需要运行10秒。如果结果有100亿,1000亿呢?
小Ho:运行时间上好像是有问题,那我应该如何解决时间的问题呢?
小Hi:其实也很简单啦。你再想想,在我们最后得到结果上每各节点病毒数量有什么关系么?
小Ho:嗯<思考>…我发现了!对于节点i来说,它最后的病毒数好像总是等于所有能够达到它的节点病毒数之和。就用你提到的那个斐波拉契数列来说,能够达到节点i的节点是节点i-1和节点i-2,所以节点i的病毒数是节点i-1和节点i-2的病毒数之和。这刚好就是斐波拉契数列的递推公式嘛!
小Hi:对,正是这样。对于一个节点i来说,如果我们能够先计算出它所有前驱节点的病毒数量,就可以直接推算出它最后的病毒数量了。
小Ho:但是怎么来计算所有前驱节点呢?
小Hi:这就要从图的性质入手了。我们现在的网络是没有环的,对于任意一个节点i,当它将自己所有的病毒都传送出去之后,它自身的病毒数量就不会改变了。那么我们不妨从没有前驱节点,也就是入度为0的节点开始考虑。
对于这些节点,它并不会再增加病毒数量。那么我们就根据它所关联的连接将病毒分发出去,然后这个节点就没有作用了。那不妨就删掉好了,它所关联的边也删掉。
这样图中又会产生一些新的没有入度的节点。这样一直删点,直到所有的点都被删掉,将所有点的病毒数量加起来不就是总的病毒数么?
我们不妨来看个例子,这里给定一个网络:
![]()
最开始只有节点1是入度为0的点,所以将它的病毒传送,然后删掉节点1:
此时节点2成为了入度为0的点,同样将其删掉:
此时节点3为入度为0的点,同样操作:
最后只剩下节点4,因为它并没有后续节点,所以病毒感染的过程也就结束了。
小Ho:这不就是拓扑排序么!因为拓扑排序可以在O(n+m)的时间解决,整个问题的时间也减少到了O(n+m),那么再多的节点数都不怕了!
小Hi:没错,这样我们就完美地解决了这个问题。你能实现它么?
小Ho:没问题,就交给我吧!<自信>
说得很明白了吧#include
#include
#include
using namespace std;
#define MAX 100001
int head[MAX]; // 表示头指针,初始化为-1
int p[5*MAX]; // 表示指向的节点
int Next[5*MAX]; // 模拟指针,初始化为0
int inDeg[MAX]; //各节点的入度
int ans[MAX];
int n,m,u,v;
void topoSort()
{
queueq;
for (int i=1; i<=n; i++)
{
if (inDeg[i]==0)
{
q.push(i);
}
}
while (!q.empty())
{
u=q.front();
q.pop();
for (int i=head[u]; i!=-1; i=Next[i])
{
v=p[i];
inDeg[v]--;
ans[v]+=ans[u]; //这里
ans[v]%=142857;
if (inDeg[v]==0)
{
q.push(v);
}
}
}
}
int main()
{
int cnt,k;
cnt=0;
scanf("%d%d%d",&n,&m,&k);
for (int i=0;i<=n; i++) //初始化
{
head[i]=-1;
inDeg[i]=0;
ans[i]=0;
}
int x;
for (int i=0; i