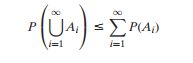《概率论基础教程》总结 -- 样本空间、概率、条件概率 等
一、排列组合
基本三个公式:
1、二项式系数
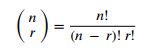
2、多项式系数

3、方程解的个数
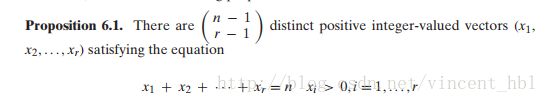
难度不大,解题中注意问题的转化。
二、样本空间
样本空间:考虑一个实验,所有可能结果构成的子集,称为该实验的样本空间。
这个定义就说明了样本空间的概率是1。
事件:样本空间的任意子集称为事件。
集合运算:
因为事件是集合,所以概率计算中就需要用到集合的各种运算,总结如下:
1、交并补
2、交换律、结合律、分配率。
3、德摩根定律。
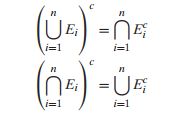
4、推演出的常用公式:
![]()
这个公式推广以后就可以说明全概率公式的正确性。
![]()
可以推广到更多个事件。
上面两个公式很有用,因为求并集的每个事件之间都是互斥的。
互斥事件
两个事件 E F 互斥(不相容),满足EF = 空集。也就是说两个事件不可能同时发生。
三、概率
笼统的讲,有两种概率。第一种是熟知的事件发生的相对频率取极限之后收敛的值。第二种是主观概率,是可信度的度量。
如果用数学语言来定义概率呢?
概率是定义在样本空间中的事件上的集函数,满足三个公理。
1、概率值非负,不大于1。
2、样本空间概率为1。
3、不相容事件并的概率,是每个事件概率的和。
概率的演算公式
1、包含关系
![]()
看起来简单,证明一下呢?
2、补集
![]()
3、交集(intersection)
事件交集的概率并不能从事件的概率求出来。除非事件是相互独立的。
概率的计算
一般直接计算事件概率的方法(不是从其他事件推理出),是统计事件包括的样本空间结果数量,除以样本空间所有结果的数量。这里有一个假设是,样本空间里每一个结果出现的概率是一样的。很多情况下,即是不说明,这个假设都应该是存在的。
目前,概率的计算就是算出两个排列组合的值,然后相除。后面的很多情况下,新的事件概率是从已知的概率推理出来的,这可以算两个不同的概率计算模式。
四、条件概率
条件概率相关的公式
1、条件概率的定义
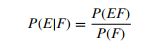
一个变化的公式也很常用
![]()
3、贝叶斯公式
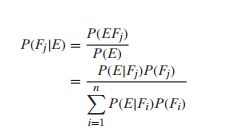
忘记机器学习里关于贝叶斯公式的东西,从简单的问题来理解贝叶斯公式。
假如有n个事件,每个事件记为Fj,这些事件的概率都已知。也就是P(Fj),这个被称为先验概率(就是最初的概率嘛)。
这种情况下,突然发生了一个事件E,此时要求E为条件的情况下Fj的概率,也就是后验概率。
考虑Fj是n个对同一个问题的不同假设(比如某人是否是癌症病人),每种假设有一个先验概率。当观察到一个事件E时,E能够对不同假设产生不同效果(比如肺部有一大片阴影这个事件会提高病人得了癌症的概率)。所以E也叫做证据。根据证据我们就可以修正原来假设的概率,修正后的概率就是后验概率。
简单说,贝叶斯公式是根据观察到的证据修正假设的概率的方法。
举个例子说明概率修正的意思。你去买彩票,中头奖的概率是已知的吧。开奖那天你无意中知道除了最后一个数字外,你买的彩票和头奖的开奖结果一模一样。这时,你对中头奖的预期就被大大提高了。这就是已知的证据修正了你对是否中头奖这个问题的假设的概率。
4、优势比
事件A发生的概率和A不发生的概率的比值是事件A的优势比。
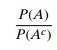
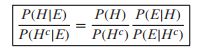
这个公式可以认为是证据修正事件优势比的公式。由贝叶斯公式推出。
5、全概率公式

其中Fi两两之间是不相容的。这就是贝叶斯公式等号右边的分母的部分。
独立事件
从上面贝叶斯公式的讨论中知道,证据事件E会修正已有事件F的概率,也就是说P(F | E)一般不等于P( F )。如果E不能对F产生影响的话,那么就认为E,F两个事件是独立的。有公式:
P( F | E ) = P( F )
换种表达:
![]()
概率独立性重要的原因在于很多的试验由一连串的重复试验组成的,试验之间彼此相同且相互独立的,也就是独立同分布。独立事件的定义保证了在计算一个独立同分布的重复试验的结果时,可以由每个事件的概率的乘积得到。
条件概率满足概率的所有定义
条件概率的定义满足概率的三个公理,在给定条件的情况下,事件的条件概率就是一个概率。
有点废话的感觉,换作用公式表示:P(F | E) = Q( F )。就是说E为条件下F的概率可以看做另一个F的概率函数。这个函数Q满足概率的所有定义和演算公式。所以条件概率上也可以使用上述的概率演算公式。上述概率演算公式中,每一个概率表达式中,都添加一个相同的条件,就得到条件概率的演算公式了。
条件独立(条件概率的独立)
既然条件概率是一个概率了,当然也可以计算条件概率和拥有独立性。思路类似:
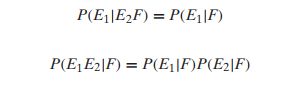
如果把条件F去掉,就成了普通的独立事件公式了。
另外验证条件概率的条件概率:
P( E1 | E2F ) = P( E1E2 | F ) / P( E2 | F )
看,如果把F条件去掉,是不是就成了普通的条件概率的公式。以上两个结论都证明了条件概率满足概率的所有定义这个事实。
五、难点
1、事件的互斥性和独立性。
关于两个事件的以下结论成立:
互不相容一定不独立
独立一定相容
PS:一个没想通的问题
命题:若P( A | B ) = 1,则B 属于A。该命题成立吗?如果不成立,正确的推论应该是什么呢?