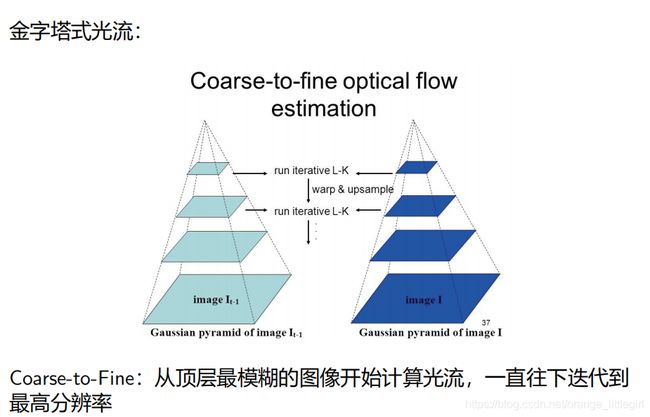
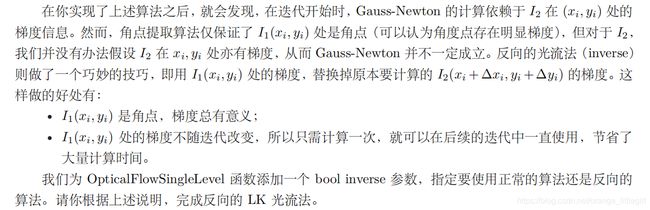
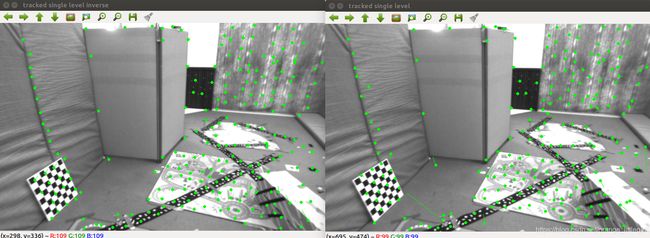
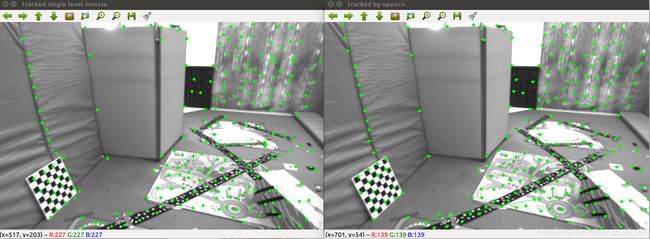
视觉slam14讲学习（七）之视觉里程计组成:光流法

1.简介

1.1光流基本知识

1.2光流分类

• 1.四种分类
  按算法分类，有两种分法: 一种可以分为迭加法或组合法（additive or compositional）;
  第二种是向前或者反向算法（forwards or inverse）.
  （有人翻译：叠加式(additive)和构造式(compositional)，前向(forwards)，逆向(inverse)）。
  从而导出四种图像对齐算法（all four image alignment algorithms），分别是 Forward Additive(FA),
  Forward Compositional(FC) 以 及 新 提 出 的 Inverse Compositional(IC) 算 法 , Inverse
  Additive(IA)算法。下表所示:
  
  有 3 中可选方案 alternative approaches 分别为：Compositional Image Alignment（补偿图像对齐）, Inverse Compositional Image Alignment（逆向补偿图像对齐）， Inverse Additive Image Alignment（逆向递增图像对齐)

• 2.前向和后向的区别
  向前方法对于输入图像进行参数化(包括仿射变换及放射增量). 反向方法则同时参
  数输入图像和模板图像, 其中输入图像参数化仿射变换, 模板图像参数化仿射增量. 因
  此反向方法的计算量显著降低.。由于图像灰度值和运动参数非线性, 整个优化过程为非
  线性。
  向前方法和反向方法在目标函数上不太一样，一个是把运动向量 p 都是跟着 I（被匹配图像），但是向前方法中的迭代的微小量 Δp 使用 I 计算，反向方法中的 Δp 使用 T计算，这样计算量便小了。

• 3.叠加和构造式的区别
  通过增量的表示方式来区分方法. 迭代更新运动参数的时候，如果迭代的结果是在原始的值(6个运动参数)上增加一个微小量，那么称之为Additive，如果在仿射矩阵上乘以一个矩阵(增量运动参数形成的增量仿射矩阵)，这方法称之为Compositional。两者理论上是等效的，而且计算量也差不多。

• 4.在 compositional 中，为什么有时候需要做原始图像的 wrap？该 wrap 有何物理意义？
  compositional 的两种 算法（Forward Compositional，Inverse Compositional）中，都需要在当前位姿估计之前引入增量式 warp（incremental warp）以建立半群约束要求（the semi-group requirement）。
  Forward Compositional 的 warp 集合包含 identity warp, warp 集 合 包 含 在Composition 操作上是半群(semi-group), 其中包括 Homograph, 3D rotation 等. Inverse Compositional 也是 semi-group, 另外要求增量 warp 可逆, 其中包括 Homograph, 3D rotation 等, 但不包括 piece wise affine.

3.光流法实战

3.1opencv版本

• 1.函数说明:
  void cv::calcOpticalFlowPyrLK (
  InputArray prevImg,
  InputArray nextImg,
  InputArray prevPts,
  InputOutputArray nextPts,
  OutputArray status,
  OutputArray err,
  Size winSize = Size(21, 21),
  int maxLevel = 3,
  TermCriteria criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01),
  int flags = 0,
  double minEigThreshold = 1e-4
  )
  
• 2.代码实战:

#include 
#include 
#include 
#include 
#include 
using namespace std; 

#include 
#include 
#include 
#include 

int main( int argc, char** argv )
{
    if ( argc != 2 )
    {
        cout<<"usage: useLK path_to_dataset"< keypoints;      // 因为要删除跟踪失败的点，使用list
    cv::Mat color, depth, last_color;
    
    for ( int index=0; index<100; index++ )
    {
        fin>>time_rgb>>rgb_file>>time_depth>>depth_file;
        color = cv::imread( path_to_dataset+"/"+rgb_file );
        depth = cv::imread( path_to_dataset+"/"+depth_file, -1 );
        if (index ==0 )
        {
            // 对第一帧提取FAST特征点,Harris角点
            vector kps;
//            cv::Ptr detector = cv::FastFeatureDetector::create();
             cv::Ptr detector = cv::GFTTDetector::create(200, 0.01, 20);//可以筛选个数,角点
             //之前角点检测的时候提到过角点检测的算法,第一个是cornerHarris计算角点,但是这种角点检测算法容易出现聚簇现象以及角点信息有丢失和位置偏移现象,
             //所以后面又提出一种名为 shi_tomasi的角点检测算法,名称goodFeatureToTrack,opencv的feature2D接口集成了这种算法,名称为GFTTDetector,接口如
            detector->detect( color, kps );
            for ( auto kp:kps )
                keypoints.push_back( kp.pt );
            last_color = color;
            continue;
        }
        if ( color.data==nullptr || depth.data==nullptr )
            continue;
        // 对其他帧用LK跟踪特征点
        vector next_keypoints; 
        vector prev_keypoints;
        for ( auto kp:keypoints )
            prev_keypoints.push_back(kp);
        vector status;
        vector error; 
        chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
        cv::calcOpticalFlowPyrLK( last_color, color, prev_keypoints, next_keypoints, status, error );
        chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
        chrono::duration time_used = chrono::duration_cast>( t2-t1 );
        cout<<"LK Flow use time："<

3.2手写单层G-N光流法

• 1.算法分析
  
• 2.单层LK代码实现

void OpticalFlowSingleLevel(
        const Mat &img1,
        const Mat &img2,
        const vector &kp1,
        vector &kp2,
        vector &success,
        bool inverse
) {

    // parameters
    int half_patch_size = 4;
    int iterations = 10;
    bool have_initial = !kp2.empty(); // !kp2.empty()意思是kp2不为空

    for (size_t i = 0; i < kp1.size(); i++) {
        auto kp = kp1[i];
        double dx = 0, dy = 0; // dx,dy need to be estimated
        if (have_initial) {
            dx = kp2[i].pt.x - kp.pt.x;
            dy = kp2[i].pt.y - kp.pt.y;
        }

        double cost = 0, lastCost = 0;
        bool succ = true; // indicate if this point succeeded

        // Gauss-Newton iterations
        for (int iter = 0; iter < iterations; iter++) {
            Eigen::Matrix2d H = Eigen::Matrix2d::Zero();
            Eigen::Vector2d b = Eigen::Vector2d::Zero();
            cost = 0;

            if (kp.pt.x + dx <= half_patch_size || kp.pt.x + dx >= img1.cols - half_patch_size ||
                kp.pt.y + dy <= half_patch_size || kp.pt.y + dy >= img1.rows - half_patch_size) {   // go outside
                succ = false;
                break;
            }

            // compute cost and jacobian
            for (int x = -half_patch_size; x < half_patch_size; x++)
                for (int y = -half_patch_size; y < half_patch_size; y++) {

                    // TODO START YOUR CODE HERE (~8 lines)
                    float p_x = kp.pt.x;
                    float p_y = kp.pt.y;
                    int k = x + y + 2 * half_patch_size;

                    double error = 0;
                    Eigen::Vector2d J;  // Jacobian
                    if (inverse == false) {
                        // Forward Jacobian by current frame
                        J[0] = GetPixelValue(img2, p_x + x, p_y + y) - GetPixelValue(img2, p_x + x - 1, p_y + y);
                        J[1] = GetPixelValue(img2, p_x + x, p_y + y) - GetPixelValue(img2, p_x + x, p_y + y - 1);
                    } else {
                        // Inverse Jacobian by previous frame
                        // NOTE this J does not change when dx, dy is updated, so we can store it and only compute error
                        J[0] = GetPixelValue(img1, p_x + x, p_y + y) - GetPixelValue(img1, p_x + x - 1, p_y + y);
                        J[1] = GetPixelValue(img1, p_x + x, p_y + y) - GetPixelValue(img1, p_x + x, p_y + y - 1);
                    }

                    // compute H, b and set cost;H=J^T*J
                    H += J * J.transpose();
                    error = GetPixelValue(img2, p_x + x+ dx, p_y + y + dy) - GetPixelValue(img1, p_x + x, p_y + y);
                    b += -error * J;
                    cost += error * error / 2;
                    
                    // TODO END YOUR CODE HERE
                }

            // compute update
            // TODO START YOUR CODE HERE (~1 lines)
            Eigen::Vector2d update;
            update = H.ldlt().solve(b);
            //cout << "update[dx,dy]_Cholesky_ldlt =" < 0 && cost > lastCost) {
                cout << "cost increased: " << cost << ", " << lastCost << endl;
                break;
            }

            // update dx, dy
            dx += update[0];
            dy += update[1];
            lastCost = cost;
            succ = true;
            //cout << "update dx,dy is :" <

• 3.总结:inverse法和forward法
  
  
• 4.实验结果:
  单层反向（左）和单层正向（右）：
  从结果来看反向法结果要明显优于正向法，特征点的位置和光流方向正确率都更高。
  

下图左图为单层反向法 ，右图为OpenCV 函数实现。

3.3手写多层G-N光流法

• 1.算法分析
  
• 2.代码实现

void OpticalFlowMultiLevel(
        const Mat &img1,
        const Mat &img2,
        const vector &kp1,
        vector &kp2,
        vector &success,
        bool inverse) {

    // parameters
    int pyramids = 4;
    double pyramid_scale = 0.5;
    double scales[] = {1.0, 0.5, 0.25, 0.125};

    // create pyramids
    vector pyr1, pyr2; // image pyramids
    // TODO START YOUR CODE HERE (~8 lines)

    cout<<"img1.size = "<> vec_kp1(pyramids, vector(kp1.size()));
    vector> vec_kp2(pyramids, vector(kp1.size()));
    //对第0层金字塔赋初值
    pyr1[0] = img1;
    pyr2[0] = img2;
    imshow("[pyr1[0]]",pyr1[0]);
    imshow("[pyr2[0]]",pyr2[0]);
    for (int j = 0; j < kp1.size(); j++) {
        vec_kp1[0][j].pt = kp1[j].pt*scales[0];
    }
    //思路：将传入的第一幅图kp2参数采的特征点赋值给第二层，第三层，第四层
    for (int i = 0; i < pyramids-1; i++) {//下采样,pyrDown,缩小图片大小
        //创建四层图像金字塔
        pyrDown(pyr1[i], pyr1[i+1], Size(pyr1[i].cols * pyramid_scale, pyr1[i].rows * pyramid_scale));
        pyrDown(pyr2[i], pyr2[i+1], Size(pyr2[i].cols * pyramid_scale, pyr2[i].rows * pyramid_scale));
        imshow("[pyr1]"+i,pyr1[i+1]);
        imshow("[pyr2]"+i,pyr2[i+1]);
        //将第一帧图像下一层的特征点坐标，乘以缩小倍数赋值给上一层//
        for (int j = 0; j < kp1.size(); j++) {
            vec_kp1[i+1][j].pt = kp1[j].pt*scales[i+1];
        }
    }
    // TODO END YOUR CODE HERE

    // coarse-to-fine LK tracking in pyramids
    // TODO START YOUR CODE HERE
    //创建四层金字塔图像关键点bool描述
    vector> vec_success_single(4);
    vector kp2_now;
    vector kp2_last(kp1.size());
    //将生成的第二帧特征点坐标赋值给下一层金字塔
    for (int k = pyramids - 1; k >= 0; k--) {
    OpticalFlowSingleLevel(pyr1[k], pyr2[k], vec_kp1[k], kp2_now, vec_success_single[k],inverse);
    //KeyPoint kp2_temp = vkp2_last[j];
        for (int j = 0; j < kp1.size(); j++) {
            kp2_last[j].pt = kp2_now[j].pt;
        }
        for (int j = 0; j < kp1.size(); j++) {
            kp2_now[j].pt = kp2_last[j].pt/pyramid_scale;
        }
        //测试参数是否传进来
        /*for (int l = 0; l < kp2_now.size(); l++) {
            cout << "第【" << k << " 】层kp2[" << l << "] = " << kp2_now[l].pt << endl;
            cout << "vec_success_single[" << l << "]" << vec_success_single[k][l] << endl;
        }*/
    }
    //下面测试图像金字塔尺度和特征点是否有误，调试用
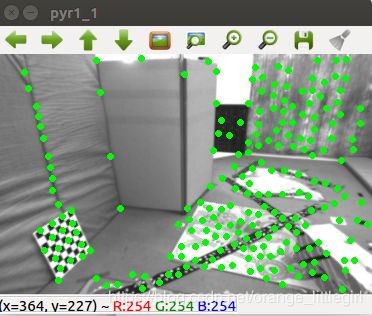
     Mat pyr1_1 = pyr1[1];//新构建一副图，在下文中将构建出来的画出来
    cv::cvtColor(pyr1_1, pyr1_1, CV_GRAY2BGR);
    for (int i = 0; i < vec_kp1[1].size(); i++) {
        if (vec_success_single[1][i]) {
            cout << "vec_kp1[1] = " << vec_kp1[1][i].pt << endl;
            cv::circle(pyr1_1, vec_kp1[1][i].pt, 2, cv::Scalar(0, 250, 0), 2);//在kp2的关键点位置画一个圈
            //cv::line(pyr1_3, kp1[i].pt, kp2_single[i].pt, cv::Scalar(0, 250, 0));//在kp1到kp2位置画一条线
        }
    }
    cv::imshow("pyr1_1", pyr1_1);
    //更新kp2，success，作为返回值
    kp2.resize(kp1.size());
    success.resize(kp1.size());
    for (int l = 0; l < kp1.size(); l++) {
        kp2[l].pt = kp2_last[l].pt;
        //cout << "kp2[" << l << "] = " << vec_kp1[3][l].pt << endl;
        success[l] = vec_success_single[0][l];
    }

    // TODO END YOUR CODE HERE
    // don't forget to set the results into kp2
}

• 3.实验测试
  
  金字塔，分四层，底层至上分别为 level0，level1，level2，level3.
  实验前，我在 level1 上做了特征点测试，显示缩小尺度之后关键点坐标尺度收缩正确。
  

参考:
总结：光流–LK 光流–基于金字塔分层的 LK 光流–中值:
https://blog.csdn.net/sgfmby1994/article/details/68489944
光流分类:
https://blog.csdn.net/wendox/article/details/525059