fyy2603
fyy2603

POJ 1475 Pushing Boxes

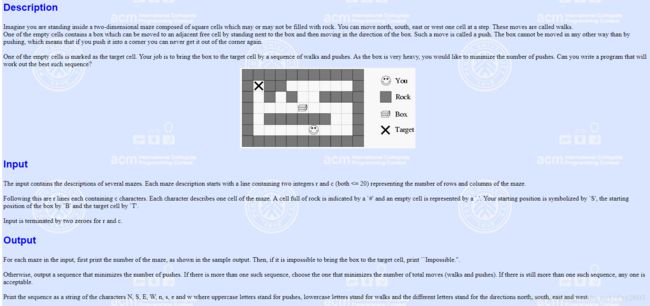
POJ 1475 Pushing Boxes_第1张图片


题意：

 给你一张地图，把箱子推到目的地，要求在推箱子次数最少的前提下最小化走的路程。输出方案。

题解：

 这题网上有很多A*和嵌套bfs的做法。事实上Dijkstra解决这道题也十分优越。

 用状态dis[a][b][c][d]表示人处于(a,b)这个点，箱子处于(c,d)这个点的最小费用。费用的定义是推箱子的费用+人行走

的费用。我们将一次推箱子的费用设置成10000，而人走一次的费用设置成1，就满足了在推箱子次数最少的前提下最小化

走的路程的条件。输出方案的话记录一下前驱节点即可。复杂度O(n^2*m^2*log(n^2*m^2))

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define LL long long
using namespace std;
const int N=22;
const int Cost=1e4+10;
const int inf=0x3f3f3f3f;
const int u[4]={1,0,-1,0};
const int v[4]={0,1,0,-1};
const char move[4]={'S','E','N','W'};

char s[N][N];
int n,m,a[N][N],las[N][N][N][N],dis[N][N][N][N],push[N][N][N][N];
int xb,yb,xe,ye,boxx,boxy;
struct Pnt {
	int a,b,c,d,dis;
};
struct cmp {
	bool operator () (const Pnt &x,const Pnt &y) {
		return x.dis>y.dis;
	}
};
priority_queue ,cmp> Q;

namespace FastIO {
	template inline void read(tp &x) {
		x=0; register char c=getchar(); register bool f=0;
		for(;c<'0'||c>'9';f|=(c=='-'),c = getchar());
		for(;c>='0'&&c<='9';x=(x<<3)+(x<<1)+c-'0',c = getchar());
		if(f) x=-x;
	}
	template inline void write(tp x) {
		if (x==0) return (void) (putchar('0'));
		if (x<0) putchar('-'),x=-x;
		int pr[20]; register int cnt=0;
		for (;x;x/=10) pr[++cnt]=x%10;
		while (cnt) putchar(pr[cnt--]+'0');
	}
	template inline void writeln(tp x) {
		write(x);
		putchar('\n');
	}
}
using namespace FastIO;

inline int Check(int x,int y) {
	if (a[x][y]!=1) return 0;
	if (x==0||x>n) return 0;
	if (y==0||y>m) return 0;
	return 1;
}

void Dijkstra() {
	dis[xb][yb][boxx][boxy]=0;
	Q.push((Pnt){xb,yb,boxx,boxy,0});
	while (!Q.empty()) {
		Pnt t=Q.top(); Q.pop();
		for (int i=0;i<4;i++) {
			if (Check(t.a+u[i],t.b+v[i])) {
				if (t.a+u[i]==t.c&&t.b+v[i]==t.d) {
					if (Check(t.c+u[i],t.d+v[i])) {
						int *r=&dis[t.c][t.d][t.c+u[i]][t.d+v[i]];
						if (*r>t.dis+Cost) {
							*r=t.dis+Cost;
							Q.push((Pnt){t.c,t.d,t.c+u[i],t.d+v[i],*r});
							las[t.c][t.d][t.c+u[i]][t.d+v[i]]=i;
							push[t.c][t.d][t.c+u[i]][t.d+v[i]]=1;
						}
					}
				}
				else {
					int *r=&dis[t.a+u[i]][t.b+v[i]][t.c][t.d];
					if (*r>t.dis+1) {
						*r=t.dis+1;
						Q.push((Pnt){t.a+u[i],t.b+v[i],t.c,t.d,*r});
						las[t.a+u[i]][t.b+v[i]][t.c][t.d]=i;
						push[t.a+u[i]][t.b+v[i]][t.c][t.d]=0;
					}
				}
			}
		}
	}
}

void output(int a,int b,int c,int d) {
	int t=las[a][b][c][d];
	if (~t) {
		if (push[a][b][c][d]) output(a-u[t],b-v[t],c-u[t],d-v[t]),putchar(move[t]);
		else output(a-u[t],b-v[t],c,d),putchar(move[t]-'A'+'a');
	}
}

void Solve() {
	Dijkstra();
	int ans=inf,x=0,y=0;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
			if (dis[i][j][xe][ye]


你可能感兴趣的:(图论)

  • 连通无向图一般中心的算法及其matlab程序详解 夏天天天天天天天# 图论算法matlab图论
    #################本文为学习《图论算法及其MATLAB实现》的学习笔记#################若服务点只允许取在各顶点上,而服务对象却取在各顶点及各边(或弧)上的点,则在所有顶点中选定一个顶点作为图的一般中心其条件是该点离它本身的最远服务对象(包括顶点及各边(或弧)上的点)的距离达到极小值。寻找无向图的一般中心对解决网络最佳服务点确定的问题是十分有效的，使得服务对象的范围
  • 大二上学期详细学习计划 学会沉淀。 学习
    本学习完成目标：项目：书籍：《mysql必知必会》《java核心技术卷》（暂时）加强JavaSE的学习，掌握Java核心Mysql+sql（把牛客上的那50道sql语句题写完）git+maven完成springboot项目（跟着黑马敲）对于每天的Java学习进行记录算法：刷题（多去刷cf上的题，每周15道）针对最近比赛薄弱的地方加强练习（图论，字符串，动态规划，搜索）cf先上1400，牛客和atc
  • 运筹学——图论与最短距离（Python实现）(2)，2024年最新Python高级面试framework m0_60575487 2024年程序员学习图论python面试
    适用于wij≥0，给出了从vs到任意一个点vj的最短路。Dijkstra算法是在1959年提出来的。目前公认，在所有的权wij≥0时，这个算法是寻求最短路问题最好的算法。并且，这个算法实际上也给出了寻求从一个始定点vs到任意一个点vj的最短路。2案例1——贪心算法实现==============2.1旅行商问题（TSP）**旅行商问题(TravelingSalesmanProblem，TSP)**
  • 图论篇--代码随想录算法训练营第五十八天打卡|拓扑排序，dijkstra（朴素版） 热爱编程的OP leetcode算法图论数据结构c++
    拓扑排序题目链接：117.软件构建题目描述：某个大型软件项目的构建系统拥有N个文件，文件编号从0到N-1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件A依赖于文件B，则必须在处理文件A之前处理文件B（0#include#include#includeusingnamespacestd;intmain(){intm,n,s,t;cin>>n>>m;vectorinDegree(n,0
  • 代码随想录算法训练营Day56|| 图论part06 傲世尊 图论
    卡玛网108冗余链接：每输入一条边，检查两个节点是否在同一集合中，如果已经在了，就说明这条边是多余的，直接输出。（如果加入这条边就一定成环了）卡玛网109冗余链接II：这题的复杂度直接上升了一百个档次，需要准备许多函数待调用。思路必须得极其清楚。第一遍看下来理解了，自己写肯定写不出来，需要看好几遍的题。
  • 五一的成果 王跃坤txdy
    emm。。五一过了有意义的四天。原来简单的图论我也是可以搞出来的原来DFS放进图论真的会使难度变大原来BFS在没有出口的时候会以超指数的爆炸增长原来二叉树并不是很难原来哈希的速度远超数组原来动态规划滚动起来速度真的快原来栈是那么的有用，可惜来不及学了（遇到一个求化学方程式的算法题，我自己写了133行的字符串处理，原来用栈可以缩减3倍的代码）原来很多复杂的问题都可以拆解成很简单的问题比如我好像发现数
  • 代码随想录训练营 Day58打卡 图论part08 拓扑排序 dijkstra(朴素版) 那一抹阳光多灿烂 图论力扣图论算法python数据结构
    代码随想录训练营Day58打卡图论part08一、拓扑排序例题：卡码117.软件构建题目描述某个大型软件项目的构建系统拥有N个文件，文件编号从0到N-1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件A依赖于文件B，则必须在处理文件A之前处理文件B（0<=A,B<=N-1）。请编写一个算法，用于确定文件处理的顺序。输入描述第一行输入两个正整数N,M。表示N个文件之间拥有M条依赖关系。
  • Leetcode 每日一题：Course Schedule II 南加第一划水 Leetcode每日一题leetcode算法职场和发展图论c++数据结构深度优先
    写在前面：今天我们继续来看一道经典的图论问题，而这个问题可以说是跟我们一众学生的生活息息相关啊！我们每年都有很多需要完成的必修指标，每一个必修指标可能会有一个或多个先修要求，而我们需要决定是否能将这些课全都上一遍，这不就是咱们苦逼大学生每学期选课前的日常嘛！那既然如此，我们就来看看这道与我们生活息息相关的这道算法题吧～～题目介绍：题目信息：题目链接：https://leetcode.com/pro
  • 图论中虚拟原点和反向建图两种方法—Acwing1137选择最短路线 kkj2004 算法图论
    虚拟原点和反向建图两种方法（本题中受范围限制运行速度区别不大）（附AC代码）这是蒟蒻在Acwing的第一篇题解（斗胆求赞）题目传送门现在时间是2023/1/2620:56，给大家拜个晚年看到题的第一眼就发现了这道题是一道图论中巧妙建图的模板题水题（好在范围也不大，不用加任何的优化）这道题如果一开始的思路是让某个图论算法跑W遍的话，那大概率会TLE（当然我没试），所以我们不能将这道题的时间复杂度*W
  • 搜索与图论 yy代码 图论深度优先算法
    第三章搜索与图论1.深度优先搜索DFS一条路走到黑数字全排列[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-g3u66CKm-1657019682316)(C:\Users\ZBY\Desktop\Snipaste_2022-06-22_18-43-39.png)]#includeusingnamespacestd;#include#includeintn;const
  • 【代码随想录训练营第42期 Day53打卡 - 图论Part4 - 卡码网 110. 字符串接龙 105. 有向图的完全可达性 逝去的秋风 代码随想录打卡图论深度优先算法广度优先
    目录一、个人感受二、题目与题解题目一：卡码网110.字符串接龙题目链接题解：BFS+哈希题目二：卡码网105.有向图的完全可达性题目链接题解：DFS三、小结一、个人感受对于两大基本搜索：深度优先搜索DFS遍历所有路径，每条路径都是一条路走到底，用于解决需要处理所有位置的情况；广度优先搜索BFS遍历最近相邻路径（常用邻接图，邻接表实现），用于用于求得最短路径，最小次数等。今天打卡题目个人感觉挺难，事
  • 【代码随想录训练营第42期 续Day52打卡 - 图论Part3 - 卡码网 103. 水流问题 104. 建造最大岛屿 逝去的秋风 代码随想录打卡算法深度优先图论
    目录一、做题心得二、题目与题解题目一：卡码网103.水流问题题目链接题解：DFS题目二：卡码网104.建造最大岛屿题目链接题解：DFS三、小结一、做题心得也是成功补上昨天的打卡了。这里继续图论章节，还是选择使用DFS来解决这类搜索问题（单纯因为我更熟悉DFS一点），今天补卡的是水流问题和岛屿问题。个人感觉这一章节题对于刚入门图论还是挺有难度的，我们需要搞清楚DFS函数的作用，以及具体的代码书写，然
  • 图论篇--代码随想录算法训练营第五十一天打卡| 99. 岛屿数量（深搜版），99. 岛屿数量（广搜版），100. 岛屿的最大面积 热爱编程的OP leetcode算法图论数据结构c++学习
    99.岛屿数量（深搜版）题目链接：99.岛屿数量题目描述：给定一个由1（陆地）和0（水）组成的矩阵，你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。解题思路：1、每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。2、遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。在遇到标记过的陆地节点和
  • java编程题——八皇后问题 sdg_advance java算法排序算法数据结构
    背景及问题介绍：八皇后问题（英文：Eightqueens），是由国际象棋棋手马克斯·贝瑟尔于1848年提出的问题，是回溯算法的典型案例。问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±9
  • 算法训练营|图论第9天 dijkstra(堆优化),bellman_ford 人间温柔观察者 算法图论
    题目：dijkstra(堆优化)题目链接：47.参加科学大会（第六期模拟笔试）(kamacoder.com)代码：#includeusingnamespacestd;classmycomparison{public:booloperator()(constpair&lhs,constpair&rhs){returnlhs.second>rhs.second;}};structEdge{intto;
  • 【图论】虚树 - 模板总结 Texcavator 图论图论
    适用于解决一棵树中只需要用到少部分点的时候，将需要用到的点提出来单独建一棵树/*********************虚树*********************/structedge{intto,next;intval;};structVirtual_Tree{intn;//点数intdfn[N];//dfs序intdep[N];//深度intfa[N][25],m[N];intnum;//
  • 图的邻接表建立方法和深搜广搜 翔山代码 算法深度优先算法
    深度优先搜索（DFS）和广度优先搜索（BFS）是图论中两种经典的图遍历算法，它们在解决各种问题如路径查找、迷宫求解、连通性分析等方面有着广泛的应用。深度优先搜索（DFS）是一种沿着图的边深入直到最后一个顶点，然后回溯并尝试另一条路径的算法。它使用递归或栈来实现，可以看作是树的先序遍历的推广。DFS的特点在于它尽可能深地搜索图的分支，当一条路走到尽头时，它会回溯到上一个顶点，然后继续搜索另一条路径。
  • 代码随想录算法训练营第五十七天 | 图论part07 sagen aller 算法图论
    53.寻宝prim算法prim算法#include#include#include#includeusingnamespacestd;intmain(){intv,e;intv1,v2,val;ifstreaminfile("input.txt");cin>>v>>e;vector>graph(v+1,vector(v+1,INT_MAX));while(e--){cin>>v1>>v2>>val
  • DAY60-图论-Bellman_ford No.Ada LeetCode刷题手册图论
    Bellman_ford队列优化算法（又名SPFA）publicstaticvoidmain(String[]args){Scannerscan=newScanner(System.in);intn=scan.nextInt();intm=scan.nextInt();//初始化List>edges=newArrayListtemp=newArrayListqueue=newLinkedListt
  • 代码随想录训练营 Day50打卡 图论part01 理论基础 98. 所有可达路径 那一抹阳光多灿烂 力扣图论图论深度优先算法
    代码随想录训练营Day50打卡图论part01一、理论基础DFS（深度优先搜索）和BFS（广度优先搜索）在图搜索中的核心区别主要体现在搜索策略上：1、搜索方向：DFS：深度优先，一条路走到黑。DFS从起点开始，选择一个方向深入到底，遇到死胡同再回溯，换一个方向继续探索。这种方式适合解决路径和组合问题，常与递归和回溯算法结合使用。BFS：广度优先，层层推进。BFS以起点为中心，一层层扩展，首先访问所
  • 每日刷题（图论） 何不遗憾呢 图论算法c++
    P1119灾后重建P1119灾后重建-洛谷|计算机科学教育新生态(luogu.com.cn)思路看数据范围知道需要用到Floyd算法，但是道路是不能直接用的，需要等到连接道路的两个村庄重建好才可以使用，所以这需要按照时间依次加入中转点，再更新dis数组。代码#include#defineintlonglong#defineTESTintT;cin>>T;while(T--)#defineiosio
  • 算法训练营|图论第4天 110.字符串接龙 105.有向图的完全可达性 106.岛屿的周长 人间温柔观察者 算法图论
    题目：110.字符串接龙题目链接：110.字符串接龙(kamacoder.com)代码：#include#include#includeusingnamespacestd;intmain(){intn;cin>>n;stringbeginStr,endStr;cin>>beginStr>>endStr;setMySet;for(inti=0;i>str;MySet.insert(str);}uno
  • 图论基础1 万事尽全力 算法题汇总图论算法
    图的储存方式邻接矩阵用二维数组来表示图结构。邻接矩阵是从节点的角度来表示图，有多少节点就申请多大的二维数组。在边少，节点多的情况下，会导致申请过大的二维数组，造成空间浪费。检查任意两个顶点间是否存在边的操作非常快适合稠密图，在边数接近顶点数平方的图中，邻接矩阵是一种空间效率较高的表示方法。邻接表用数组+链表的方式来表示。邻接表是从边的数量来表示图，有多少边才会申请对应大小的链表。对于稀疏图的存储，
  • 算法训练营|图论第8天 拓扑排序 dijkstra 人间温柔观察者 算法图论数据结构
    题目：拓扑排序题目链接：117.软件构建(kamacoder.com)代码：#include#includeusingnamespacestd;intmain(){intn,m;cin>>n>>m;vectorinDegree(n,0);unordered_map>myMap;vectorresult;for(inti=0;i>s>>t;inDegree[t]++;myMap[s].push_ba
  • 【图论简介】 WA-自动机 图论深度优先算法架构后端前端面试
    图论简介图论是一门数学分支，主要研究图（Graph）的性质、结构和应用。图论在计算机科学、网络理论、优化问题、生物信息学等多个领域都有广泛的应用。本文将简要介绍图论的基本概念、常见算法及其在实际中的应用。一、图的基本概念图（Graph）：图是由一组顶点（Vertices）和连接顶点的边（Edges）组成的结构。可以表示为(G=(V,E))，其中(V)是顶点的集合，(E)是边的集合。根据边的不同属性
  • 求任意两顶点间最短路算法及其matlab程序详解 夏天天天天天天天# 图论算法图论matlab
    #################本文为学习《图论算法及其MATLAB实现》的学习笔记#################算法用途图中任意两点间最短路的求法算法思想利用求最短路的Floyd算法的思想。首先,求得最短距离矩阵;然后,求任意给定两个顶点间的最短路所包含的顶点。程序参数说明W:图的权值矩阵k1:始点k2:终点P:k1，k2之间的最短路，顶点以经过次序排列u:最短路的距离算法的matlab程
  • [Python图论]在用图nx.shortest_path求解最短路径时，节点之间有多条边edge，会如何处理？ William数据分析 pythonpython信息可视化图论
    问：在使用图求最短路径时，如果节点之间有多条路径，shortest_route=nx.shortest_path(G,source=start_node,target=end_node,weight='length')会如何处理，会自动选择最短那条吗？#输出图G各节点之间有多少条边edge,并给出其长度Edgesbetween103928and25508583:共2条Edge:103928->25
  • 代码随想录算法训练营Final Day|| 感想总结篇+个人介绍和规划 傲世尊 算法
    也算是一期不落完完整整地追完了训练营的内容。虽然图论章节有点懈怠了，感觉每天都是理解后抄代码。。。前面所有章节都是每天做到能独立从头写到尾才算打卡（虽然最前面几道难题很可能又忘了）。这确确实实是很辛苦的两个月。因为目前还在毕业实习，每天朝九晚五的上班，还要准备实习报告，修改简历，准备秋招，期间还有几个学校的小项目要做。在加入训练营之前，我还是个每天下班就开始摸鱼躺平的“懒人”，直到内心的焦虑战胜了
  • 代码随想录打卡第五十八天 zengy5 代码随想录刷题流程算法c++leetcode开发语言
    代码随想录–图论部分day58图论第八天文章目录代码随想录--图论部分一、卡码网117--软件构建二、卡码网47--参加科学大会一、卡码网117–软件构建代码随想录题目链接：代码随想录某个大型软件项目的构建系统拥有N个文件，文件编号从0到N-1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件A依赖于文件B，则必须在处理文件A之前处理文件B（0#include#include#incl
  • 打卡第60天------图论 感谢上Di_123 前端算法题图论
    加油！尽管前面的道路很困难，但是依然要坚持下去✊。在算法训练营我学到了很多东西，对于算法的方法来说真的是涨知识了，对于我一个非科班出身，半路转行的干IT的人来说真的给予了我很大的帮助。我会继续回头看代码随想录分享的那些干货的，温故而知新。接下来我就要开始去攻克前端的框架源码和底层原理了，技术深度不够，面试总是挂，要攻克薄弱点了。今天大家会感受到Bellman_ford算法系列在不同场景下的应用。建
  • TOMCAT在POST方法提交参数丢失问题 357029540 javatomcatjsp
    摘自http://my.oschina.net/luckyi/blog/213209 昨天在解决一个BUG时发现一个奇怪的问题，一个AJAX提交数据在之前都是木有问题的，突然提交出错影响其他处理流程。 检查时发现页面处理数据较多，起初以为是提交顺序不正确修改后发现不是由此问题引起。于是删除掉一部分数据进行提交，较少数据能够提交成功。 恢复较多数据后跟踪提交FORM DATA ，发现数
  • 在MyEclipse中增加JSP模板 删除-2008-08-18 ljy325 jspxmlMyEclipse
    在D:\Program Files\MyEclipse 6.0\myeclipse\eclipse\plugins\com.genuitec.eclipse.wizards_6.0.1.zmyeclipse601200710\templates\jsp  目录下找到Jsp.vtl，复制一份，重命名为jsp2.vtl,然后把里面的内容修改为自己想要的格式，保存。 然后在 D:\Progr
  • JavaScript常用验证脚本总结 eksliang JavaScriptjavaScript表单验证
         转载请出自出处：http://eksliang.iteye.com/blog/2098985        下面这些验证脚本，是我在这几年开发中的总结，今天把他放出来，也算是一种分享吧，现在在我的项目中也在用！包括日期验证、比较，非空验证、身份证验证、数值验证、Email验证、电话验证等等...! &nb
  • 微软BI（4） 18289753290 微软BI SSIS
    1） Q:查看ssis里面某个控件输出的结果：  A MessageBox.Show(Dts.Variables["v_lastTimestamp"].Value.ToString()); 这是我们在包里面定义的变量 2):在关联目的端表的时候如果是一对多的关系，一定要选择唯一的那个键作为关联字段。 3) Q：ssis里面如果将多个数据源的数据插入目的端一
  • 定时对大数据量的表进行分表对数据备份 酷的飞上天空 大数据量
    工作中遇到数据库中一个表的数据量比较大，属于日志表。正常情况下是不会有查询操作的，但如果不进行分表数据太多，执行一条简单sql语句要等好几分钟。。   分表工具：linux的shell + mysql自身提供的管理命令 原理：使用一个和原表数据结构一样的表，替换原表。   linux shell内容如下： =======================开始 
  • 本质的描述与因材施教 永夜-极光 感想随笔
             不管碰到什么事,我都下意识的想去探索本质,找寻一个最形象的描述方式。        我坚信,世界上对一件事物的描述和解释,肯定有一种最形象,最贴近本质,最容易让人理解        &
  • 很迷茫。。。 随便小屋 随笔
    小弟我今年研一，也是从事的咱们现在最流行的专业（计算机）。本科三流学校，为了能有个更好的跳板，进入了考研大军，非常有幸能进入研究生的行业（具体学校就不说了，怕把学校的名誉给损了）。   先说一下自身的条件，本科专业软件工程。主要学习就是软件开发，几乎和计算机没有什么区别。因为学校本身三流，也就是让老师带着学生学点东西，然后让学生毕业就行了。对专业性的东西了解的非常浅。就那学的语言来说
  • 23种设计模式的意图和适用范围 aijuans 设计模式
    Factory Method 意图 定义一个用于创建对象的接口，让子类决定实例化哪一个类。Factory Method 使一个类的实例化延迟到其子类。 　　适用性 当一个类不知道它所必须创建的对象的类的时候。 　　当一个类希望由它的子类来指定它所创建的对象的时候。 　　当类将创建对象的职责委托给多个帮助子类中的某一个，并且你希望将哪一个帮助子类是代理者这一信息局部化的时候。 Abstr
  • Java中的synchronized和volatile aoyouzi javavolatilesynchronized
    说到Java的线程同步问题肯定要说到两个关键字synchronized和volatile。说到这两个关键字，又要说道JVM的内存模型。JVM里内存分为main memory和working memory。 Main memory是所有线程共享的，working memory则是线程的工作内存，它保存有部分main memory变量的拷贝，对这些变量的更新直接发生在working memo
  • js数组的操作和this关键字 百合不是茶 js数组操作this关键字
    js数组的操作;   一:数组的创建: 1、数组的创建 var array = new Array();　//创建一个数组 var array = new Array([size]);　//创建一个数组并指定长度，注意不是上限，是长度 var arrayObj = new Array([element0[, element1[, ...[, elementN]]]
  • 别人的阿里面试感悟 bijian1013 面试分享工作感悟阿里面试
    原文如下：http://greemranqq.iteye.com/blog/2007170         一直做企业系统，虽然也自己一直学习技术，但是感觉还是有所欠缺，准备花几个月的时间，把互联网的东西，以及一些基础更加的深入透析，结果这次比较意外，有点突然，下面分享一下感受吧！    &nb
  • 淘宝的测试框架Itest Bill_chen springmaven框架单元测试JUnit
    Itest测试框架是TaoBao测试部门开发的一套单元测试框架，以Junit4为核心， 集合DbUnit、Unitils等主流测试框架，应该算是比较好用的了。 近期项目中用了下，有关itest的具体使用如下： 1.在Maven中引入itest框架： <dependency>   <groupId>com.taobao.test</groupId&g
  • 【Java多线程二】多路条件解决生产者消费者问题 bit1129 java多线程
    package com.tom; import java.util.LinkedList; import java.util.Queue; import java.util.concurrent.ThreadLocalRandom; import java.util.concurrent.locks.Condition; import java.util.concurrent.loc
  • 汉字转拼音pinyin4j 白糖_ pinyin4j
    以前在项目中遇到汉字转拼音的情况，于是在网上找到了pinyin4j这个工具包，非常有用，别的不说了，直接下代码：   import java.util.HashSet; import java.util.Set; import net.sourceforge.pinyin4j.PinyinHelper; import net.sourceforge.pinyin
  • org.hibernate.TransactionException: JDBC begin failed解决方案 bozch ssh数据库异常DBCP
    org.hibernate.TransactionException: JDBC begin failed:     at org.hibernate.transaction.JDBCTransaction.begin(JDBCTransaction.java:68)    at org.hibernate.impl.SessionImp
  • java-并查集（Disjoint-set）-将多个集合合并成没有交集的集合 bylijinnan java
    import java.util.ArrayList; import java.util.Arrays; import java.util.HashMap; import java.util.HashSet; import java.util.Iterator; import java.util.List; import java.util.Map; import java.ut
  • Java PrintWriter打印乱码 chenbowen00 java
    一个小程序读写文件，发现PrintWriter输出后文件存在乱码，解决办法主要统一输入输出流编码格式。 读文件： BufferedReader 从字符输入流中读取文本，缓冲各个字符，从而提供字符、数组和行的高效读取。 可以指定缓冲区的大小，或者可使用默认的大小。大多数情况下，默认值就足够大了。 通常，Reader 所作的每个读取请求都会导致对基础字符或字节流进行相应的读取请求。因
  • [天气与气候]极端气候环境 comsci 环境
          如果空间环境出现异变...外星文明并未出现,而只是用某种气象武器对地球的气候系统进行攻击,并挑唆地球国家间的战争,经过一段时间的准备...最大限度的削弱地球文明的整体力量,然后再进行入侵......      那么地球上的国家应该做什么样的防备工作呢?  &n
  • oracle order by与union一起使用的用法 daizj UNIONoracleorder by
    当使用union操作时，排序语句必须放在最后面才正确，如下： 只能在union的最后一个子查询中使用order by，而这个order by是针对整个unioning后的结果集的。So： 如果unoin的几个子查询列名不同，如 Sql代码  select supplier_id, supplier_name  from suppliers  UNI
  • zeus持久层读写分离单元测试 deng520159 单元测试
    本文是zeus读写分离单元测试,距离分库分表,只有一步了.上代码: 1.ZeusMasterSlaveTest.java package com.dengliang.zeus.webdemo.test; import java.util.ArrayList; import java.util.List; import org.junit.Assert; import org.j
  • Yii 截取字符串(UTF-8) 使用组件 dcj3sjt126com yii
    1.将Helper.php放进protected\components文件夹下。 2.调用方法：   Helper::truncate_utf8_string($content,20,false);   //不显示省略号  Helper::truncate_utf8_string($content,20);  //显示省略号  &n
  • 安装memcache及php扩展 dcj3sjt126com PHP
    安装memcache    tar zxvf memcache-2.2.5.tgz     cd memcache-2.2.5/     /usr/local/php/bin/phpize (?)    ./configure --with-php-confi
  • JsonObject 处理日期 feifeilinlin521 javajsonJsonOjbectJsonArrayJSONException
        写这边文章的初衷就是遇到了json在转换日期格式出现了异常 net.sf.json.JSONException: java.lang.reflect.InvocationTargetException  原因是当你用Map接收数据库返回了java.sql.Date 日期的数据进行json转换出的问题话不多说  直接上代码  &n
  • Ehcache（06）——监听器 234390216 监听器listenerehcache
    监听器          Ehcache中监听器有两种，监听CacheManager的CacheManagerEventListener和监听Cache的CacheEventListener。在Ehcache中，Listener是通过对应的监听器工厂来生产和发生作用的。下面我们将来介绍一下这两种类型的监听器。  
  • activiti 自带设计器中chrome 34版本不能打开bug的解决 jackyrong Activiti
      在acitivti modeler中，如果是chrome 34，则不能打开该设计器，其他浏览器可以， 经证实为bug，参考 http://forums.activiti.org/content/activiti-modeler-doesnt-work-chrome-v34 修改为，找到 oryx.debug.js 在最头部增加 if (!Document.
  • 微信收货地址共享接口-终极解决 laotu5i0 微信开发
       最近要接入微信的收货地址共享接口，总是不成功，折腾了好几天，实在没办法网上搜到的帖子也是骂声一片。我把我碰到并解决问题的过程分享出来，希望能给微信的接口文档起到一个辅助作用，让后面进来的开发者能快速的接入，而不需要像我们一样苦逼的浪费好几天，甚至一周的青春。各种羞辱、谩骂的话就不说了，本人还算文明。    如果你能搜到本贴，说明你已经碰到了各种 ed
  • 关于人才 netkiller.github.com 工作面试招聘netkiller人才
    关于人才 每个月我都会接到许多猎头的电话，有些猎头比较专业，但绝大多数在我看来与猎头二字还是有很大差距的。 与猎头接触多了，自然也了解了他们的工作，包括操作手法，总体上国内的猎头行业还处在初级阶段。 总结就是“盲目推荐，以量取胜”。 目前现状 许多从事人力资源工作的人，根本不懂得怎么找人才。处在人才找不到企业，企业找不到人才的尴尬处境。 企业招聘，通常是需要用人的部门提出招聘条件，由人
  • 搭建 CentOS 6 服务器 - 目录 rensanning centos
    (1) 安装CentOS ISO（desktop/minimal）、Cloud（AWS/阿里云）、Virtualization（VMWare、VirtualBox） 详细内容 (2) Linux常用命令 cd、ls、rm、chmod...... 详细内容 (3) 初始环境设置 用户管理、网络设置、安全设置...... 详细内容 (4) 常驻服务Daemon
  • 【求助】mongoDB无法更新主键 toknowme mongodb
      Query query = new Query();          query.addCriteria(new Criteria("_id").is(o.getId()));                &n
  • jquery 页面滚动到底部自动加载插件集合 xp9802 jquery
    很多社交网站都使用无限滚动的翻页技术来提高用户体验，当你页面滑到列表底部时候无需点击就自动加载更多的内容。下面为你推荐 10 个 jQuery 的无限滚动的插件： 1. jQuery ScrollPagination jQuery ScrollPagination plugin 是一个 jQuery 实现的支持无限滚动加载数据的插件。 2. jQuery Screw S
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他