张量分解学习(一 基础铺垫)
在经过痛并快乐着的 张量基础学习之后 之后 ,我们终于可以在慢慢科研路之张量篇上再进一步了,好事多磨,万事都是开头难,不过前面的基础打好了,概念清晰了,后面自然就水道渠成了,废话不多说,上才艺!
Tensor decomposition
- 一 . 新征程,新方法
- 二 . 纤维和切片(Fiber and Slice)
- (1)纤维 —— Fiber
- (1)切片 —— Slice
- 三. 知识点串烧
- (1)范数
- (2)秩1 张量
- (3)立方 对角 超对称 对角张量
- 四. Matricization 矩阵化
一 . 新征程,新方法
前面,我们详细的为大家介绍过什么是张量,并用一张张简介而又不失内涵的图片帮助大家一步一步的理解,所以,我这里再用图片概括前面的表示法作其终点:
可爱吧,想笑吧,马上你就笑不出来了ヽ(ー_ー)ノ
矩阵一直都是我们学习新张量知识的突破口,这次也不例外,我们用下图来表示一个矩阵,其想法来源于:一个带有实数项的 m × n m\times n m×n 矩阵 可以表示 R n \mathbb{R}^{n} Rn 到 R m \mathbb{R}^{m} Rm的线性映射,左边的线代表输入通道,右边的线必然就是输出的通道了,中间的圆圈可能就是某种变换作用,说道这里,我突然有想到我们在量子计算专栏中的 各种算子算符 不就是这个道理吗??机智如我~~
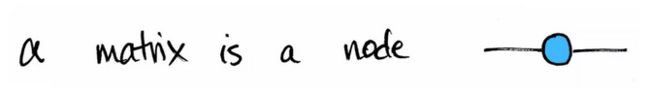
还可以再进一步,算子的左乘右乘也是影响输出来矢量或者矩阵维数的重要因素,所以,我们按照上图的思路再完善一下:
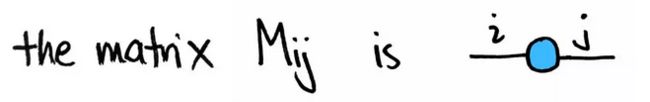 索引 i 的范围从 1 到 m,表示输出空间的维数;j 的范围从 1 到 n,表示输入空间的维数。换言之,i 表示 M 的行数,j 表示其列数。
索引 i 的范围从 1 到 m,表示输出空间的维数;j 的范围从 1 到 n,表示输入空间的维数。换言之,i 表示 M 的行数,j 表示其列数。
好,那么根据矩阵的新表示方法,我们也可以尝试将其他维数的张量画出来,这个圆圈表示的是某种确定的线性映射关系,不能动,那么要表示维数的不同也就只能在“线” 上做文章了:

之所以介绍这种方法,不仅方便了后面张量分解的学习,也为张量网络的构建埋下了伏笔!具体的应用我们日后再叙~~
二 . 纤维和切片(Fiber and Slice)
在张量分解学习之前,我们先要看一看对于高维张量,是否存在一些手段规则能降维处理,或者是简单展开,因为张量分解也必定有着属于自己的一套展开方法,这是需要我们摸索前进的过程!
在这之前,启用以下常规字体设定:小写加粗字母例如 x \boldsymbol{x} x 代表向量,大写加粗字母 X \boldsymbol{X} X代表矩阵,花体 X \mathcal{X} X 代表张量!
(1)纤维 —— Fiber
纤维是指从张量中抽取向量的操作。在矩阵中固定其中一个维度,可以得到行或列。类似于矩阵操作,固定其它维度,只保留一个维度变化,可以得到纤维的概念。
当我们将一个张量沿着他的第k个维展开的时候,我们就获得了mode-k fiber ,例如,三阶张量 X \mathcal{X} X 的 mode-1 fiber 为 x : j k \boldsymbol{x_{:jk}} x:jk (注意此时表示的指标已经变成向量了),因此其有三种纤维化的方法,如下图:
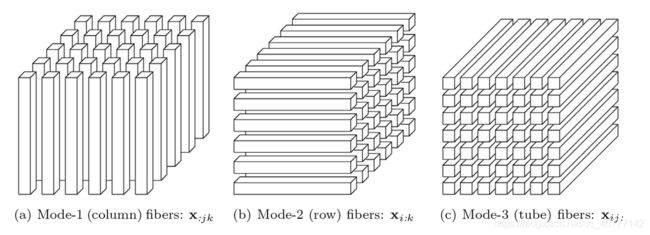
其实我的理解非常的简单,我们把张量想象成一个一个形状比较规则的土豆,那么纤维就是 给他切成土豆丝儿,根据您的心情和喜好,可以采用不同方向的切法,一个是“站着”,一个是“横着”,一个是“躺着”,进而得到不同的“纤维”。
(1)切片 —— Slice
土豆既然能切成丝儿,我也就能切成片儿,不过我们得到的就不是矢量了,而是矩阵。
切片是指在张量中抽取矩阵的操作。在张量中如果保留两个维度变化,其它的维度变化可以得到一个矩阵,这个矩阵即为张量的切片当我们除了2个维度展开以外维持所有index不变时,我们就获得了slice.
例如,三阶张量 X \mathcal{X} X 的horizontal slice为: X i : : X_{i::} Xi::,同样也是有三种切法:

三. 知识点串烧
在正式进入分解之前,我们为了后面不会一脸懵,所以必要的铺垫还是要有的,这里我们一一介绍几个重要的知识点:
(1)范数
范数,是具有 “长度” 概念的函数。在线性代数、泛函分析及相关的数学领域,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小,范数有多种,L1,L2,Lp等等,在这里并不需要展开讲,你只需要了解下面这个:
张量norm的定义和矩阵范数的定义类似,均为所有元素的平方之和开根,对于张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN来说,其范数为:
∥ X ∥ = ∑ i 1 = 1 I 1 ∑ i 2 = 1 I 2 ⋯ ∑ i N = 1 I N x i 1 i 2 ⋯ N 2 \|\mathcal{X}\|=\sqrt{\sum_{i 1=1}^{I_{1}} \sum_{i 2=1}^{I_{2}} \cdots \sum_{i N=1}^{I_{N}} x_{i_{1} i_{2} \cdots N}^{2} } ∥X∥=i1=1∑I1i2=1∑I2⋯iN=1∑INxi1i2⋯N2
求都嘛得!是否,你还记得内积的定义?是否,你还记得阶数相同张量的内积?是否,你还记得我…嗯嗯 ,不好意思,差点差点唱了起来。。。。
如果两个相等的矩阵进行内积,那么不就和上面的范数结果一样了吗,这肯定不是巧合!借此,我们目前可以大致得到下面这个式子:
⟨ X , X ⟩ = ∥ X ∥ 2 \langle\mathcal{X}, \mathcal{X}\rangle=\|X\|^{2} ⟨X,X⟩=∥X∥2
(2)秩1 张量
大家在线代里都会算矩阵的秩,但是张量学到现在,我们也没有详细的介绍过张量的秩是怎么回事,原因在于其的不确定和高难度,不过万丈高楼平地起,秩为一的张量我们还是要知道的,它比较特别,可以被向量(vector)的外积(outer product)所定义:
对于一个N阶张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN,当可以被写成N个向量的外积时,此张量的秩为1:
X = a 1 × a 2 × ⋯ × a n \mathcal{X} = \boldsymbol{a_{1}} \times \boldsymbol{a_{2}} \times \cdots \times \boldsymbol{a_{n}} X=a1×a2×⋯×an
目前只需记住它!
(3)立方 对角 超对称 对角张量
如果某个张量的所有维度都是相同的,我们将其称为:立方 。
之前的博客我们还介绍过张量的对称,但是它对对称性的要求并不高,这里我们要了解一下 :超对称( S u p e r s y m m e t r i c Supersymmetric Supersymmetric) ,其实就是立方张量在对称!
举个例子:对于3阶张量 X ∈ R I × I × I \mathcal{X} \in \mathbb{R}^{I\times I\times I} X∈RI×I×I ,如果满足下式,则是超对称的:
x i j k = x i k j = x j i k = x j k i = x k i j = x k j i for all i , j , k = 1 , 2 … I x_{i j k}=x_{i k j}=x_{j i k}=x_{j k i}=x_{k i j}=x_{k j i} \quad \text { for all } i, j, k=1, 2\ldots I xijk=xikj=xjik=xjki=xkij=xkji for all i,j,k=1,2…I
结合切片:张量在某些mode下符合对称的条件, 这时候我们只叫他在对应的mode下对称!
我们都知道对角矩阵,那么什么是对角张量?
定义:如果一个张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN 的任何元素只有在 i 1 = i 2 = ⋯ i N i_{1} = i_{2} = \cdots i_{N} i1=i2=⋯iN 的时候不为 0,也就是 x i 1 i 2 … i N ≠ 0 x_{i_{1} i_{2} \ldots i_{N}} \neq 0 xi1i2…iN=0 时,被称之对角张量。
- 如果对角张量同时是立方的,则只有超对角线(superdiagonal)所经过的元素不为0
- 对角张量对任何维度比例的张量其实都成立。
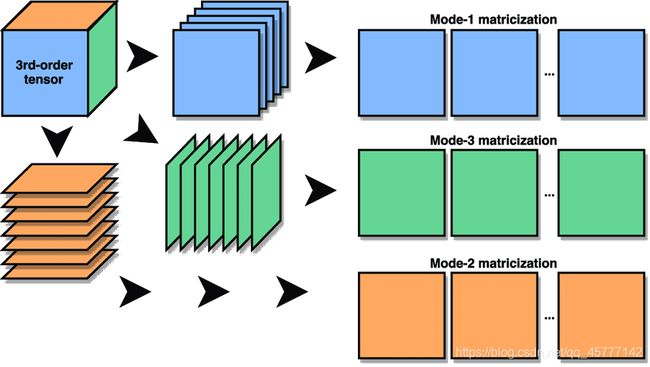
四. Matricization 矩阵化
矩阵化讲述了如何将高维张量拆解成2阶的矩阵。这是个极为重要的概念,日后将频繁出现在各种公式与定理之中,所以非常重要,其文字化定义意外的简单,而数学定义较为繁琐。
先看个小小的例子帮助理解,某张量如下图:
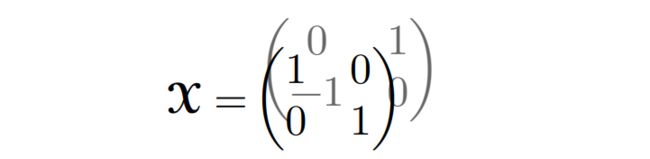
矩阵化之后就是这样:

有的小伙伴可能还是没看出来这里的规律哦,我从我老师那里搞来了三张图,保你瞬间名茅塞顿开:
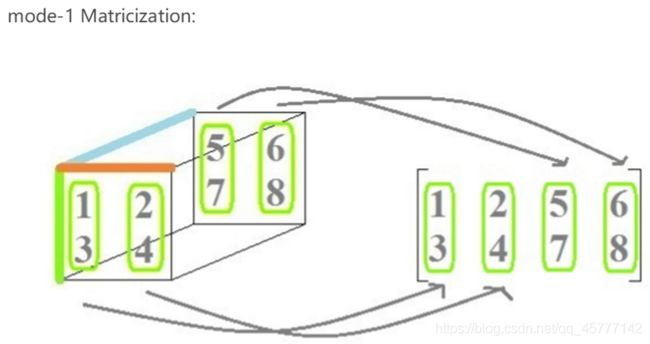
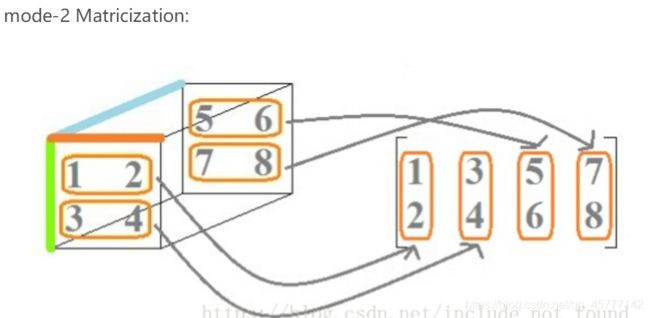
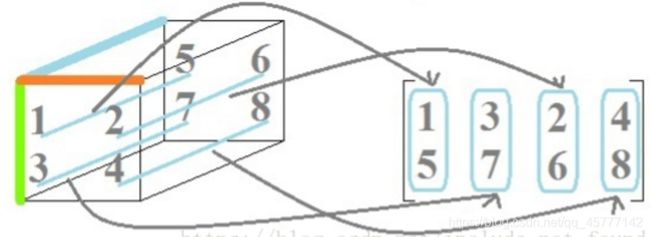
这就相当于张量切片,切片有几种,这就有几种,只是将得到的切片平铺在纸面上!
还有一个点需要提醒大家,看第三个图,图中不是先排1-5这个一条嘛,接着就按列取了 3-7这一条,可是理论上紧接着可以取2-6这一条,所以,在model-3 中的矩阵化中有两种方法,下次遇到有个印象就行!
- 文字化定义:对于张量 X ∈ R I 1 × I 2 × ⋯ × I N \mathcal{X} \in \mathbb{R}^{I_{1} \times I_{2} \times \cdots \times I_{N}} X∈RI1×I2×⋯×IN 来说,我们称其mode-n的矩阵化为 X ( n ) \boldsymbol{X_{(n)}} X(n) ,通过把 X \mathcal{X} X 的每一根mode-n fiber按序插入这个矩阵的列中,我们就完成了矩阵化。
- 数学定义必须定义其顺序,所以稍显复杂,我们定义一个从张量元素 ( i 1 , i 2 , ⋯ i n ) (i_{1},i_{2},\cdots i_{n}) (i1,i2,⋯in) 到矩阵元素 ( i n , j ) (i_{n},j) (in,j)的映射:
j = 1 + ∑ k = 1 k ≠ n N ( i k − 1 ) J k with J k = ∏ m = 1 m ≠ n j − 1 I m j=1+\sum_{k=1 \atop k \neq n}^{N}\left(i_{k}-1\right) J_{k} \quad \text { with } \quad J_{k}=\prod_{m=1 \atop m \neq n}^{j-1} I_{m} j=1+k=nk=1∑N(ik−1)Jk with Jk=m=nm=1∏j−1Im
其实这个纯数学定义法不用管,只因放上去会显得我的博客 m o r e more more p r o f e s s i o n a l professional professional …ψ(*`ー´)ψ
说了在我个人看来,图最好懂:
假设某张量 X ∈ R 3 × 4 × 2 \mathcal{X} \in \mathbb{R}^{3\times 4\times 2} X∈R3×4×2的 frontal slices如下 :
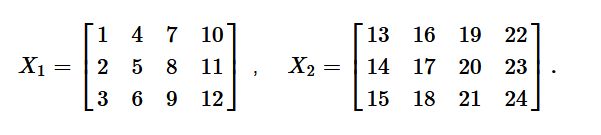
矩阵化之后: