一. 原理:
动态规划:
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的。
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到
这个性质叫做最优子结构;
而
不管之前这个状态是如何得到的
这个性质叫做无后效性。
什么是动态规划?动态规划的意义是什么?
二. 举个:
假设你是一个小偷,背着一个可装4磅东西的背包,你可盗窃的商品有如下3件。
为了让盗窃的商品价值最高,你该如何选择商品。
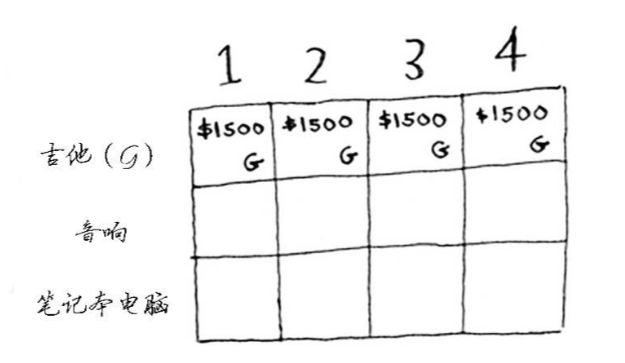
1. 背包问题的网格如下:
网格的各行为商品,各列为不同容量(1-4磅)的背包,所有的这些列你都需要,因为它将帮助你计算子背包的价值。
2. 吉他行
意味着你尝试将吉他装入背包。在每个单元格,都需要做简单的决定:偷不偷吉他?然后找出价值最高的商品集合。第一个单元格表示背包的重量为1磅,吉他重量也是1磅,所以能装入背包。以此类推。吉他行单元格如下所示:
3. 音响行
音响行处于第二行,表示现在可偷的商品有吉他和音响。在每一行,可偷的商品都为当前行的商品以及之前各行的商品。
我们先来看第一个单元格,他表示容量为1磅的背包,在此之前,可装入1磅背包的商品的最大价值是1500美元。因为音响重4磅,所以第一个单元格没法装音响,只能装吉他。
以此类推,当背包容量为2磅和3磅时,也只能装吉他,偷不来音响。
当背包容量为4磅时,能装入音响,因为音响价值3000美元,高于吉他的1500美元,所以为了价值最高,当然是偷音响。
音响行单元格如下所示:
4. 笔记本电脑行
以同样的方式处理笔记本电脑,因为笔记本电脑重达到3磅,没法装入容量为1磅或2磅的背包,因此:前两个单元格的最大价值还是1500美元。
但对于容量为3磅的背包,原来最大价值为1500美元,但现在你可以选择盗窃价值为2000美元的笔记本电脑而不是吉他,这样第三个单元格最大价值为2000美元。
对于容量为4磅的背包,当前最大的价值为3000美元,但是你可以选择不偷音响,而偷笔记本电脑和吉他,笔记本电脑2000美元,吉他1500美元,总价值3500美元。
笔记本电脑行单元格如下:
所以将吉他和笔记本电脑装入背包时价值最高,为3500美元。
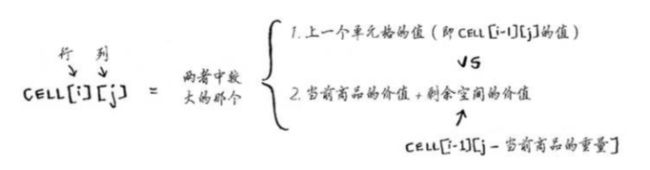
从上面单元格的图中可以看出:在计算每个单元格的价值时,使用的公式都相同,公式如下:
5. 代码展示:
typedef struct StructGood {
// 商品 重量
int goodWeight;
// 商品 价值
int goodValue;
} Good;
int main(int argc, const char * argv[]) {
// 背包 最大 磅数
int maxCapacity = 4;
// 吉他
Good guitarGood = {1, 1500};
// 音响
Good soundGood = {4, 3000};
// 笔记本 电脑
Good computerGood = {3, 2000};
// 商品 数组
Good goodArray[3] = {guitarGood, soundGood, computerGood};
// 单元格 数组
int tableCellArray[3][4] = {0};
// 商品
for (int i = 0; i < 3; i++) {
// 背包 容量
for (int j = 0; j < maxCapacity; j++) {
// 当前商品
Good tmpGood = goodArray[i];
// 真正 背包容量
int realCapacity = j + 1;
// 当多余1个商品
if (i > 0) {
// 如果 背包 容量 大于 商品 重量
if (realCapacity > tmpGood.goodWeight) {
int tmpMaxGoodValue = tmpGood.goodValue + tableCellArray[i - 1][realCapacity - tmpGood.goodWeight];
if (tmpMaxGoodValue < tableCellArray[i - 1][j]) {
tmpMaxGoodValue = tableCellArray[i - 1][j];
}
tableCellArray[i][j] = tmpMaxGoodValue;
}
// 如果 背包 容量 等于 商品 重量
else if(realCapacity == tmpGood.goodWeight){
int tmpMaxGoodValue = tmpGood.goodValue;
if (tmpMaxGoodValue < tableCellArray[i - 1][j]) {
tmpMaxGoodValue = tableCellArray[i - 1][j];
}
tableCellArray[i][j] = tmpGood.goodValue;
}
// 如果 背包 容量 小于 商品 重量
else {
tableCellArray[i][j] = tableCellArray[i - 1][j];
}
}
// 当 只有 一个 商品
else {
if (tmpGood.goodWeight <= realCapacity) {
tableCellArray[i][j] = tmpGood.goodValue;
}
}
}
}
// 商品
for (int i = 0; i < 3; i++) {
// 背包 容量
for (int j = 0; j < maxCapacity; j++) {
printf("%d ", tableCellArray[i][j]);
}
printf("\n");
}
return 0;
}
三. 常见使用:
1. 斐波那契数列
详见:漫画:什么是动态规划?(整合版)
有一座
高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。
A. 问题建模:
假设你只差最后一步就走到第10级台阶,因为每一步只能走1级或者2级这时候会出现两种情况:
第一种是从9级直接走到10级第二种是从8级走到10级
也就是说要想走到第10级,最后一步必然是从8级或者9级开始。
那如果:我们已经知道从0级走到9级的走法有X种,从0级到8级的走法有Y种,为了方便表达我们把10级台阶走法的数量写为F(10),那么0级到10级的走法就是F(10) = X + Y = F(9) + F(8)。
因此很容易递推出,F(9) = F(8) + F(7), F(8) = F(7) + F(6)。
再考虑下如果只有1级台阶和2级台阶的时候,很显然1级台阶只有1种走法,2级台阶有2种走法。F(1) = 1; F(2) = 2;
所以我们可以归纳出如下的公式:
F(1) = 1;
F(2) = 2;
F(n) = F(n - 1) + F(n - 2) (n >= 3);
动态规划中包含三个重要的概念:
- 最优子结构
- 边界
- 状态转移公式
刚才我们分析出的:F(10) = F(9) + F(8),因此F(9)和F(8)是F(10)的最优子结构。
当只有1级台阶或2级台阶的时候,我们可以得出结果,无需转换,因此我们称F(1) 和F(2) 是问题的边界。如果一个问题没有边界就永远无法得到有限的结果。
而F(n) = F(n - 1) + F(n - 2) (n >= 3);是阶段与阶段之间的状态转移方程。这是动态规划的核心,决定了问题的每一个阶段和下一个阶段的关系。
这是我们完成了: 问题建模,接下来我们进行:求解问题。
B. 求解问题
a. 解法1:递归求解
首先很容易想到递归求解:
接下来我们分析下递归求解的时间复杂度:
要计算出F(N), 就要得到F(N - 1) 和 F(N - 2)的值,要计算F(N - 1),就得计算出F(N - 2)和 F(N - 3)的值,以此类推,可以归纳出下图:
不难看出,这是一个二叉树,高度为N - 1, 节点个数接近2的N-1次方。所以方法的时间复杂度可以近似看做O(2^N);
显然时间复杂度是指数级别,这是不可接受的。
b. 解法二:备忘录算法
从二叉树图中可以很明显的看出,很多相同的参数被重复计算了,所以很容易想到将需要重复计算的值,用哈希表先进行存储,当遇到相同参数时,再直接从哈希表取出,就不用重复计算。这种暂时存储计算结果的方式叫做备忘录算法。
以上代码中集合map是一个备忘录。当每次需要计算F(N)的时候,会首先从map中寻找匹配元素。如果map中存在,就直接返回结果,如果map中不存在,就计算出结果,存入备忘录中。
从中我们不难分析出,从F(1)到 F(N)一共有N个不同的输入,在哈希表中存储了N-2个结果,所以时间复杂度和空间复杂度都是O(N);
c. 解法三: 动态规划求解
备忘录算法中,我们用到哈希表来存储重复计算的值,这样空间复杂度从O(1)扩大到O(N);有没有更好的方法,时间复杂度还是O(N),空间复杂度依然为O(1)的。
我们上面两种解法都是采用自顶向下来求解的,换个思路,采用自底向上来推导试试。
我们知道F(1) = 1; F(2) = 2; F(N) = F(N - 1) + F(N - 2) (n >= 3);
所以我们很容易求出F(3) = F(1) + F(2) = 1 + 2 = 3;这里F(3)只依赖于F(1)和F(2);
同样的F(4) = F(3) + F(2) = 3 + 2 = 5;这里F(4)只依赖于F(3)和F(2);
由此可见,每一次迭代过程中,只要保留之前的两个状态,就可以推导出新的状态,而不需要保留全部的子状态。
新的状态只与之前的两个状态有关,跟最开始的其他状态无关,这也是动态规划的无后效性的体现。
程序从i=3开始迭代,一直到i=n结束。每一次迭代,都会计算出多一级台阶的走法数量。迭代过程中只需保留两个临时变量a和b,分别代表了上一次和上上次迭代的结果。 为了便于理解,我引入了temp变量。temp代表了当前迭代的结果值。
从结果可以看出,采用自底向上的递推方式,实现了时间O(N)和空间O(1)的最优化。这就是动态归划。
再回过头去看背包问题,我们会发现背包问题的:
-
最优子结构:
边界:
当只有一件商品时,商品磅数如果大于等于背包磅数,就是当前商品的价值,否则为0;-
状态转移方程:
2. 最长公共子串
假如你做一款翻译器,当用户拼错单词时,你必须猜测他原来要输入的单词,例如,Alex想查单词fish,但不小心输入了hish.这时你需要找出最类似的单词,呈现给用户,这时你查找发现fish和vista这两个单词类似,你需要比较,找到最类似的单词,呈现给用户并翻译。
a. 绘制网格
单元格中的值是什么?
在这个问题里,要找出两个单词的最长公共子串。hish和fish都包含的最长子串是什么?有多少个?hish和vista都包含的最长子串是什么?有多少个?通过比较两者之间最长子串的总个数,来判别出,fish和vista两者和输入的hish的类似程度。
所以单元格的值就是两个字符串都包含的最长子串长度。
- 如何将
这个问题划分为子问题?
你可以需要比较子串:不是比较hish和fish,而是先比较his和fis。每个单元格都将包含这两个子串的最长公共子串的长度。
网格的坐标轴是什么?
因为单元格包含着这两个子串的最长公共子串的长度,所以坐标轴,应该分别为输入的字符串和类似的子串。
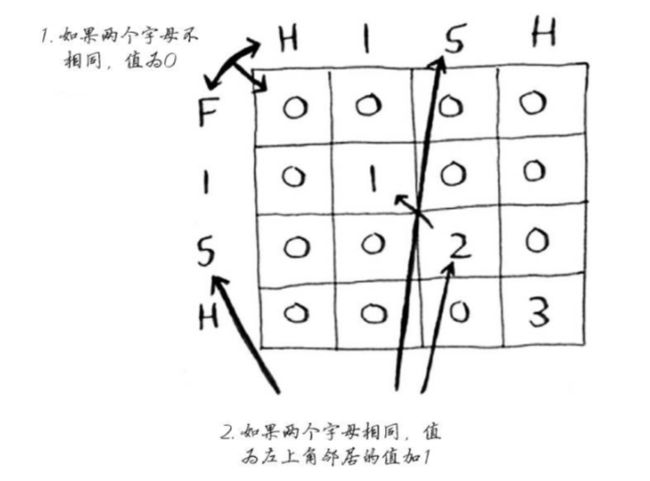
最终hish和fish的网格填充如下:
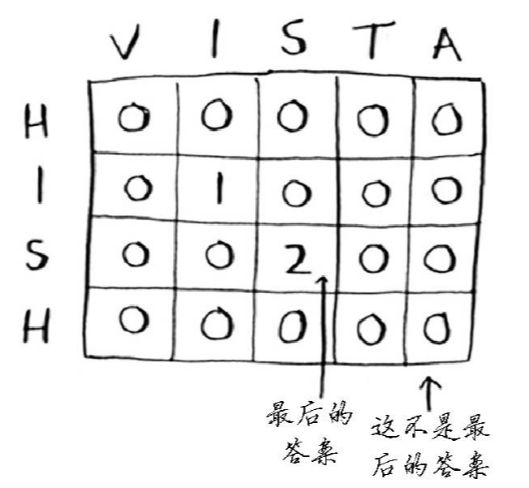
hish和vista的网格填充如下:
从上面单元格的值,可以总结出状态转移方程为:
实现代码:
// 最长 重复 子串
int maxSubStringLength(char *fristStr, int fristStrLength, char *secondStr, int secondStrLength) {
if (fristStr == NULL || secondStr == NULL) {
return 0;
}
if (fristStrLength == 0 || secondStrLength == 0) {
return 0;
}
int maxSubStrLength = 0;
// 开辟 存储 网格
int **postionArray = (int **)malloc(sizeof(int *) * (fristStrLength + 1));
for (int i = 0; i <= fristStrLength; i ++) {
postionArray[i] = (int *)malloc(sizeof(int) * (secondStrLength + 1));
}
// 初始化 存储 网格
for (int i = 0; i <= fristStrLength; i++) {
for (int j = 0; j <= secondStrLength; j++) {
postionArray[i][j] = 0;
}
}
// 遍历 网格
for (int i = 0; i < fristStrLength; i++) {
for (int j = 0; j < secondStrLength; j++) {
if (i == 0 || j == 0) {
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = 1;
}
else {
postionArray[i][j] = 0;
}
}
else {
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
if (maxSubStrLength < postionArray[i][j]) {
maxSubStrLength = postionArray[i][j];
}
}
else {
postionArray[i][j] = 0;
}
}
}
}
return maxSubStrLength;
}
int main(int argc, const char * argv[]) {
char firstStr[4] = {'h','i','s','h'};
char secondStr[4] = {'f','i','s','h'};
char threeStr[5] = {'v','i','s','t','a'};
int firstMax = maxSubStringLength(firstStr, 4, secondStr, 4);
int secondMax = maxSubStringLength(firstStr, 4, threeStr, 5);
if (firstMax > secondMax) {
printf("hish 和 fish最类似, 最长公共子串长度为:%d\n", firstMax);
}
else {
printf("hish 和 vista 最类似, 最长公共子串长度为:%d\n", secondMax);
}
return 0;
}
综上所述:
- 最优子结构:
当i > 0 && j > 0,
如果两个字符相同:postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
如果两个字符不同:postionArray[i][j] = 0;
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
}
else {
postionArray[i][j] = 0;
}
- 边界:
当i== 0或者j == 0
if (i == 0 || j == 0) {
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = 1;
}
else {
postionArray[i][j] = 0;
}
}
- 状态转移方程:
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
}
else {
postionArray[i][j] = 0;
}
3.最长公共子序列
假设Alex不小心输入了fosh,那他原本想输入的是fish还是fort。
因为fosh和fish有2个最长公共子串sh;fosh和fort也有2个最长公共子串fo。
所以这里应该比较最长公共子序列:两个单词中都有的序列包含的字母数。
所以这里单元格的值应该为当前子序列中包含的相同字母的个数。
最终网格如下:
填写网格所用公式:
实现代码如下:
// 最长 重复 子序列
int maxSubSequenceLength(char *fristStr, int fristStrLength, char *secondStr, int secondStrLength) {
if (fristStr == NULL || secondStr == NULL) {
return 0;
}
if (fristStrLength == 0 || secondStrLength == 0) {
return 0;
}
int maxSubStrLength = 0;
// 开辟 存储 网格
int **postionArray = (int **)malloc(sizeof(int *) * (fristStrLength + 1));
for (int i = 0; i <= fristStrLength; i ++) {
postionArray[i] = (int *)malloc(sizeof(int) * (secondStrLength + 1));
}
// 初始化 存储 网格
for (int i = 0; i <= fristStrLength; i++) {
for (int j = 0; j <= secondStrLength; j++) {
postionArray[i][j] = 0;
}
}
// 遍历 网格
for (int i = 0; i < fristStrLength; i++) {
for (int j = 0; j < secondStrLength; j++) {
if (i == 0 || j == 0) {
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = 1;
}
else {
if (i == 0 && j > 0) {
postionArray[i][j] = postionArray[i][j - 1];
}
else if(j == 0 && i > 0){
postionArray[i][j] = postionArray[i - 1][j];
}
else {
postionArray[i][j] = 0;
}
}
}
else {
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
if (maxSubStrLength < postionArray[i][j]) {
maxSubStrLength = postionArray[i][j];
}
}
else {
postionArray[i][j] = postionArray[i - 1][j] > postionArray[i][j - 1] ? postionArray[i - 1][j] : postionArray[i][j - 1];
}
}
}
}
return maxSubStrLength;
}
int main(int argc, const char * argv[]) {
char firstStr[4] = {'f','o','s','h'};
char secondStr[4] = {'f','i','s','h'};
char threeStr[4] = {'f','o','r','t'};
int firstMax = maxSubSequenceLength(firstStr, 4, secondStr, 4);
int secondMax = maxSubSequenceLength(firstStr, 4, threeStr, 5);
if (firstMax > secondMax) {
printf("fosh 和 fish最类似, 最长公共子串长度为:%d\n", firstMax);
}
else {
printf("fosh 和 fort 最类似, 最长公共子串长度为:%d\n", secondMax);
}
return 0;
}
综上所述:
- 最优子结构:
当i > 0 && j > 0,
如果两个字符相同:postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
如果两个字符不同:postionArray[i][j] = postionArray[i - 1][j] > postionArray[i][j - 1] ? postionArray[i - 1][j] : postionArray[i][j - 1];
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
}
else {
postionArray[i][j] = postionArray[i - 1][j] > postionArray[i][j - 1] ? postionArray[i - 1][j] : postionArray[i][j - 1];
}
- 边界:
当i== 0或者j == 0
if (i == 0 || j == 0) {
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = 1;
}
else {
if (i == 0 && j > 0) {
postionArray[i][j] = postionArray[i][j - 1];
}
else if(j == 0 && i > 0){
postionArray[i][j] = postionArray[i - 1][j];
}
else {
postionArray[i][j] = 0;
}
}
}
- 状态转移方程:
// 如果 两个 字符 相同
if (fristStr[i] == secondStr[j]) {
postionArray[i][j] = postionArray[i - 1][j - 1] + 1;
}
else {
postionArray[i][j] = postionArray[i - 1][j] > postionArray[i][j - 1] ? postionArray[i - 1][j] : postionArray[i][j - 1];
}