Leetcode题解-算法-搜索（python版）

1、BFS

1.1 将一个数分解为整数的平方和

279. 完全平方数(Medium)
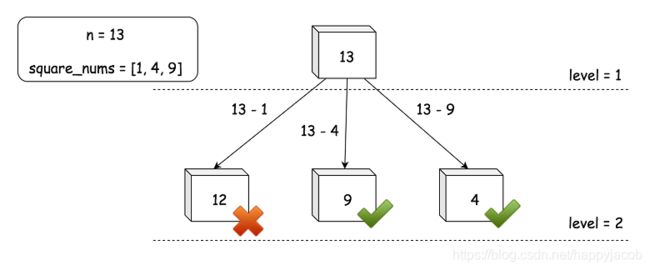
给定一个 N 元树，其中每个节点表示数字 n 的余数减去一个完全平方数的组合，我们的任务是在树中找到一个节点，该节点满足两个条件：

1. 节点的值（即余数）也是一个完全平方数
2. 节点和根之间的距离应该最小
   

• 首先，我们准备小于给定数字 n 的完全平方数列表（即 square_nums）
• queue 保存所有剩余项在每个级别的枚举
• 每次迭代，检查余数是否是一个完全平方数，是完全平方的余数就找到了答案，如果余数不是一个完全平方数，就用其中一个完全平方数减去它，得到一个新余数，然后将新余数添加到 next_queue 中，以进行下一级的迭代

注意：在典型的 BFS 算法中，queue 通常是列表类型。这里使用 set 类型，以消除同一级别中的剩余项的冗余。

class Solution:
    def numSquares(self, n: int) -> int:
        square_nums = [i * i for i in range(1, int(n ** 0.5) + 1)]
        queue = {n}
        step = 0
        while queue:
            step += 1
            next_queue = set()
            for remainder in queue:
                for squ_num in square_nums:
                    if squ_num == remainder:
                        return step
                    elif squ_num > remainder:
                        break
                    else:
                        next_queue.add(remainder - squ_num)
            queue = next_queue
        return step

1.2 最短单词路径

127. 单词接龙(Medium)

算法中最重要的步骤是找出相邻的节点，也就是只差一个字母的两个单词。为了快速的找到这些相邻节点，我们对给定的 wordList 做一个预处理，将单词中的某个字母用 * 代替。

对于每个单词遍历查看是否只差一个字母将花费很多时间。这步预处理找出了单词表中所有单词改变某个字母后的通用状态，可以更快的找到相邻节点。

利用广度优先搜索搜索从 beginWord 到 endWord 的路径。

1. 对给定的 wordList 做预处理，找出所有的通用状态。将通用状态记录在字典中，键是通用状态，值是对应的单词，例如 ‘*ot’: [‘hot’, ‘dot’, ‘lot’]， ‘h*t’: [‘hot’], ‘ho*’: [‘hot’]
2. 将包含 beginWord 和 1 的元组放入队列中，1 代表节点的层次
3. 为了防止出现环，使用访问数组记录，beginWord : True 表示 beginWord 已经访问过了
4. 当队列中有元素的时候，取出第一个元素，记为 current_word
5. 找到 current_word 的所有通用状态，并找出这些通用状态的单词映射，直接在字典 all_comb_dict 中查询
6. 从 all_combo_dict 获得的所有单词，和 current_word 都只差一个字母相连，如果就是目标单词直接返回 step + 1 即可，
7. 如果不是目标单词，继续查找，前面没有访问过，向队列中加入元素 (word, step + 1) 其中 step 是 current_word 的层次，并将访问状态设为 True

class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        if endWord not in wordList or not beginWord or not endWord or not wordList:
            return 0
        word_len = len(beginWord)
        all_comb_dict = defaultdict(list)
        for word in wordList:
            for i in range(word_len):
                all_comb_dict[word[:i] + "*" + word[i+1:]].append(word)
        queue = [(beginWord, 1)]
        visited = {beginWord : True}
        while queue:
            cur_word, step = queue.pop(0)
            for i in range(word_len):
                intermediate_word = cur_word[:i] + "*" + cur_word[i+1:]
                for word in all_comb_dict[intermediate_word]:
                    if word == endWord:
                        return step + 1
                    if word not in visited:
                        visited[word] = True
                        queue.append((word, step + 1))
                all_comb_dict[intermediate_word] = []
        return 0

1.3 K 站中转内最便宜的航班

bfs，广度优先搜索，先处理数据，以出发点为 key，到达站和价格为 value 构建字典，对处理好的数据进行 bfs。队列中保存的数据是站的位置，中转次数，从出发点到达此站的价格。

class Solution:
    def findCheapestPrice(self, n, flights, src, dst, K):
        from collections import defaultdict, deque
        flights_dict = defaultdict(list)
        for flight in flights:
            flights_dict[flight[0]].append((flight[1], flight[2]))
        queue = deque()
        queue.appendleft((src, 0, 0))
        min_cost = float("inf")
        while queue:
            start, counter, cur_cost = queue.pop()
            for end, price in flights_dict[start]:
                if end == dst and counter <= K:
                    min_cost = min(min_cost, cur_cost + price)
                if counter <= K and cur_cost + price <= min_cost:
                    queue.appendleft((end, counter+1, cur_cost + price))
        return min_cost if min_cost != float("inf") else -1

1.4 课程表

207. 课程表(Medium)

如果一个节点没有入边，就是没有任何的先修课程要求。当我们将一个节点加入答案中后，我们就可以移除它的所有出边，代表着它的相邻节点少了一门先修课程的要求。如果某个相邻节点变成了「没有任何入边的节点」，那么就代表着这门课可以开始学习了。按照这样的流程，我们不断地将没有入边的节点加入答案，直到答案中包含所有的节点或者图中包含环。

我们使用一个队列来进行广度优先搜索。

• 初始时，所有入度为 0 的节点都被放入队列中
• 取出队首的节点 cur_course，移除 cur_course 的所有出边，也就是将 cur_course 的所有相邻节点的入度减少 1。如果某个相邻节点的入度变为 0，就放入队列中。

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        edges = collections.defaultdict(list)
        enter_num = [0] * numCourses
        for info in prerequisites:
            edges[info[1]].append(info[0])
            enter_num[info[0]] += 1
        q = collections.deque([u for u in range(numCourses) if enter_num[u] == 0])
        have_learn = 0
        while q:
            have_learn += 1
            cur_course = q.popleft()
            for next_course in edges[cur_course]:
                enter_num[next_course] -= 1
                if enter_num[next_course] == 0:
                    q.append(next_course)
        return have_learn == numCourses

2、DFS

2.1 查找最大的连通面积

695. 岛屿的最大面积(Medium)

深度优先搜索，求网格中每个连通形状的面积，然后取最大值。

• 对于存在陆地的地方，向 4 个方向探索与之相连的每一个土地，经过的土地总数将是该连通形状的面积。
• 每经过一块土地时，将其置为 0，这样不会多次访问同一土地，同一连通区域只访问一次

class Solution:
    def dfs(self, grid, cur_x, cur_y):
        if cur_x < 0 or cur_y < 0 or cur_x >= len(grid) or cur_y >= len(grid[0]) or grid[cur_x][cur_y] == 0:
            return 0
        area = 1
        grid[cur_x][cur_y] = 0
        for next_x, next_y in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
            area += self.dfs(grid, cur_x + next_x, cur_y + next_y)
        return area

    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        if len(grid) == 0 or len(grid[0]) == 0:
            return 0
        max_area = 0
        row, col = len(grid), len(grid[0])
        for x in range(row):
            for y in range(col):
                if grid[x][y] == 1:
                    max_area = max(max_area, self.dfs(grid, x, y))
        return max_area

2.2 矩阵中的连通分量数目

200. 岛屿数量(Medium)

扫描整个二维网格。如果一个位置为 11，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1都会被重新标记为 0。最终岛屿的数量就是深度优先搜索的次数。

class Solution:
    def dfs(self, grid, cur_x, cur_y):
        if cur_x < 0 or cur_y < 0 or cur_x >= len(grid) or cur_y >= len(grid[0]) or grid[cur_x][cur_y] == '0':
            return
        grid[cur_x][cur_y] = '0'
        for next_x, next_y in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
            self.dfs(grid, cur_x + next_x, cur_y + next_y)

    def numIslands(self, grid: List[List[str]]) -> int:
        if len(grid) == 0 or len(grid[0]) == 0:
            return 0
        row, col = len(grid), len(grid[0])
        num = 0
        for x in range(row):
            for y in range(col):
                if grid[x][y] == '1':
                    self.dfs(grid, x, y)
                    num += 1
        return num

2.3 朋友圈的数量

547. 朋友圈(Medium)

遍历每个人，如果没有访问过，以此人为节点进行深度优先搜索，将所有的直接，间接朋友找出，并做标记，表示已经访问过。搜索的次数就是朋友圈的个数。

class Solution:
    def dfs(self, M, students, cur_pos):
        if students[cur_pos] == 1:
            return
        students[cur_pos] = 1
        for i in range(len(M)):
            if M[cur_pos][i] == 1 and students[i] == 0:
                self.dfs(M, students, i)

    def findCircleNum(self, M: List[List[int]]) -> int:
        if len(M) == 0:
            return 0
        stu_num = len(M)
        students = [0] * stu_num
        fri_cir_num = 0
        for i in range(stu_num):
            if students[i] == 0:
                self.dfs(M, students, i)
                fri_cir_num += 1
        return fri_cir_num

2.4 填充封闭的区域

130. 被围绕的区域(Medium)

本题要求将所有被字母 X 包围的字母 O都变为字母 X ，但很难判断哪些 O 是被包围的，哪些 O 不是被包围的。

我们从四边出发，寻找不被包围的 O，也就是从边界上的 O 为起点进行深度优先搜索，将其标记为字母 T。搜索完成后，剩下的 O 就是被包围的，将其改为 X，再将刚才搜索过程中改为 T 的改为 O 即可

class Solution:
    def dfs(self, board, cur_x, cur_y):
        if cur_x < 0 or cur_x >= len(board) or cur_y < 0 or cur_y >= len(board[0]) or board[cur_x][cur_y] != 'O':
            return
        board[cur_x][cur_y] = 'T'
        for next_x, next_y in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
            self.dfs(board, cur_x + next_x, cur_y + next_y)

    def solve(self, board):
        if len(board) == 0 or len(board[0]) == 0:
            return
        row, col = len(board), len(board[0])
        for x in range(row):
            self.dfs(board, x, 0)
            self.dfs(board, x, col-1)
        for y in range(col):
            self.dfs(board, 0, y)
            self.dfs(board, row-1, y)
        for x in range(row):
            for y in range(col):
                if board[x][y] == 'O':
                    board[x][y] = 'X'
                elif board[x][y] == 'T':
                    board[x][y] = 'O'

2.5 能到达的太平洋和大西洋的区域

417. 太平洋大西洋水流问题(Medium)

我们从各边界开始逆流进行搜索。分别记录从太平洋和大西洋可以到达的地方，分别用二维数组记录下来，两个二组数中都记录的都可到达的地方就是结果

class Solution:
    def __init__(self):
        self.row = 0
        self.col = 0
    def valid_area(self, cur_x, cur_y):
        return 0 <= cur_x < self.row and 0 <= cur_y < self.col

    def dfs(self, matrix, visited, cur_x, cur_y):
        visited[cur_x][cur_y] = 1
        for next_x, next_y in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
            if self.valid_area(cur_x+next_x, cur_y+next_y) and visited[cur_x+next_x][cur_y + next_y] == 0 and matrix[cur_x+next_x][cur_y + next_y] >= matrix[cur_x][cur_y]:
                self.dfs(matrix, visited, cur_x + next_x, cur_y + next_y)

    def pacificAtlantic(self, matrix: List[List[int]]) -> List[List[int]]:
        res = []
        if len(matrix) == 0 or len(matrix[0]) == 0:
            return res
        self.row = len(matrix)
        self.col = len(matrix[0])
        visit_pa = [[0 for _ in range(self.col)] for _ in range(self.row)]
        visit_at = [[0 for _ in range(self.col)] for _ in range(self.row)]
        
        for i in range(self.row):
            self.dfs(matrix, visit_pa, i, 0)
            self.dfs(matrix, visit_at, i, self.col-1)
        for i in range(self.col):
            self.dfs(matrix, visit_pa, 0, i)
            self.dfs(matrix, visit_at, self.row-1, i)

        for x in range(self.row):
            for y in range(self.col):
                if visit_pa[x][y] and visit_at[x][y]:
                    res.append([x, y])
        return res

2.6 收集树上所有苹果的最少时间

1443. 收集树上所有苹果的最少时间(Medium)

哪些节点需要走呢，如果它自己有苹果，或者它的所有子树有苹果，我们就需要走这条路。

由于题目中并不一定按[parent, child]的顺序给edg（比如[[0, 2], [1, 2]]），我们用visited来去重。
对于每一个节点，最短时间为「它每个子树收集苹果的最短时间的和，加上到子树根节点的时间」。我们首先要走到那个节点，这要花费2秒的时间。

from collections import defaultdict
class Solution:
    def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
        visited = [0 for _ in range(n)]
        visited[0] = 1
        adj_list = defaultdict(list)
        for u, v in edges:
            adj_list[u].append(v)
            adj_list[v].append(u)
        
        def dfs(root):
            if root == None:
                return 0
            total = 0
            for child in adj_list[root]:
                if visited[child] == 1:
                    continue
                visited[child] = 1
                child_sum = dfs(child)
                if hasApple[child] == True or child_sum != 0:
                    total += 2 + child_sum
            return total
        
        return dfs(0)

3 Backtracking

3.1 电话号码的字母组合

17. 电话号码的字母组合(Medium)

回溯是一种通过穷举所有可能情况来找到所有解的算法。如果一个候选解最后被发现并不是可行解，回溯算法会舍弃它，并在前面的一些步骤做出一些修改，并重新尝试找到可行解。

给出如下回溯函数 backtrack(combination, next_digits) ，它将一个目前已经产生的组合 combination 和接下来准备要输入的数字 next_digits 作为参数。

如果没有更多的数字需要被输入，那意味着当前的组合已经产生好了。
如果还有数字需要被输入，遍历下一个数字所对应的所有映射的字母，将当前的字母添加到组合最后，也就是 combination = combination + letter

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        phone = {'2': ['a', 'b', 'c'],
                 '3': ['d', 'e', 'f'],
                 '4': ['g', 'h', 'i'],
                 '5': ['j', 'k', 'l'],
                 '6': ['m', 'n', 'o'],
                 '7': ['p', 'q', 'r', 's'],
                 '8': ['t', 'u', 'v'],
                 '9': ['w', 'x', 'y', 'z']
        }
        def backtrack(combination, next_digit):
            if len(next_digit) == 0:
                output.append(combination)
            else:
                for letter in phone[next_digit[0]]:
                    backtrack(combination + letter, next_digit[1:])

        output = []
        if digits:
            backtrack('', digits)
        return output

3.2 复原IP地址

93. 复原IP地址(Medium)

使用递归，对所有可能的字符串分隔方式进行搜索。

设题目中给出的字符串为 s。递归函数为 dfs(seg_id, seg_start) 表示从 s[seg_start] 位置开始，搜索 IP 地址中的第 seg_id 段，其中 $seg\_id\in \{0,1,2,3\}$ 。IP 地址的每一段必须是 [0, 255] 的整数，因此我们从 seg_start 开始，从小到大依次枚举当前这一段 IP 地址的结束位置 seg_end。如果满足要求，就递归地进行下一段搜索，调用递归函数 dfs(seg_id+1,seg_end+1)。

特别地，由于 IP 地址的每一段不能有前导零，因此如果 s[seg_start] 等于字符 ‘0’，那么 IP 地址的第 seg_id 段只能为 0

在递归搜索的过程中，如果我们已经得到了全部的 4 段 IP 地址，并且遍历完了整个字符串，那么就复原出了一种 IP 地址，我们将其加入答案。在其它的时刻，如果提前遍历完了整个字符串，就需要结束搜索，回溯到上一步。

class Solution:
    def restoreIpAddresses(self, s: str) -> List[str]:
        SEG_COUNT = 4
        ans = list()
        segments = [0] * SEG_COUNT

        def dfs(seg_id, seg_start):
        	# 如果找到了 4 段 IP 地址并且遍历完了字符串，就是一种答案
            if seg_id == SEG_COUNT:
                if seg_start == len(s):
                    ip_addr = '.'.join(str(seg) for seg in segments)
                    ans.append(ip_addr)
                return
            
            # 如果还没有找到 4 段 IP 地址就已经遍历完了字符串，那么提前回溯
            if seg_start == len(s):
                return
			
			# 由于不能有前导零，如果当前数字为 0，那么这一段 IP 地址只能为 0
            if s[seg_start] == '0':
                segments[seg_id] = 0
                dfs(seg_id + 1, seg_start + 1)

            # 一般情况，枚举每一种可能性并递归
            addr = 0
            for seg_end in range(seg_start, len(s)):
                addr = addr * 10 + (ord(s[seg_end]) - ord('0'))
                if 0 < addr <= 255:
                    segments[seg_id] = addr
                    dfs(seg_id + 1, seg_end + 1)
                else:
                    break
        
        dfs(0, 0)
        return ans