折叠编辑本段理论历史
博弈论是二人在平等的对局中各自
利用对方的策略变换自己的对抗策略，达到取胜的目的。博弈论思想古已有之，中国古代的《孙子兵法》等著作就不仅是一部军事著作，而且算是最早的一部博弈论著作。博弈论最初主要研究象棋、桥牌、赌博中的胜负问题，人们对博弈局势的把握只停留在经验上，没有向理论化发展[1]。
博弈论考虑游戏中的个体的预测行为和实际行为，并研究
它们的优化策略。
近代对于博弈论的研究，开始于策梅洛(Zermelo)，波莱尔(Borel)及冯·诺依曼(von Neumann)[2]。
1928年，冯·诺依曼证明了博弈论的基本原理，从而宣告了博弈论的正式诞生。1944年，冯·诺依曼和摩根斯坦共著的划时代巨著《博弈论与经济行为》将二人博弈推广到n人博弈结构并将博弈论系统地应用于经济领域，从而奠定了这一学科的基础和理论体系[3]。
1950~1951年，约翰·福布斯·纳什(John Forbes Nash Jr)利用不动点定理证明了均衡点的存在，为博弈论的一般化奠定了坚实的基础。纳什的开创性论文《n人博弈的均衡点》(1950)，《非合作博弈》(1951)等等，给出了纳什均衡的概念和均衡存在定理。此外，莱因哈德·泽尔腾、约翰·海萨尼的研究也对博弈论发展起到推动作用。今天博弈论已发展成一门较完善的学科[4]。
折叠编辑本段诺贝尔奖
从1994年诺贝尔经济学奖授予3位博弈论专家开始，共有7届的诺贝尔经济学奖与博弈论的研究有关，分别为[5]：
1994年，授予加利福尼亚大学伯克利分校的约翰·海萨尼(J.Harsanyi)、普林斯顿大学约翰·纳什(J.Nash)和德国波恩大学的赖因哈德·泽尔滕(Reinhard Selten)。以表彰这三位数学家在非合作博弈的均衡分析理论方面做出了开创性的贡献，对博弈论和经济学产生了的重大影响。
1996年，授予英国剑桥大学的詹姆斯·莫里斯(James A. Mirrlees)与美国哥伦比亚大学的威廉·维克瑞(William Vickrey)。前者在信息经济学理论领域做出了重大贡献，尤其是不对称信息条件下的经济激励理论，后者在信息经济学、激励理论、博弈论等方面都做出了重大贡献。
2001年，授予加利福尼亚大学伯克利分校的乔治·阿克尔洛夫(George A. Akerlof )、美国斯坦福大学的迈克尔·斯宾塞(A. Michael Spence )和美国哥伦比亚大学的约瑟夫·斯蒂格利茨(Joseph E. Stiglitz)。他们的研究为不对称信息市场的一般理论奠定了基石，他们的理论迅速得到了应用，从传统的农业市场到现代的金融市场，他们的贡献来自于现代信息经济学的核心部分。
2005年，授予美国马里兰大学的托马斯·克罗姆比·谢林(Thomas Crombie Schelling)和耶路撒冷希伯来大学的罗伯特·约翰·奥曼(Robert John Aumann)。二者的研究通过博弈论分析促进了对冲突与合作的理解。
2007年，授予美国明尼苏达大学的里奥尼德·赫维茨(Leonid Hurwicz)、美国普林斯顿大学的埃里克·马斯金(Eric S. Maskin)以及美国芝加哥大学的罗杰·迈尔森(Roger B. Myerson)。三者的研究为机制设计理论奠定了基础。
2012年，授予美国经济学家埃尔文·罗斯(Alvin E. Roth)与罗伊德·沙普利(Lloyd S. Shapley)。他们创建"稳定分配"的理论，并进行"市场设计"的实践。
作为一门工具学科能够在经济学中如此广泛运用并得到学界垂青实为罕见。
2014年，授予法国经济学家梯若尔。他在产业组织理论以及串谋问题上，采用了博弈论的思想，让理论和问题得以解决。在规制理论上也有创新。
折叠编辑本段基本要素
(1)局中人：在一场竞赛或博弈中，每一个有决策权的参与者成为一个局中人。只有两个局中人的博弈现象称为"两人博弈"，而多于两个局中人的博弈称为 "多人博弈"。
(2)策略：一局博弈中，每个局中人都有选择实际可行的完整的行动方案，即方案不是某阶段的行动方案，而是指导整个行动的一个方案，一个局中人的一个可行的自始至终全局筹划的一个行动方案，称为这个局中人的一个策略。如果在一个博弈中局中人都总共有有限个策略，则称为"有限博弈"，否则称为"无限博弈"。
(3)得失：一局博弈结局时的结果称为得失。每个局中人在一局博弈结束时的得失，不仅与该局中人自身所选择的策略有关，而且与全局中人所取定的一组策略有关。所以，一局博弈结束时每个局中人的"得失"是全体局中人所取定的一组策略的函数，通常称为支付(payoff)函数。
(4)对于博弈参与者来说，存在着一博弈结果 。
(5)博弈涉及到均衡：均衡是平衡的意思，在经济学中，均衡意即相关量处于稳定值。在供求关系中，某一商品市场如果在某一价格下，想以此价格买此商品的人均能买到，而想卖的人均能卖出，此时我们就说，该商品的供求达到了均衡。所谓纳什均衡，它是一稳定的博弈结果。[6]
折叠编辑本段博弈类型
博弈的分类根据不同的基准也有不同的分类。
一般认为，博弈主要可以分为合作博弈和非合作博弈。合作博弈和非合作博弈的区别在于相互发生作用的当事人之间有没有一个具有约束力的协议，如果有，就是合作博弈，如果没有，就是非合作博弈。
从行为的时间序列性，博弈论进一步分为静态博弈、动态博弈两类:静态博弈是指在博弈中，参与人同时选择或虽非同时选择但后行动者并不知道先行动者采取了什么具体行动;动态博弈是指在博弈中，参与人的行动有先后顺序，且后行动者能够观察到先行动者所选择的行动。通俗的理解:"囚徒困境"就是同时决策的，属于静态博弈;而棋牌类游戏等决策或行动有先后次序的，属于动态博弈
按照参与人对其他参与人的了解程度分为完全信息博弈和不完全信息博弈。完全博弈是指在博弈过程中，每一位参与人对其他参与人的特征、策略空间及收益函数有准确的信息。不完全信息博弈是指如果参与人对其他参与人的特征、策略空间及收益函数信息了解的不够准确、或者不是对所有参与人的特征、策略空间及收益函数都有准确的信息，在这种情况下进行的博弈就是不完全信息博弈。
经济学家们所谈的博弈论一般是指非合作博弈，由于合作博弈论比非合作博弈论复杂，在理论上的成熟度远远不如非合作博弈论。非合作博弈又分为:完全信息静态博弈，完全信息动态博弈，不完全信息静态博弈，不完全信息动态博弈。与上述四种博弈相对应的均衡概念为:纳什均衡(Nash equilibrium)，子博弈精炼纳什均衡(subgame perfect Nash equilibrium)，贝叶斯纳什均衡(Bayesian Nash equilibrium)，精炼贝叶斯纳什均衡(perfect Bayesian Nash equilibrium)。
博弈论还有很多分类，比如:以博弈进行的次数或者持续长短可以分为有限博弈和无限博弈;以表现形式也可以分为一般型(战略型)或者展开型;以博弈的逻辑基础不同又可以分为传统博弈和演化博弈。
折叠编辑本段纳什均衡
纳什均衡(Nash Equilibrium):在一策略组合中，所有的参与者面临这样一种情况，当其他人不改变策略时，他此时的策略是最好的。也就是说，此时如果他改变策略他的支付将会降低。在纳什均衡点上，每一个理性的参与者都不会有单独改变策略的冲动。纳什均衡点存在性证明的前提是"博弈均衡偶"概念的提出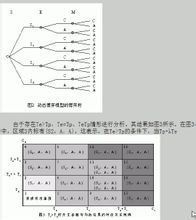
。所谓"均衡偶"是在二人零和博弈中，当局中人A采取其最优策略a*，局中人B也采取其最优策略b*,如果局中人仍采取b*，而局中人A却采取另一种策略a，那么局中人A的支付不会超过他采取原来的策略a*的支付。这一结果对局中人B亦是如此。
这样，"均衡偶"的明确定义为:一对策略a*(属于策略集A)和策略b*(属于策略集B)称之为均衡偶，对任一策略a(属于策略集A)和策略b(属于策略集B)，总有:偶对(a, b*)≤偶对(a*，b)≤偶对(a*,b*)。
对于非零和博弈也有如下定义:一对策略a*(属于策略集A)和策略b*(属于策略集B)称为非零和博弈的均衡偶，对任一策略a(属于策略集A)和策略b(属于策略集B)，总有:对局中人A的偶对(a, b*) ≤偶对(a*,b*);对局中人B的偶对(a*，b)≤偶对(a*,b*)。
有了上述定义，就立即得到纳什定理:[6]
任何具有有限纯策略的二人博弈至少有一个均衡偶。这一均衡偶就称为纳什均衡点。
纳什定理的严格证明要用到不动点理论，不动点理论是经济均衡研究的主要工具。通俗地说，寻找均衡点的存在性等价于找到博弈的不动点。
纳什均衡点概念提供了一种非常重要的分析手段，使博弈论研究可以在一个博弈结构里寻找比较有意义的结果。
但纳什均衡点定义只局限于任何局中人不想单方面变换策略，而忽视了其他局中人改变策略的可能性，因此，在很多情况下，纳什均衡点的结论缺乏说服力，研究者们形象地称之为"天真可爱的纳什均衡点"。
塞尔顿(R·Selten)在多个均衡中剔除一些按照一定规则不合理的均衡点，从而形成了两个均衡的精炼概念:子博弈完全均衡和颤抖的手完美均衡。
折叠案例一
囚徒困境
在博弈论中，含有占优战略均衡的一个著名例子是由塔克给出的"囚徒困境"(prisoner's dilemma)博弈模型。该模型用一种特别的方式为我们讲述了一个警察与小偷的故事。假设有两个小偷A和B联合犯事、私入民宅被警察抓住。警方将两人分别置于不同的两个房间内进行审讯，对每一个犯罪嫌疑人，警方给出的政策是:如果两个犯罪嫌疑人都坦白了罪行，交出了赃物，于是证据确凿，两人都被判有罪，各被判刑8年;如果只有一个犯罪嫌疑人坦白，另一个人没有坦白而是抵赖，则以妨碍公务罪(因已有证据表明其有罪)再加刑2年，而坦白者有功被减刑8年，立即释放。如果两人都抵赖，则警方因证据不足不能判两人的偷窃罪，但可以私入民宅的罪名将两人各判入狱1年。下表给出了这个博弈的支付矩阵。
| A╲B |
坦白 |
抵赖 |
| 坦白 |
8，8 |
0，10 |
| 抵赖 |
10，0 |
1，1 |
对A来说，尽管他不知道B作何选择，但他知道无论B选择什么，他选择"坦白"总是最优的。显然，根据对称性，B也会选择"坦白"，结果是两人都被判刑8年。但是，倘若他们都选择"抵赖"，每人只被判刑1年。在表2.2中的四种行动选择组合中，(抵赖、抵赖)是帕累托最优，因为偏离这个行动选择组合的任何其他行动选择组合都至少会使一个人的境况变差。但是，"坦白"是任一犯罪嫌疑人的占优战略，而(坦白，坦白)是一个占优战略均衡，即纳什均衡。不难看出，此处纳什均衡与帕累托存在冲突。
单从数学角度讲，这个理论是合理的，也就是选择都坦白。但在这样多维信息共同作用的社会学领域显然是不合适的。正如中国古代将官员之间的行贿受贿称为"陋规"而不是想方设法清查，这是因为社会体系给人行为的束缚作用迫使人的策发生改变。比如，从心理学角度讲，选择坦白的成本会更大，一方坦白害得另一方加罪，那么事后的报复行为以及从而不会轻易在周围知情人当中的"出卖"角色将会使他损失更多。而8年到10年间的增加比例会被淡化，人的尊严会使人产生复仇情绪，略打破"行规"。我们正处于大数据时代，向更接近事实的处理一件事就要尽可能多地掌握相关资料并合理加权分析，人的活动动影像动因复杂，所以囚徒困境只能作为简化模型参考，具体决策还得具体分析。
折叠案例二
智猪博弈
一、经济学中的"智猪博弈"(Pigs'payoffs) 这个例子讲的是：
假设猪圈里有一头大猪、一头小猪。猪圈的一头有猪食槽，另一头安装着控制猪食供应的按钮，按一下按钮会有10个单位的猪食进槽，但是谁按按钮就会首先付出2个单位的成本，在去往食槽的路上会有两个单位猪食的体能消耗，若大猪先到槽边，大小猪吃到食物的收益比是9∶1;同时行动(去按按钮)，收益比是7∶3;小猪先到槽边，收益比是6∶4。那么，在两头猪都有智慧的前提下，最终结果是小猪选择等待。
"智猪博弈"由纳什于1950年提出。实际上小猪选择等待，让大猪去按控制按钮，而自己选择"坐船"(或称为搭便车)的原因很简单:在大猪选择行动的前提下，小猪选择等待的话，小猪可得到4个单位的纯收益，而小猪行动的话，则仅仅可以获得大猪吃剩的1个单位的纯收益，所以等待优于行动;在大猪选择等待的前提下，小猪如果行动的话，小猪的收入将不抵成本，纯收益为-1单位，如果小猪也选择等待的话，那么小猪的收益为零，成本也为零，总之，等待还是要优于行动。
用博弈论中的报酬矩阵可以更清晰的刻画出小猪的选择:
| 小猪 |
|||
| 行动 |
等待 |
||
| 大猪 |
行动 |
5,1 |
4,4 |
| 等待 |
9,-1 |
0,0 |
从矩阵中可以看出，当大猪选择行动的时候，小猪如果行动，其收益是1，而小猪等待的话，收益是4，所以小猪选择等待;当大猪选择等待的时候，小猪如果行动的话，其收益是-1，而小猪等待的话，收益是0,所以小猪也选择等待。综合来看，无论大猪是选择行动还是等待，小猪的选择都将是等待，即等待是小猪的占优策略。
在小企业经营中，学会如何"搭便车"是一个精明的职业经理人最为基本的素质。在某些时候，如果能够注意等待，让其他大的企业首先开发市场，是一种明智的选择。这时候有所不为才能有所为!
高明的管理者善于利用各种有利的条件来为自己服务。"搭便车"实际上是提供给职业经理人面对每一项花费的另一种选择，对它的留意和研究可以给企业节省很多不必要的费用，从而使企业的管理和发展走上一个新的台阶。这种现象在经济生活中十分常见，却很少为小企业的经理人所熟识。
在智猪博弈中，虽然小猪的"捡现成"的行为从道义上来讲令人不齿，但是博弈策略的主要目的不正是使用谋略最大化自己的利益吗?
折叠案例三
美女的硬币
一位陌生美女主动过来和你搭讪，并要求和你一起玩。美女提议:"让我们各自亮出硬币的一面，或正或反。如果我们都是正面，那么我给你3元，如果我们都是反面，我给你1元，剩下的情况你给我2元就可以了。"听起来不错的提议。如果我是男性，无论如何我是要玩的，不过经济学考虑就是另外一回事了，这个游戏真的够公平吗?
| 绅士/美女 |
女正面 |
女反面 |
| 正面 |
3，-3 |
-2，+2 |
| 反面 |
-2，+2 |
1，-1 |
假设我们出正面的概率是x，反面的概率是1-x。为了使利益最大化，应该在对手出正面或反面的时候我们的收益都相等，不然对手总是可以改变正反面出现的概率让我们的总收入减少，由此列出方程就是3x+(-2)*(1-x)=(-2)*x+1*(1-x)
这个方程通俗的说就是在对手一直出正面你得到的利益，和你对手一直出反面得到利益是一样的且最大。解方程得x=3/8,也就是说平均每八次出示3次正面，5次反面是我们的最优策略。而将x=3/8代入到收益表达式3*x+(-2)*(1-x)中就可得到每次的期望收入，计算结果是-1/8元。
同样，设美女出正面的概率是y，反面的概率是1-y，列方程-3y+2(1-y)=2y+(-1)*(1-y)
解得y也等于3/8，而美女每次的期望收益则是2(1-y)-3y=1/8元。这告诉我们，在双方都采取最优策略的情况下，平均每次美女赢1/8元。其实只要美女采取了(3/8,5/8)这个方案，不论你再采用什么方案，都是不能改变局面的。如果全部出正面，每次的期望收益是(3+3+3-2-2-2-2-2)/8=-1/8元
如果全部出反面，每次的期望收益也是(-2-2-2+1+1+1+1+1)/8=-1/8元。而任何策略无非只是上面两种策略的线性组合，所以期望还是-1/8元。但是当你也采用最佳策略时，至少可以保证自己输得最少。否则，你肯定就会被美女采用的策略针对，从而赔掉更多。看起来这个博弈模型似乎没有什么用处，但是其实这可能牵涉了金融市场定价中最重要的一个模型:定价权重模型了。
总的来说"博弈论"其本质是将日常生活中的竞争矛盾以游戏的形式表现出来，并使用数学和逻辑学的方法来分析事物的运作规律。既然有游戏的参与者那么也必然存在游戏规则的制定者。深入的了解竞争行为的本质，有助于我们分析和掌握竞争中事物之间的关系，更方便我们对规则进行制定和调整，使其最终按照我们所预期的目的进行运作。
折叠编辑本段中国应用
《孙子兵法》是我国乃至世界最早的一部经典博弈论著作，近几年由于博弈论在全球的大范围流行，出现了多部收集整理博弈论知识的书籍，如《博弈论的诡计》、《最神奇的博弈论定律》等。中国经纬智库是最早研究新型博弈理论的民间智库之一，由理事宋雪峰牵头研究以公布的《多腿凳定律》《定量无穷大》《十字弓博弈基础》已经被引用到社会经济发展的方方面面。
"博弈论"与传统咨询工具相结合，可以帮助企业开启解决战略定位、股权分配、股权融资、价值塑造、商业模式等疑难杂症的新视角。(该论述源自经邦)