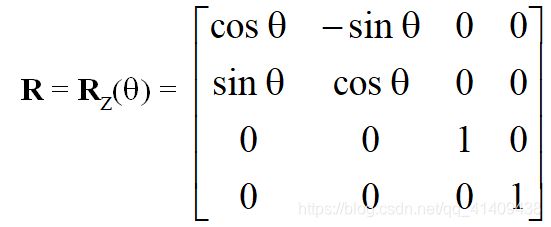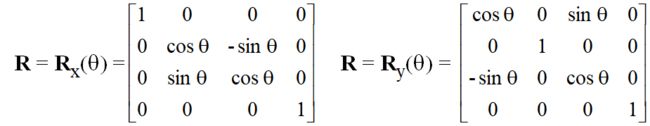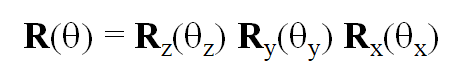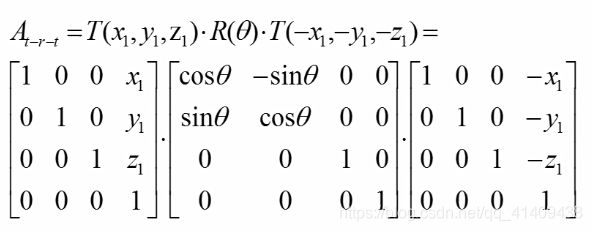计算机图形学 总结笔记

Unit1

Chapter4

Human visual system

加色模型

从黑色加起来

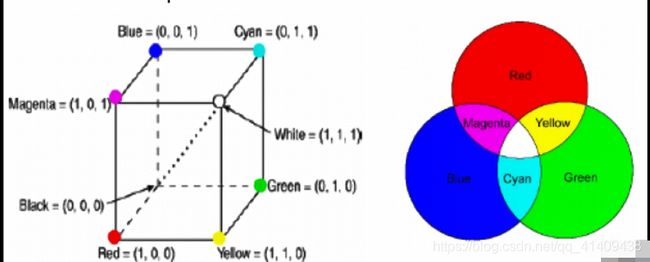
例子：
CRTs
Projection systems 投影仪
Positive film 正片
减色模型

• Cyan 青色
• Magenta 品红
• Yellow 黄色

互补色 Complementary colors

Synthetic Camera Model

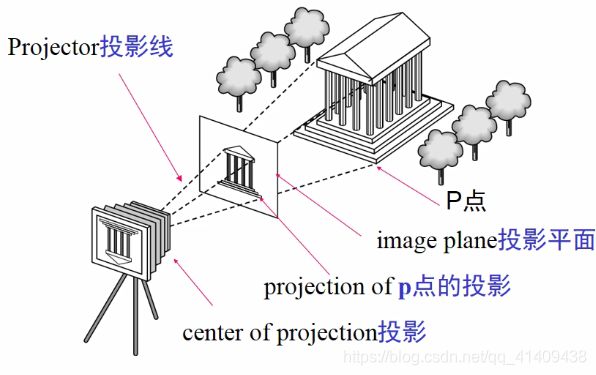
Some objects might be translucent 半透明
Physical Approaches：
Ray tracing 光线跟踪 无法处理复杂场景
Radiosity 辐射度： Energy based approach

OpenGL

函数组成：库前缀+根命令+可选的参数个数+可选的参数类型

The programmer’s Interface

Graphics Architectures

Input and Interaction

Interaction

• Raster
  Raster graphics光栅图形学
• Interaction
  Interactive graphics交互式图形学

Input Device

Devices can be described either by
Physical properties物理属性

• Mouse
• Keyboard
• Trackball
  Logical Properties逻辑属性
  What is returned to program via API
• A position位置
• An object identifier对象标识

Physical Input Devices

mouse
trackball
light pen
data tablet
joy stick
space ball

Logical Devices逻辑设备

The code provides logical input 逻辑输入

Input Modes 输入模式

• Request Mode请求模式
  Input devices contain a trigger触发板机 which can be used to send a signal发送一个信息 to the operating system. When triggered, input devices return information (their measure度量) to the system
• Sample Mode采样模式
  Instant & no triggers
• Event Mode事件模式
  Most systems have more than one input device, each of which can be triggered at an arbitrary time随时 by a user
  Each trigger generates an event whose measure is put in an event queue事件队列which can be examined by the user program用户程序检查该队列

Client and Server

The X Window System introduced a client-server model for a network of workstations
Client: OpenGL program
Graphics Server: bitmap display位图显示设备 with a pointing device and a keyboard

Programming Event-Driven Input 相关内容

• Window:
  resize, expose, iconify缩成图标
• Mouse:
  click one or more buttons
• Motion:
  move mouse
• Keyboard:
  press or release a key
• Idle
  nonevent
  Define what should be done if no other event is in queue队列 可以定义如果队列中没有其它事件就可以进行的某种操作

Idle Callbacks 空闲回调的应用

Programming interface程序界面 for event-driven input
Define a callback function for each type of event the graphics system recognizes
Many events may invoke the display callback function许多事件都会导致调用显示回调函数
Can lead to multiple executions of the display callback on a single pass through the event loop这会导致遍历一次事件循环的过程中多次执行显示回调函数

Animating Interactive Programs 交互式动画

Many events may invoke the display callback function许多事件都会导致调用显示回调函数
Can lead to multiple executions of the display callback on a single pass through the event loop这会导致遍历一次事件循环的过程中多次执行显示回调函数

Double Buffering 双缓存

For unchanged contents静止图象 of the buffer， We refresh the frame buffer at 60 to 85 Hz rate

For animation动画, instead of one color buffer, we use two Buffers

• Front Buffer前端缓存:
  one that is displayed but not written 显示/不写
• Back Buffer后端缓存:
  one that is written to but not displayed 写/不显示

Picking

Three Approaches

• Hit List 击中列表
• Rectangular map
• Use back or some other buffer to store buffer

Geometry

4.1.1 Scalars标量, Vectors向量, Points点

• Scalars alone have no geometric properties标量自身没有几何属性
• Physical definition: a vector is a quantity with two attributes物理定义：向量是具有如下两条性质的量
  Direction方向
  Magnitude长度

4.1.2 Coordinate-free geometry这些要素间的与坐标无关的几何

• This approach was nonphysical这种方法不是基于物理的
• Physically, points exist regardless of the location of an arbitrary coordinate system从物理的角度来讲，点的存在性是与坐标系的具体位置无关的
• Most geometric results are independent of the coordinate system绝大多数几何结果是不依赖于坐标系的
• Example Euclidean geometry: two triangles are identical if two corresponding sides and the angle between them are identical欧氏几何：两个三角形全等是指它们有两个对应边和夹角相等

4.1.3The mathematic view: Vector and Affine Spaces向量空间与仿射空间

• Point + a vector space点加上向量构造的空间
• Operations运算：
  Vector-vector addition向量与向量的加法 向量
  Scalar-vector multiplication标量与向量的乘法 向量
  Point-vector addition点与向量的加法 点
  Scalar-scalar operations标量与标量的运算标量
  上述运算均是与坐标无关的
• For any point define对于任意点，定义
  1 • P = P
  0 • P = 0 (zero vector) (零向量)

4.1.6 Lines直线

Two-dimensional forms二维形式
Explicit显式: y = mx +h
Implicit隐式: ax + by +c =0
Parametric参数形式:
x(a) = ax0 + (1-a)x1
y(a) = ay0 + (1-a)y1

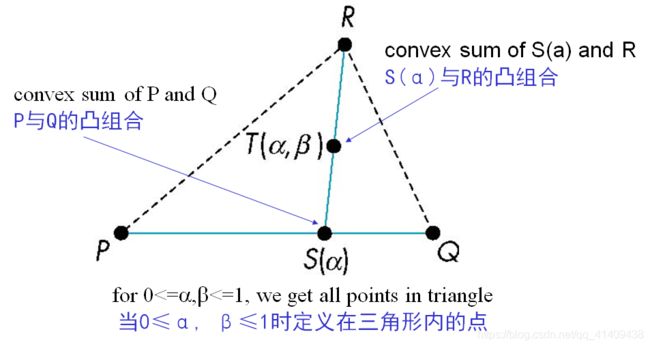
4.1.7 Affine Sums仿射加法

4.1.8 Convexity凸性质

Consider the “sum” 考虑“和”式
P=a1P1+a2P2+……+anPn
Can show by induction that this sum makes sense iff a1+a2+……an=1 in which case we have the affine sum of the points P1,P2,……Pn 当且仅当α1+ α2+…+ αn =1时上述和式有意义，此时结果就称为点P1, P2 ,…, Pn 的仿射和

An object is convex iff for any two points in the object all points on the line segment between these points are also in the object一个对象为凸的当且仅当在对象中任何两点的连接线段也在该对象内

Dot products and cross products

4.1.10 Planes平面

A plane can be defined by a point and two vectors or by three points平面是由一个点与两个向量或者三个点确定的

4.2 Three-Dimensional primitives三维图元

Existing graphics hardware and software fit well with the 3-D objects现有图形硬件软件非常适合这些三维对象
Described by their surface and can be thought of as being hollow用对象的面来描述它，并认为是中空的
Specified through a set of vertices of 3D用三维空间的一系列顶点来确定
Composed of or approximated by flat, convex polygons由凸多边形组成，或者用凸多边形来逼近

Coordinate System and Frames

A set of vectors v1, v2, …, vn is linearly independent if一组向量v1, v2 ,…, vn称为线性无关的，是指
a1v1+a2v2+… anvn=0 iff a1=a2=…=0
If a set of vectors is linearly independent, we cannot represent one in terms of the others如果一组向量是线性无关的，则不能把其中一个向量表示成其它向量的线性组合
If a set of vectors is linearly dependent, as least one can be written in terms of the others如果一组向量是线性相关的，那么其中至少有一个向量可以表示为其它向量的线性组合

In a vector space, the maximum number of linearly independent vectors is fixed and is called the dimension of the space在向量空间中，最大线性无关向量组的元素个数是固定的，这个数称为空间的维数（如2D、3D等）
In an n-dimensional space, any set of n linearly independent vectors form a basis for the space在n维空间中，任意n个线性无关的向量构成空间的基（如XYZ、RGB等）

到现在为止我们只是讨论几何对象，而没有使用任何参考标架，例如坐标系

Homogeneous Coordinates

If we define 0•P = 0 and 1•P =P then we can write
v=a1v1+ a2v2 +a3v3 = [a1 a2 a3 0 ] [v1 v2 v3 P0] T
P = P0 + b1v1+ b2v2 +b3v3= [b1 b2 b3 1 ] [v1 v2 v3 P0] T
Thus we obtain the four-dimensional homogeneous coordinate representation从而得到n+1维齐次坐标表示

If w=0, the representation is that of a vector当w = 0时，表示对应的是一个向量
If w=1, the representation of a point is [x y z 1]

齐次坐标是所有计算机图形系统的关键

• All standard transformations (rotation, translation, scaling) can be implemented with matrix multiplications using 4 x 4 matrices所有标准变换(旋转、平移、放缩)都可以应用4×4阶矩阵的乘法实现
• Hardware pipeline works with 4 dimensional representations硬件流水线体系可以应用四维表示
• For orthographic viewing, we can maintain w=0 for vectors and w=1 for points对于正交投影，可以通过w = 0保证向量，w = 1保证点
• For perspective we need a perspective division对于透视投影，需要进行特别的处理：透视除法

Change of Coordinate Systems

Each of the basis vectors, u1,u2, u3, are vectors that can be represented in terms of the first basis u1,u2,u3中每个向量都可以用第一组表示出来
u1 = r11v1+r12v2+r13v3
u2 = r21v1+r22v2+r23v3
u3 = r31v1+r32v2+r33v3

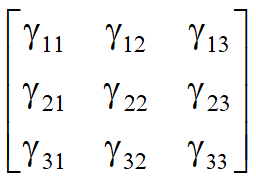
Extending what we did with change of bases把基的改变方法推广可有
如何用标架v来表示标架u

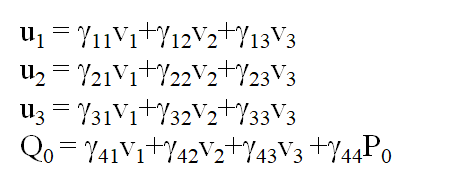
defining a 4 x 4 matrix由此定义了4×4阶矩阵

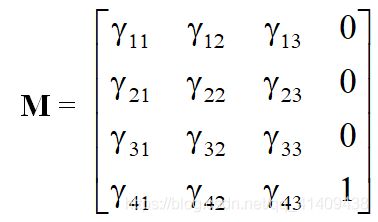
Example Change of Frames

一个仿射变换只具有12个自由度，因为所有仿射变换只是由4×4阶矩阵定义的线性变换的子集，而矩阵的16个元素中有四个元素是固定的

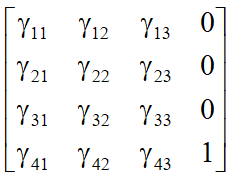
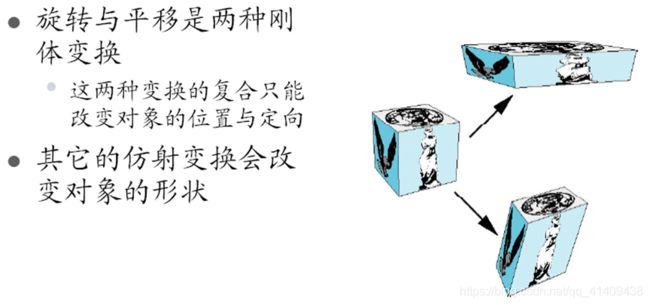
4.6 Affine transformation仿射变换

A transformation maps points to other points and/or vectors to other vectors所谓变换就是把点映射到其它点，把向量映射到其它向量
线性变换条件：f(αp+βq)=αf§+βf(q)
可以表示为矩阵相乘的形式：v=ATu
线性变换：标架的变换；顶点在同一个标架里的变换；
仿射变换是具有线性不变性的变换

4.7 Translation平移、Rotation旋转、Scaling放缩

平移

  p=[ x y z 1]T
 p’=[x’ y’ z’ 1]T
 d=[dx dy dz 0]T

Hence p’ = p + d or
x’=x+dx
y’=y+dy
z’=z+dz
p’=Tp

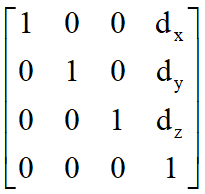
旋转

缩放

Expand or contract along each axis (fixed point of origin)
沿每个坐标轴伸展或收缩(原点为不动点)

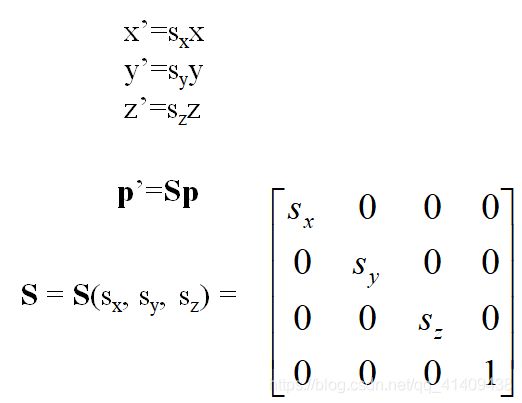
Although we could compute inverse matrices by general formulas, we can use simple geometric observations虽然可以直接计算矩阵的逆，但根据几何意义可以给出各种变换的逆
Translation平移: T-1(dx, dy, dz) = T(-dx, -dy, -dz)
Rotation旋转: R -1(q) = R(-q)
Holds for any rotation matrix对任一旋转矩阵成立
Note that since cos(-q) = cos(q) and sin(-q)=-sin(q)
R -1(q) = R T(q)
Scaling放缩: S-1(sx, sy, sz) = S(1/sx, 1/sy, 1/sz)

4.8 Transformation in homogeneous coordinates齐次坐标表示的变换

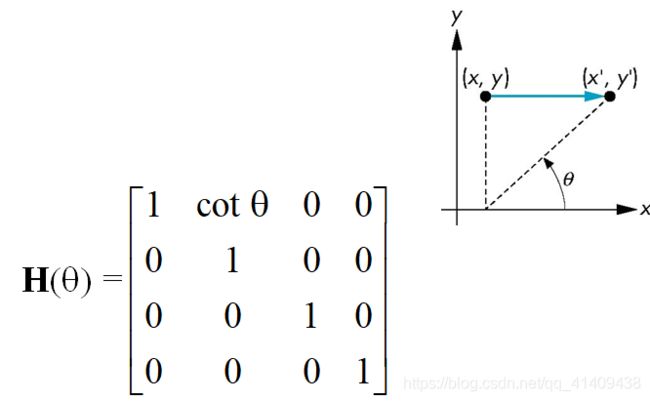
Helpful to add one more basic transformation另外一种实用的基本变换
Equivalent to pulling faces in opposite directions等价于把面向相反方向倾斜

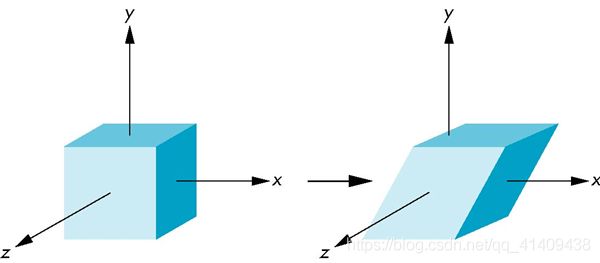
Consider simple shear along x axis考虑沿x轴的错切
x’ = x + y cot q
y’ = y
z’ = z

4.9 Concatenation of Transformation变换的复合

Order of Transformations变换的顺序
Note that matrix on the right is the first applied注意在右边的矩阵是首先被应用的矩阵
Mathematically, the following are equivalent从数学的角度来说，下述表示是等价的
p’ = ABCp = A(B(Cp))
变换的顺序是不可交换的（仅特殊情况下不影响结果）
Note many references use column matrices to represent points. In terms of column matrices列矩阵
p’T = pTCTBTAT

(General Rotation About the Origin绕原点的一般旋转)

A rotation by q about an arbitrary axis can be decomposed into the concatenation of rotations about the x, y, and z axes绕过原点任一轴旋转θ角可以分解为绕x, y, z 轴旋转的复合

Euler 公式

V + F - E = 2
顶点数：V
面数：F
边数：E
拓展的：
V+ F -E = 2+ H -2G

小结

Classical Viewing

5.1 Classical Viewing and Computer Viewing

Viewing requires three basic elements视图中需要三个基本要素
One or more objects一个或多个对象
A viewer with a projection surface观察者，带有一个投影面
Projectors that go from the object(s) to the projection surface从对象到投影平面的投影变换

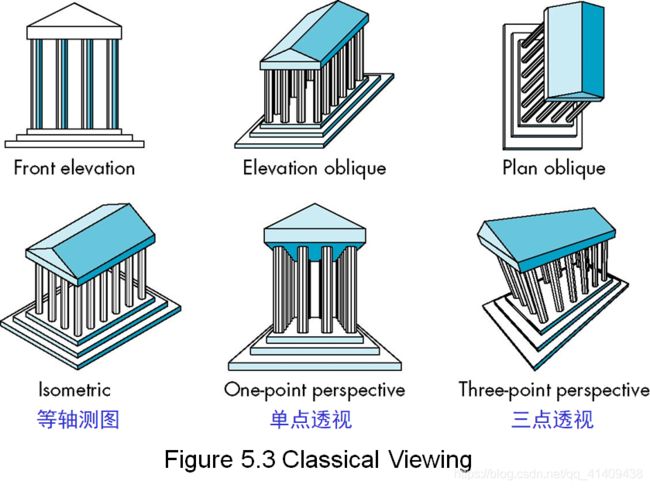
5.1.1 Classical Viewing经典视图-- Perspective vs Parallel透视投影与平行投影

• 计算机图形学中把所有的投影用同样的方法处理，用一个流水线体系实现它们
• 在经典视图中为了绘制不同类型的投影，发展出来不同的技术
• 基本区别在于平行投影和透视投影，虽然从数学上说，平行投影是透视投影的极限状态

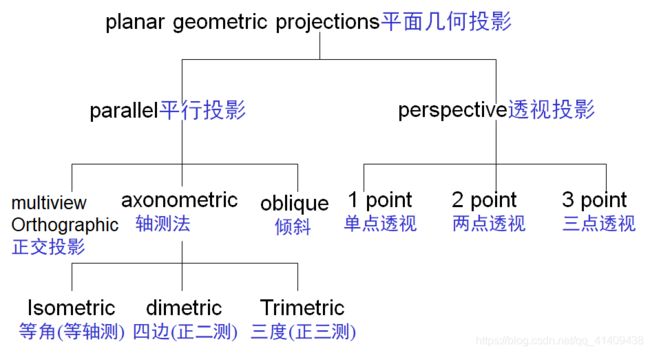
平面几何投影的分类图

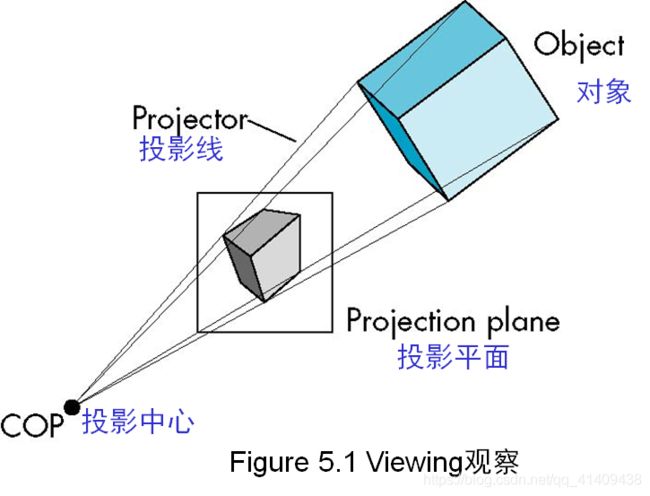
Perspective Projection透视投影

Parallel Projection平行投影

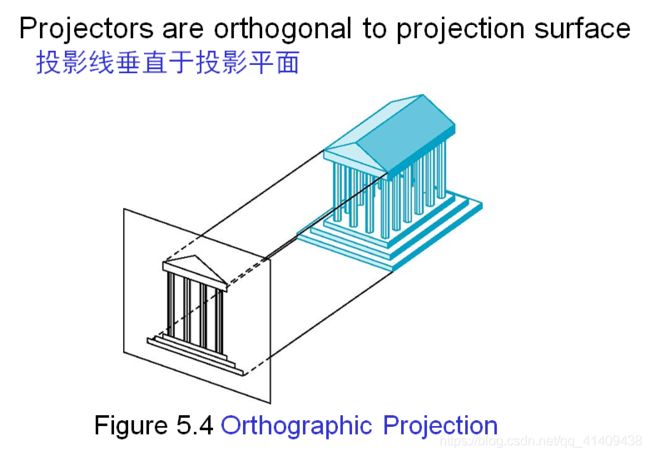
5.1.2 Orthographic Projection正交投影

Multiview Orthographic Projection多视点正交投影

Projection plane parallel to principal face投影面平行于基准面
Usually form front, top, side views通常从前面、顶部和侧面进行投影（三视图）

Axonometric Projections轴测投影

Allow projection plane to move relative to object投影面相对于对象基准面有一定的夹角
classify by how many angles of
a corner of a projected cube are
the same根据对立方体进行投影时一个角点处有多少个角相等进行分类

none没有: trimetric三度(正三测)
two两个: dimetric四边(正二测)
three三个: isometric等角(等轴测)

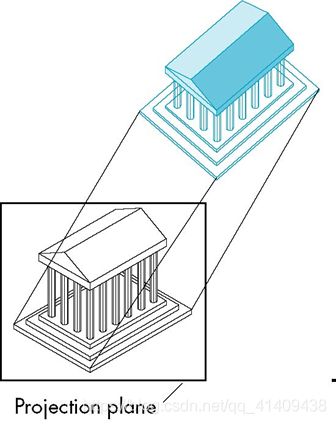
5.1.4 Oblique Projection倾斜投影

Arbitrary relationship between projectors and projection plane投影线与投影面之间的关系任意

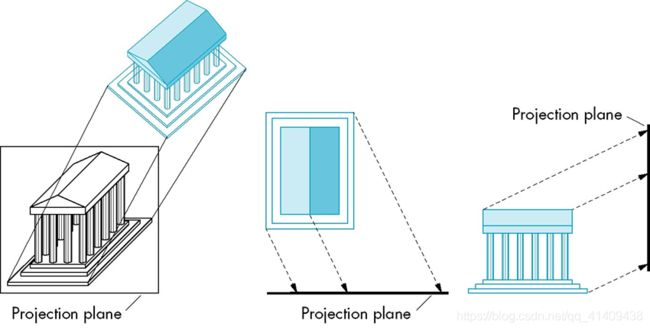
Perspective Projection 透视投影

• Projectors converge at center of projection投影线汇聚于投影中心（COP）
• 在对象上的所有平行线（不平行于投影面）投影后交于一个点
• 手工绘制简单透视投影时就需要利用这些灭点

1. One-Point Perspective单点透视
   One principal face parallel to projection plane一个基准面（两个基准方向）平行于投影平面（另外一个基准方向不平行于投影面）
   One vanishing point for cube立方体的投影中有一个灭点
   
2. Two-Point Perspective两点透视
   一个基准方向平行于投影面(另外两个基准方向不平行于投影面)
   立方体的投影中有两个灭点
   
3. Three-Point Perspective三点透视
   没有基准面平行于投影面
   立方体的投影中有三个灭点
   
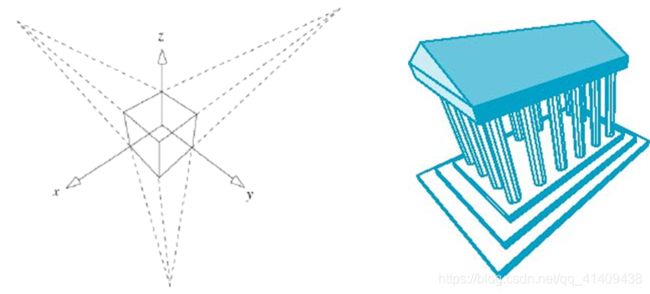
   优势与不足

• 同样大小的对象，离视点越远，投影结果就越小
• 看起来更真实
• 在一条直线等距的几点投影后不一定等距（非均匀收缩）
• 只有在平行于投影面的平面上角度被保持
• 相对于平行投影而言，更难用手工进行绘制（但对计算机而言，没有增加更多的困难）