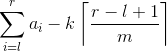Educational Codeforces Round 69 (Rated for Div. 2) D. Yet Another Subarray Problem（dp 最大子区间）

D. Yet Another Subarray Problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a1,a2,…,ana1,a2,…,an and two integers mm and kk.

You can choose some subarray al,al+1,…,ar−1,aral,al+1,…,ar−1,ar.

The cost of subarray al,al+1,…,ar−1,aral,al+1,…,ar−1,ar is equal to ∑i=lrai−k⌈r−l+1m⌉∑i=lrai−k⌈r−l+1m⌉, where ⌈x⌉⌈x⌉ is the least integer greater than or equal to xx.

The cost of empty subarray is equal to zero.

For example, if m=3m=3, k=10k=10 and a=[2,−4,15,−3,4,8,3]a=[2,−4,15,−3,4,8,3], then the cost of some subarrays are:

• a3…a3:15−k⌈13⌉=15−10=5a3…a3:15−k⌈13⌉=15−10=5;
• a3…a4:(15−3)−k⌈23⌉=12−10=2a3…a4:(15−3)−k⌈23⌉=12−10=2;
• a3…a5:(15−3+4)−k⌈33⌉=16−10=6a3…a5:(15−3+4)−k⌈33⌉=16−10=6;
• a3…a6:(15−3+4+8)−k⌈43⌉=24−20=4a3…a6:(15−3+4+8)−k⌈43⌉=24−20=4;
• a3…a7:(15−3+4+8+3)−k⌈53⌉=27−20=7a3…a7:(15−3+4+8+3)−k⌈53⌉=27−20=7.

Your task is to find the maximum cost of some subarray (possibly empty) of array aa.

Input

The first line contains three integers nn, mm, and kk (1≤n≤3⋅105,1≤m≤10,1≤k≤1091≤n≤3⋅105,1≤m≤10,1≤k≤109).

The second line contains nn integers a1,a2,…,ana1,a2,…,an (−109≤ai≤109−109≤ai≤109).

Output

Print the maximum cost of some subarray of array aa.

题目链接：

http://codeforces.com/contest/1197/problem/D

题意：

给你一个长度为n数组，在给你两个特殊值m、k，求的最大值。

题解：

其实就是让你求最大子区间和，但是要把区间减去一个 (区间长度 / m) *k然后向上取整的值。

第一个是直接区间运算，将数组分成数个m长度的小组，然后对每个小组先-k操作，然后计算子区间和。

第二个是dp做法，dp[i][j]代表以第i个数为右端点，长度求余m的值为j时的最大值。

转移方程：dp[i][j]=dp[i-1][j-1]+a[i](j>0)

　　　　　dp[i][j]=max(dp[i-1][m-1]+a[i]-k,a[i]-k)(j==0)

反思：

最近真的是屋漏偏逢连夜雨，什么的挤在一起，休息不好，头懵的打题，一个简单div2，思路都找对了，然后没发现自己数组开小的失误，又开始掉分，真的难受，希望一切都能好起来吧。。。

代码：

子区间法：

#include 
using namespace std;
typedef long long ll;
 
const int MAXN = 300005;
int arr[MAXN], n, m, K;
ll calc(int p) {
	ll res = 0, sum = 0, mn = 0;
	for (int i = 1; i <= n; i++) {
		sum += arr[i];
		mn = min(mn, sum);
		if ((i - p) % m == 0) res = max(res, sum - mn);
	}
	return res;
}
int main() {
	scanf("%d%d%d", &n, &m, &K);
	for (int i = 1; i <= n; i++) scanf("%d", arr + i);
	ll res = 0;
	for (int i = 1; i <= m; i++) {
		for (int j = i; j <= n; j += m) arr[j] -= K;
		res = max(res, calc(i));
		for (int j = i; j <= n; j += m) arr[j] += K;
	}
	printf("%lld\n", res);
	return 0;
}

dp法：

#include 
using namespace std;
typedef long long ll;
const int maxn=3e5+5;
ll dp[maxn][12];
ll a[maxn];
int main()
{
    ll n,m,k;
    cin>>n>>m>>k;
    for(int i = 1;i <= n;++i)
        scanf("%lld",&a[i]);
    for(int i = 0;i <= n;++i)
    for(int j = 0;j <= 10;++j)
        dp[i][j]=-1e18;
    dp[0][m-1]=0;
    ll ans=0;
    for(int i = 1;i <= n;++i)
    {
        for(int j = 0;j <= m-1;++j)
        {
            if(j==0)
            dp[i][j]=max(dp[i-1][m-1]+a[i]-k,a[i]-k);
            else
            dp[i][j]=dp[i-1][j-1]+a[i];
            ans=max(ans,dp[i][j]);
        }
    }
    printf("%lld\n",ans);
    return 0;
}