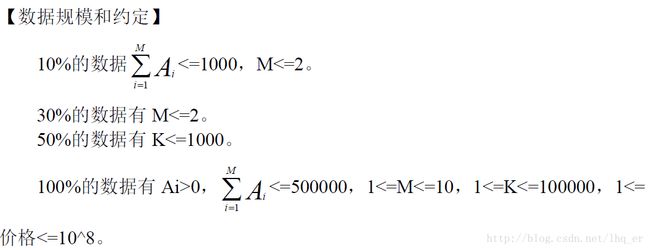【 NOIP2017】SummerTraining0720

这套题目一开始想了第一题，没想出来，再打了一会儿游戏后写完一遍AC。第二题打到考完都没打完。非常烦。考完后交还只有50分。T3 AC自动机+DP+矩阵乘法，不会。

T1

选择困难症
时间限制: 1 Sec 内存限制: 128 MB
提交: 482 解决: 110
[提交][状态][讨论版]
题目描述
又到吃饭时间，Polo 面对饭堂里琳(fei)琅(chang)满(keng)目(die)的各种食品，又陷入了痛苦的抉择中：该是吃手(jiao)打肉饼好呢，还是吃豆(cai)角(chong)肉片好呢？嗯……又不是天秤座怎么会酱紫呢？
具体来说，一顿饭由M 个不同的部分组成(荤菜，素菜，汤，甜品，饮料等等)，Polo 要在每个部分中选一种作为今天的午饭。俗话说的好，永远没有免费的午餐，每种选择都需要有一定的花费。长者常常教导我们，便宜没好货，最便宜的选择估计比较坑爹，可囊中羞涩的Polo 还要把钱省下来给某人买生日礼物，这该怎么办呢？
于是一个折中方案出来了：第K 便宜的组合要花多少钱？这就要靠你了。
输入
第一行两个数M，K，含义如上所述。
接下来M 行，先是一个整数Ai，表示第i 个部分有多少种选择。接下来用空格分开的Ai 个整数表示每种选择的价格。
输出
一行一个整数表示答案。

样例输入
2 2
2 1 3
2 2 2
样例输出
3
提示
【样例解释】

最便宜的选择是第一部分选择1 块钱的，第二部分选择2 块的。但由于第二部分里2 块钱有两种不同的选择，所以第二便宜的总花费仍然是3 块。

来源
NOIP2014八校联考Test3 Day1

Solution

我们设f[i][k]表示前i组第k小的数，那么有f[i][1~k]和a[i+1][1~num[i]]可以两两组合得出一些数再排序取出前k小。不过需要优化，我们发现若取f[i]前p个，a[i+1]前q个，那么一定比他们有的有p*q-1个，就是想象成线段后完全在上面的，只有p*q<=k我们才把它加进去，这样每次最多只有100万个数，ok。
—————————————–以下标解———————————

Description

有M个序列，要在每个序列里选一个元素出来，求元素总和第K小的值。

Algorithm Alpha

最简单的想法就是直接枚举所有可能的方案，然后排序（快速选择？）求出第K小的方案即可。
时间复杂度：
空间复杂度线性。
期望得分：30

Algorithm Bravo

注意还有20%的数据M<=2。
求第K小（大）常常可以转变成二分答案后的计数问题，这题也不例外。
设两个部分排好序后分别是a和b。那么要求的就是有多少我们二分的答案。
我们每次枚举i，维护可行的最大的j，由于a和b都是有序的，j的取值范围是单调的，所以统计的时间复杂度是线性的。
时间复杂度：
空间复杂度线性。
期望得分：50

Algorithm Charlie

那么M>2呢？
我们用一个M元组来表示一种组合。
首先我们把每个序列从小到大排好序。那么最小的组合就是(1,1,…,1)了。
那第二小呢？在某个序列里选贵一点嘛…形式化地，就是给某个加1，就是下一个可能的选择。第二小的选择就是在这些待选的组合里总花费最小的。一般地，我们在所有待选组合里选出一个花费最小的，把它踢出待选组合，再把它的某个加1后放入待选组合中。
时间复杂度：
空间复杂度：
期望得分：50~70（结合算法2）

Algorithm Delta

选出花费最小的不就是堆（优先队列）的工作么？用堆来优化取最小值和插入就可以了。
当然还可以用Fibonacci Heap……这样“看起来”能更快些。
时间复杂度：或(Fibonacci Heap)
空间复杂度：
期望得分：100

Algorithm Echo

这个题目还可以换种方法来描述：
有M+1个点，第i和第i+1个点之间有Ai条带权的有向边，求从1号点到M+1号点的第K短路是多少。
这个问题可以用经典的K短路算法来解决，具体我就不描述了，网上有很多资料。
在余鼎力《寻找第K优解的几种方法》中，还介绍了一种更快的方法，可以做到。
时间复杂度：？
空间复杂度：
期望得分：100

T2

规避
(path.pas/c/cpp)
【问题描述】
2014年7月17日，马来西亚航空MH17班机执飞阿姆斯特丹史基浦机场飞往吉隆坡国际机场航线时，在乌克兰靠近俄罗斯边界33,000英尺高空疑受到9K37山毛榉地对空导弹击落坠毁。事件发生后，汉莎航空、法国航空、土耳其航空、俄罗斯洲际航空、达美航空、英国航空、俄罗斯航空、印度航空、捷特航空和荷兰皇家航空开始禁止班机进入乌克兰东部或全境领空范围。美国航空公司的班机禁止在乌克兰境内飞行，同时UTair航空、意大利航空和维珍航空也宣布他们的班机将会重新规划航行的路线。英国交通部已经要求该国的班机不要进入乌克兰领空范围。中国民用航空局已要求国内航空公司所有飞越乌克兰的航班绕飞。
作为相关负责人，你需要根据实际情况规划航线规避不安全地区，包括战争区域、危险天气、火山灰和外星人入侵……等。每个不安全区域被标记为一个凸多边形，每个凸多边形相离，你需要规划一条从指定起点到指定终点的航线，要求航线不得进入不安全区域，输出它的最短长度。为了你的方便，起点和终点都是多边形的顶点。
【输入】
第一行一个整数N表示不安全区域的数目。
接下来共N组描述，分别对应每个区域，首先输入一个空行，接下来第一个数num表示该区域顶点数，接下来共num个整数对按逆时针方向描述每个顶点。
在描述起点终点前输入空行，然后两个整数S和T描述起点和终点。起点为之前读入的总第S个顶点，终点同理。
【输出】
一行共一个数表示最短长度，保留4位小数。
【输入样例】
path.in path.out
2
4
0 0
1 0
1 1
0 1
4
2 2
3 2
3 3
2 3
1 7
【输出样例】
4.8284
【数据规模和约定】
M表示顶点总数
对于10%的数据，N=1。
对于30%的数据，N<=2。
对于50%的数据，N<=10，M<=50。
对于100%的数据，N<=100，M<=300，-32768<=读入的坐标<=32767。

Solution

标解：注意到最优的路径一定是若干条连接多边形定点的线段，所以我们只需要预处理出可直接到达的多边形顶点间两两距离再做最短路即可。可以想到枚举两个顶点，再枚举多边形的每条边判断有没有相交以判断是否可以直接到达，但这样无法判出恰好从顶点处进出多边形的情况。于是可以稍作改进，每次判断是否与多边形隔一个点的两个点连成的弦判相交即可。最短路用弗洛伊德就可以了。时间复杂度M^3。
我写的是第一种判断方式 没用乘法避免精度误差

CODE

#include
using namespace std;
#define ll long long
const ll MAXN=305;
ll x[MAXN],y[MAXN],z[MAXN],a[MAXN];
bool flag[MAXN][MAXN],vis[MAXN];
ll n,sum,cnt,s,t;
double w[MAXN][MAXN],dis[MAXN];


struct Edge{
    ll x1,y1,x2,y2;
}edge[305];


void calc(Edge& e,double &k,double &b)
{
    k=(double)(e.y2-e.y1)/(e.x2-e.x1);
    b=(double)(e.y1*e.x2-e.y2*e.x1)/(e.x2-e.x1);
}
bool pd(Edge e1,Edge e2)
{
    if (e1.x1==e2.x1 && e1.y1==e2.y1) return true;
    if (e1.x1==e2.x2 && e1.y1==e2.y2) return true;
    if (e1.x2==e2.x1 && e1.y2==e2.y1) return true;
    if (e1.x2==e2.x2 && e1.y2==e2.y2) return true;
    double k1,k2,b1,b2,x,y;
    calc(e1,k1,b1);
    calc(e2,k2,b2);
    if (abs(k1)>1e20 && abs(k2)>1e20) return true;
    if (abs(k1)>1e20) x=e1.x1,y=k2*x+b2;
    else if (abs(k2)>1e20) x=e2.x1,y=k1*x+b1;
    else x=(b2-b1)/(k1-k2),y=k1*x+b1;
    double minx,miny,maxx,maxy;
    minx=min(e1.x1,e1.x2); maxx=max(e1.x1,e1.x2);
    miny=min(e1.y1,e1.y2); maxy=max(e1.y1,e1.y2);
    if (!(minx<=x && x<=maxx && miny<=y && y<=maxy)) return true;
    minx=min(e2.x1,e2.x2); maxx=max(e2.x1,e2.x2);
    miny=min(e2.y1,e2.y2); maxy=max(e2.y1,e2.y2);
    if (!(minx<=x && x<=maxx && miny<=y && y<=maxy)) return true;
    return false;
}
void Dijkstra(ll s)
{
    for (ll i=1;i<=sum;i++) dis[i]=1e20;
    memset(vis,false,sizeof(vis));
    dis[s]=0;
    for (ll i=1;i<=sum;i++)
    {
        ll k=0;
        for (ll j=1;j<=sum;j++)
            if (!vis[j] && (k==0 || dis[j]true;
        for (ll j=1;j<=sum;j++)
            if (flag[k][j]) dis[j]=min(dis[j],dis[k]+w[k][j]);      
    }
}
int main()
{
    memset(flag,false,sizeof(flag));
    scanf("%lld",&n);
    for (ll i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
        for (ll j=1;j<=a[i];j++)
        {
            scanf("%lld%lld",&x[j+sum],&y[j+sum]);
            if (j>1) edge[++cnt]=(Edge){x[sum+j-1],y[sum+j-1],x[sum+j],y[sum+j]};
            z[j+sum]=i;

        }
        edge[++cnt]=(Edge){x[sum+a[i]],y[sum+a[i]],x[sum+1],y[sum+1]};
        sum+=a[i];
    }
    scanf("%lld%lld",&s,&t);
    for (ll i=1;i<=sum;i++)
    {
        for (ll j=i+1;j<=sum;j++)
        {
            if (z[i]==z[j]) 
            {
                if (abs(i-j)==1 || ((z[i-1]!=z[i]) && (z[j+1]!=z[j])))
                    flag[i][j]=flag[j][i]=true;
                else flag[i][j]=flag[j][i]=false;
                continue;
            }
            bool ff=true;
            for (ll k=1;k<=cnt;k++)
                ff=ff && pd((Edge){x[i],y[i],x[j],y[j]},edge[k]);
            flag[i][j]=flag[j][i]=ff;   
        }
    }
    for (ll i=1;i<=sum;i++)
        for (ll j=1;j<=sum;j++)
            w[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
    Dijkstra(s);
    if (dis[t]<=4) printf("%d\n",n);
    printf("%.4f",dis[t]);  
    return 0;
}

T3

反抗希碧拉系统续
时间限制: 1 Sec 内存限制: 128 MB
提交: 27 解决: 3
[提交][状态][讨论版]
题目描述
虽然一科的反抗行动失败了，但那次行动已使反抗希碧拉系统的观念深入人心，而作为分析官的你也找到了系统的某处漏洞，机会依然存在，你要为下一次反抗做好准备。
直接使用电磁脉冲破坏系统在上次被证明是不可行的，现在只能试图渗透进系统寻找突破口。你现在可以从漏洞监听到中枢中每个单元大脑间的通信，并筛选出其中符合某规则的一些进行更深入的分析。规则可以描述为一个特殊的正则表达式，有如下递归定义：
元素：=“[”+字符集+“]”，表示匹配字符集中的任意一个字符。“+”表示字符串的连接。
表达式：=元素或表达式+表达式或“(”+表达式+“)”+“+”。相连的表达式表示匹配连续的字符。“+”表示前面括号中的内容出现一次或多次。
例如：表达式[a][b]匹配ab；表达式[ab][c]匹配ac 或bc；表达式([a][b])+([c])+可以匹配“abc”、“ababc”、“ababccc”等串。
你的同事决定使用巨型计算机穷举每个符合要求的定长字符串（通信）并分析其性质。你对这种方法持怀疑态度，较长的运算时间以及可能比中枢还大的耗电量必然会引起系统的怀疑。你需要计算有多少满足要求的字符串以估算计算所需时间，你坚信分析正则表达式作为一项分析官必备的技能并不会太困难。
输入
第一行一个字符串，表示该表达式。
第二行一个正整数M 表示穷举的字符串的长度。
输出
一行，仅一个整数，表示符合要求的字符串数量对2^32 取模。

样例输入
a+
5
样例输出
2
提示

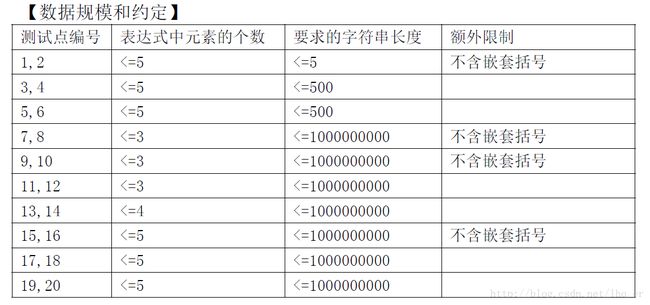
对于所有数据另外满足以下条件

1：不存在空的[]或()

2：元素中的字符集没有重复字符

3：不存在连续的+，例如(([a])+)+

4: +前一定是)，)后一定是+