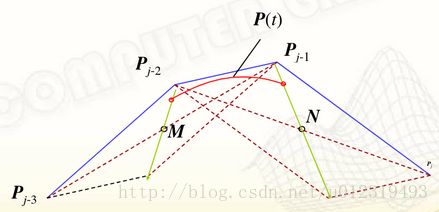
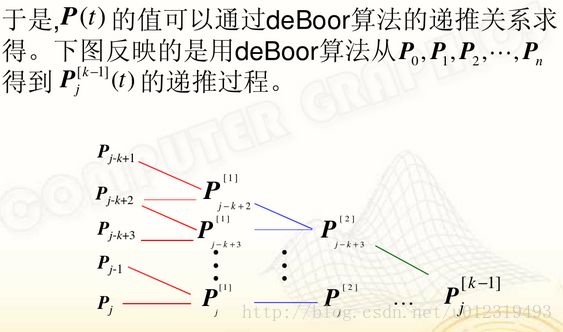
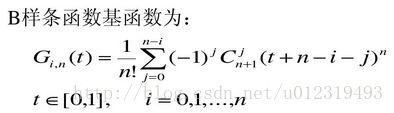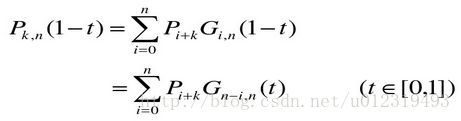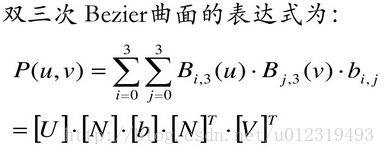Bezier、B样条曲线曲面

这里只列出核心，具体原理参看底部参考文献

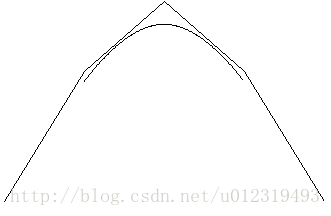
Bezier曲线

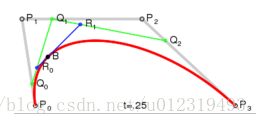
三次Bezier曲线

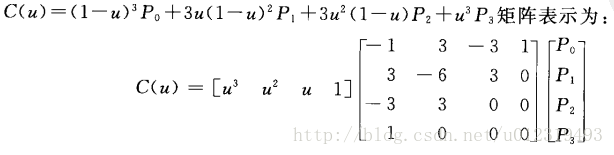
第一个控制点和最后一个控制点在曲线上：


两端点的切矢方向与控制多边形（特征多边形）的第一条和最后一条边一致：

Bezier曲线的递推性—de Casteljau算法

de Casteljau算法绘制Bezier曲线：

#define nctlPoints 5     //控制点数
#define nPoints 1000     //曲线上的点数

//求Bezier上的点
float bezierPoint(float P[], double t)
{
    float P1[nctlPoints];
    for(int j=0; jint n = nctlPoints - 1;
    for(int r=0; rfor(int i=0; i1.0 - t) * P1[i] + t * P1[i+1];
        }
    }
    return P1[0];
}

//Bezier曲线
void bezierLine(CDC *pdc)
{
    //控制点
    float Px[] = {320, 400, 480, 560, 640};
    float Py[] = {280, 120, 50,  120, 280};

    //控制多边形
    pdc->MoveTo(Px[0], Py[0]);
    for(int i=0; iLineTo(Px[i], Py[i]);

    //曲线
    pdc->MoveTo(Px[0], Py[0]);
    float delta = 1.0 / nPoints;
    double t = 0.0;
    for(i=0; ifloat x = bezierPoint(Px, t);
        float y = bezierPoint(Py, t);
        t += delta;
        pdc->LineTo(x, y);
    }
}

B样条曲线

均匀三次B样条曲线




起点和终点性质完全相同：

性质：

分量形式：

#define nctlPoints 5   //控制点数
#define nPoints 100    //每段曲线上的点数

//3次均匀B样条曲线
void BLineLine(CDC *pdc)
{
    //控制点
    float Px[] = {320, 400, 480, 560, 640};
    float Py[] = {280, 120, 50,  120, 280};

    //控制多边形
    pdc->MoveTo(Px[0], Py[0]);
    for(int i=0; iLineTo(Px[i], Py[i]);

    //曲线
    double dt = 1.0 / nPoints;
    for(int k=0; k3; k++)
    {
        double a0 = (Px[k] + 4 * Px[k+1] + Px[k+2]) / 6;
        double a1 = -(Px[k] - Px[k+2]) / 2;
        double a2 = (Px[k+2] - 2 * Px[k+1] + Px[k]) / 2;
        double a3 = -(Px[k] - 3 * Px[k+1] + 3 * Px[k+2] - Px[k+3]) / 6;
        double b0 = (Py[k] + 4 * Py[k+1] + Py[k+2]) / 6;
        double b1 = -(Py[k] - Py[k+2]) / 2;
        double b2 = (Py[k+2] - 2 * Py[k+1] + Py[k]) / 2;
        double b3 = -(Py[k] - 3 * Py[k+1] + 3 * Py[k+2] - Py[k+3]) / 6;
        for (i=0; idouble t = i * dt;
            double t2 = t * t;
            double t3 = t2 * t;

            double xa = a0 + a1 * t + a2 * t2 + a3 * t3;
            double ya = b0 + b1 * t + b2 * t2 + b3 * t3;
            if(i==0) 
                pdc->MoveTo(xa, ya);
            else  
                pdc->LineTo(xa, ya);
        }
    }
}

B样条曲线

三阶（2次）：

deboor算法（可使计算更加快捷）：

#define nctlPoints 5   //控制点数
#define nPoints 100    //每段曲线上的点数

//3次B样条曲线
void deboor(CDC *pdc)
{
    //控制点
    float Px[] = {320, 400, 480, 560, 640};
    float Py[] = {250, 120, 50,  120, 250};

    //控制多边形
    pdc->MoveTo(Px[0], Py[0]);
    for(int i=0; iLineTo(Px[i], Py[i]);

    //曲线
    float T[nctlPoints+4];           //结点矢量 
    for(i=0; i4; i++)
        T[i] = i;
    float pointsX[nctlPoints+3][4], pointsY[nctlPoints+3][4];  //曲线上的点
    bool first = true;
    for(i=3; ifloat delta = (T[i+1] - T[i]) / nPoints;
        for(float t=T[i]; t<=T[i+1]; t+=delta) 
        {
            for(int k=0; k<=3; k++) 
            {
                for(int j=i-3+k; j<=i; j++) 
                { 
                    if(k==0) 
                    {
                        pointsX[j][k] = Px[j]; 
                        pointsY[j][k] = Py[j];
                    }
                    else 
                    { 
                        float alpha = (t-T[j]) / (T[j+4-k]-T[j]); 
                        pointsX[j][k] = (1.0 - alpha) * pointsX[j-1][k-1] + alpha * pointsX[j][k-1]; 
                        pointsY[j][k] = (1.0 - alpha) * pointsY[j-1][k-1] + alpha * pointsY[j][k-1] ; 
                        if(j==i && k==3)
                        {
                            if(first)
                                pdc->MoveTo(pointsX[j][3], pointsY[j][3]);
                            else
                                pdc->LineTo(pointsX[j][3], pointsY[j][3]);
                            first = false;
                        }
                    }
                }
            }
        }
    }
}

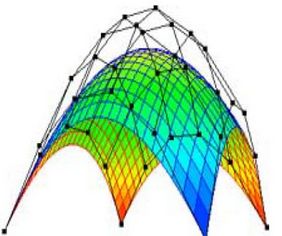
Bezier曲面

#include "vector"
#include "math.h"
using namespace std;

#define nPoints 100    //每段曲线上的点数

//矩阵乘法
vector< vector<float> > mul(vector< vector<float> > a, vector< vector<float> > b)
{
    int row = a.size();
    int rc = a[0].size();
    int col = b[0].size();
    vector< vector<float> > c(row, vector<float>(col));

    for(int i=0; ifor(int j=0; jfloat t = 0;
            for(int k=0; kreturn c;
}

//双3次Bezier曲面
void bezierArea(CDC *pdc)
{
    //控制点
    float Px[][4] = 
    {
        {100, 200, 300, 400},
        {110, 210, 300, 380},
        {130, 250, 330, 410},
        {150, 280, 360, 480}
    };
    float Py[][4] = 
    {
        {400, 300, 320, 400},
        {300, 280, 280, 320},
        {250, 200, 180, 200},
        {350, 250, 250, 280}
    };
    CPen newPen1(PS_SOLID, 4, RGB(0, 0, 255));
    CPen newPen2(PS_SOLID, 1, RGB(2550, 0, 0));

    //控制多边形

    pdc->SelectObject(&newPen1);
    int i, j;
    for(i=0; i<4; i++)
    {
        pdc->MoveTo(Px[i][0], Py[i][0]);
        for(j=0; j<4; j++)
            pdc->LineTo(Px[i][j], Py[i][j]);
    }
    for(i=0; i<4; i++)
    {
        pdc->MoveTo(Px[0][i], Py[0][i]);
        for(j=0; j<4; j++)
            pdc->LineTo(Px[j][i], Py[j][i]);
    }

    //曲面
    pdc->SelectObject(&newPen2);
    vector< vector<float> > U(1, vector<float>(4));
    vector< vector<float> > N(4, vector<float>(4));
    vector< vector<float> > bx(4, vector<float>(4));
    vector< vector<float> > by(4, vector<float>(4));
    vector< vector<float> > Nt(4, vector<float>(4));
    vector< vector<float> > Vt(4, vector<float>(1));
    N[0][0] = -1;  N[0][1] = 3;  N[0][2] = -3;  N[0][3] = 1;
    N[1][0] = 3;   N[1][1] = -6; N[1][2] = 3;   N[1][3] = 0;
    N[2][0] = -3;  N[2][1] = 3;  N[2][2] = 0;   N[2][3] = 0;
    N[3][0] = 1;   N[3][1] = 0;  N[3][2] = 0;   N[3][3] = 0;
    for(i=0; i<4; i++)
    {
        for(j=0; j<4; j++)
        {
            bx[i][j] = Px[i][j];
            by[i][j] = Py[i][j];
            Nt[j][i] = N[i][j];
        }
    }

    float delta = 1.0 / nPoints;
    for(float u=0; u<1; u+=delta)
    {
        for(i=0; i<4; i++)
            U[0][3-i] = pow(u, i);

        vector< vector<float> > tmp1 = mul(U, N);
        vector< vector<float> > tmp2x = mul(tmp1,  bx);
        vector< vector<float> > tmp3x = mul(tmp2x, Nt);
        vector< vector<float> > tmp2y = mul(tmp1,  by);
        vector< vector<float> > tmp3y = mul(tmp2y, Nt);
        pdc->MoveTo(tmp2x[0][0], tmp2y[0][0]);
        for(float v=0; v<1; v+=delta)
        {
            for(i=0; i<4; i++)
                Vt[3-i][0] = pow(v, i);
            vector< vector<float> > tmp4x = mul(tmp3x, Vt);
            vector< vector<float> > tmp4y = mul(tmp3y, Vt);
            pdc->LineTo(tmp4x[0][0], tmp4y[0][0]);
        }   
    }
}

B样条曲面

#include "vector"
#include "math.h"
using namespace std;

#define nPoints 100    //每段曲线上的点数

//矩阵乘法
vector< vector<float> > mul(vector< vector<float> > a, vector< vector<float> > b)
{
    int row = a.size();
    int rc = a[0].size();
    int col = b[0].size();
    vector< vector<float> > c(row, vector<float>(col));

    for(int i=0; ifor(int j=0; jfloat t = 0;
            for(int k=0; kreturn c;
}

//双3次B样条曲面
void BArea(CDC *pdc)
{
    //控制点
    float Px[][4] = 
    {
        {100, 200, 300, 400},
        {110, 210, 300, 380},
        {130, 250, 330, 410},
        {150, 280, 360, 480}
    };
    float Py[][4] = 
    {
        {400, 300, 320, 400},
        {300, 280, 280, 320},
        {250, 200, 180, 200},
        {350, 250, 250, 280}
    };
    CPen newPen1(PS_SOLID, 3, RGB(0, 0, 255));
    CPen newPen2(PS_SOLID, 1, RGB(2550, 0, 0));

    //控制多边形

    pdc->SelectObject(&newPen1);
    int i, j;
    for(i=0; i<4; i++)
    {
        pdc->MoveTo(Px[i][0], Py[i][0]);
        for(j=0; j<4; j++)
            pdc->LineTo(Px[i][j], Py[i][j]);
    }
    for(i=0; i<4; i++)
    {
        pdc->MoveTo(Px[0][i], Py[0][i]);
        for(j=0; j<4; j++)
            pdc->LineTo(Px[j][i], Py[j][i]);
    }

    //曲面
    pdc->SelectObject(&newPen2);
    vector< vector<float> > U(1, vector<float>(4));
    vector< vector<float> > N(4, vector<float>(4));
    vector< vector<float> > bx(4, vector<float>(4));
    vector< vector<float> > by(4, vector<float>(4));
    vector< vector<float> > Nt(4, vector<float>(4));
    vector< vector<float> > Vt(4, vector<float>(1));
    N[0][0] = -1;  N[0][1] = 3;  N[0][2] = -3;  N[0][3] = 1;
    N[1][0] = 3;   N[1][1] = -6; N[1][2] = 3;   N[1][3] = 0;
    N[2][0] = -3;  N[2][1] = 0;  N[2][2] = 3;   N[2][3] = 0;
    N[3][0] = 1;   N[3][1] = 4;  N[3][2] = 1;   N[3][3] = 0;
    for(i=0; i<4; i++)
    {
        for(j=0; j<4; j++)
        {
            bx[i][j] = Px[i][j];
            by[i][j] = Py[i][j];
            Nt[j][i] = N[i][j];
        }
    }

    float delta = 1.0 / nPoints;
    for(float u=0; u<1; u+=delta)
    {
        for(i=0; i<4; i++)
            U[0][3-i] = pow(u, i);

        vector< vector<float> > tmp1 = mul(U, N);
        vector< vector<float> > tmp2x = mul(tmp1,  bx);
        vector< vector<float> > tmp3x = mul(tmp2x, Nt);
        vector< vector<float> > tmp2y = mul(tmp1,  by);
        vector< vector<float> > tmp3y = mul(tmp2y, Nt);
        for(float v=0; v<1; v+=delta)
        {
            for(i=0; i<4; i++)
                Vt[3-i][0] = pow(v, i);
            vector< vector<float> > tmp4x = mul(tmp3x, Vt);
            vector< vector<float> > tmp4y = mul(tmp3y, Vt);
            if(v == 0)
                pdc->MoveTo(tmp4x[0][0]/36.0, tmp4y[0][0]/36.0);
            else
                pdc->LineTo(tmp4x[0][0]/36.0, tmp4y[0][0]/36.0);
        }   
    }
}

参考文献

和青芳. 计算机图形学原理及算法教程（Visual C++版）

Bezier曲线：
http://blog.csdn.net/joogle/article/details/7975118
https://www.zhihu.com/question/29565629
http://www.360doc.com/content/13/0830/14/110467_310949630.shtml

Bezier曲面：
http://blog.sina.com.cn/s/blog_73428e9a010171ta.html
http://www.docin.com/p-684461492.html

B样条曲线：
http://blog.csdn.net/app_12062011/article/details/50032629
http://wenku.baidu.com/link?url=jFzUqsDfvx76MREb_X5V7cbPHXypKEbG3jSnj9iL4IVYQdUh-c_f_1dPSGy1DZOJyEUQLnSjwcsr-zwKonStocgkHzZYS7huesl00WKDdBe
http://wenku.baidu.com/link?url=hj4sVeM6dGvgDFJEw_xRAMHdiYPrd2KEARfhPubnhz8PJC5QJ90xbjjGR-j-rC_8hYJBcgzpoe9MuNTzk0geLwmZc7Gyt5cA2hLqU-id7jW
http://blog.csdn.net/marcus2006/article/details/12419327

综合
http://wenku.baidu.com/link?url=w_BxPwYJkCP2qLXThvVDKV1UGdNPLIpCiZqFbAB63fjbBlMTLFurHQ3oJP7bJauOinAEEN3w5CoPvvbvLSZTrxDWB9cc7D3G38QGoN1Iwfq
http://wenku.baidu.com/link?url=Y_Owo5embqSmMPG-h4Nram-kX1CELRzekJNLig4z8a6EVpAop4TFLgTP043zaTzIE8RZ8qFXLsE07rkhEwBl6vwayMc8pT3wnCa6PFDrhr3