直方图与直方图绘制
From Wikipedia.org
In statistics, a histogram is a graphical display of tabulated frequencies, shown as bars. It shows what proportion of cases fall into each of several categories. The categories are usually specified as non-overlapping intervals of some variable. The categories (bars) must be adjacent. The intervals (or bands) should ideally be of the same size [1].
Histograms are used to plot density. The total area of a histogram always equals 1. If the length of the intervals on the x-axis are all 1, then a histogram is identical to a relative frequency plot.
The word histogram is derived from the Greek histos 'anything set upright' (as the masts of a ship, the bar of a loom, or the vertical bars of a histogram); and gramma 'drawing, record, writing'. The histogram is one of the seven basic tools of quality control, which also include the Pareto chart, check sheet, control chart, cause-and-effect diagram, flowchart, and scatter diagram. A generalization of the histogram is kernel smoothing techniques. This will construct a very smooth probability density function from the supplied data.
Activities and demonstrations
The SOCR resource pages contain a number of hands-on interactive activities demonstrating the concept of a histogram, histogram construction and manipulation using Java applets and charts.
[edit] Mathematical definition
In a more general mathematical sense, a histogram is a mapping mi that counts the number of observations that fall into various disjoint categories (known as bins), whereas the graph of a histogram is merely one way to represent a histogram. Thus, if we let n be the total number of observations and k be the total number of bins, the histogram mi meets the following conditions:
[edit] Cumulative histogram
A cumulative histogram is a mapping that counts the cumulative number of observations in all of the bins up to the specified bin. That is, the cumulative histogram Mi of a histogram mi is defined as:
[edit] Number of bins and width
There is no "best" number of bins, and different bin sizes can reveal different features of the data. Some theoreticians have attempted to determine an optimal number of bins, but these methods generally make strong assumptions about the shape of the distribution. You should always experiment with bin widths before choosing one (or more) that illustrate the salient features in your data.
The number of bins k can be calculated directly, or from a suggested bin width h:
The braces indicate the ceiling function.
- Sturges' formula [2]
-
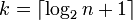 ,
,
which implicitly bases the bin sizes on the range of the data, and can perform poorly if n < 30.
where σ is the sample standard deviation.
which is based on the interquartile range.
[edit] Continuous data
The idea of a histogram can be generalized to continuous data. Let ![]() (see Lebesgue space), then the cumulative histogram operator H can be defined by:
(see Lebesgue space), then the cumulative histogram operator H can be defined by:
h(f)(y) is undefined if y is the value of a stationary point.
什么是直方图?
直方图(Histogram)也叫柱状图,是一种统计报告图,由一系列高度不等的纵向条纹表示数据分布的情况。
假设我们有一堆硬币,如下图所示,我们想知道一共有多少钱。
我们当然可以一枚一枚地数,但这样如果硬币多了可能会搞乱,因此我们需要先把硬币分类,然后分别统计每种硬币的数量。
把统计的结果图示出来,就成了直方图。下图的横向数轴标示出硬币的面额(Kind of Coins),纵向标示出硬币的数量(Number of Coins)。
图像的直方图
以灰度图为例,假设我们的图中一共只有0,1,2,3,4,5,6,7这8种灰度,0代表黑色,7代表白色,其它数字代表0~7之间不同深浅的灰度。
统计的结果如下,横轴标示灰度级别(0~7),纵轴标示每种灰度的数量。
Photoshop(PS)中的显示。
直方图统计数据
Photoshop CS提供了动态的直方图面板,CS之前的版本要通过图象>直方图来察看。
横轴标示亮度值(0~255),纵轴标示每种像素的数量。
像素(Pixels) - 图像的大小,图像的像素总数。[5*3=15]
色阶、数量、百分位这三项根据鼠标指针的位置来显示横坐标当前位置的统计数据。
色阶(Level) - 鼠标指针所在位置的亮度值,亮度值范围是0~255。[181]
数量(Count) - 鼠标指针所在位置的像素数量。[4]
百分位(Percentile) - 从最左边到鼠标指针位置的所有像素数量÷图像像素总数。[(1+2+1+2+3+4)/15 = 13/15 = 0.8667 = 86.67%]
当鼠标拖动,选中直方图的一段范围时,色阶、数量、百分位将显示选中范围的统计数据。
下面举个简单的例子来说明平均值、标准偏差、中间值。
例如图像A只有4个像素,亮度分别是200、50、100、200。
平均值(算术平均数,Mean,Average) - 图像的平均亮度值,高于128偏亮,低于128偏暗。平均值的算法是:图像的亮度总值÷图像像素总数。
平均值公式:
公式中,(读作X拨,X-bar)代表X的平均值,∑(读作西格玛,Sigma)代表总和,n代表X的总数。
[图像A的平均值 = (200+50+100+200)/4 = 550/4 = 137.5]
中间值(中值,中位数,Median) - 中间值是把图像所有像素的亮度值通过从从小到大排列后,位置处在中间的数。(如果有偶数个像素,就有两个位于中间的数,取前面的一个)
[图像A的中间值:亮度排序后50<=100<=200<=200,100和200是位于中间的,取前面的100作为中间值。]
标准偏差(标准差,Std Dev,Standard Deviation,Sample Variance) - 指图像所有像素的亮度值与平均值之间的偏离幅度。标准偏差越小,图像的亮度变化就越小,反之亮度变化就越大。
标准偏差公式:
图像A的标准偏差:(已知平均值 =137.5)
标准方差 S^2 = ((200-137.5)^2+(50-137.5)^2+(100-137.5)^2+(200-137.5)^2)/(4-1) = (62.5^2+(-87.5)^2+(-37.5)^2+62.52)/3 = (3906.25+7656.25+1406.25+3906.25)/3 = 16875/3 = 5625
标准偏差 S = 5625开平方 = 75
通道
Photoshop可以根据不同的通道来显示直方图,这些通道分别是RGB、红、绿、蓝、亮度和颜色,它们分别统计了不同的颜色数据。
下面举例来说明这些通道代表的含义。例如图像B只有3个像素,颜色值分别是RGB(0,10,20)、RGB(30,40,50)、RGB(60,70,80)。
红、绿、蓝通道 - 红色通道只统计颜色的R值,对于图像B只统计0、30、60这三个数字,然后根据这三个数字绘出直方图。绿色和蓝色通道也用相同的方法处理。
RGB通道 - 统计图像的所有RGB数据。对于图像B,要统计0、10、20、30、40、50、60、70、80这9个数字。
亮度通道 - 先用亮度公式Gray=0.3*R+0.59*G+0.11*B求出每个像素的亮度值,然后对这些亮度值进行统计。对于图像B,第一个像素的亮度值为 0.3*0+0.59*10+0.11*20=8.1,用同样的方法求出另两个像素的亮度值分别为38.1和68.1,然后四舍五入取整,对8、38、 68这三个数字进行统计。
[注] 有些软件用Gray=(R+G+B)/3作为亮度公式进行统计,例如GIMP。
颜色通道 - 把红、绿、蓝和RGB通道的统计数据绘制在同一幅图中。
高速缓存级别(Cache level)
为什么要用缓存(Cache)?
我们在处理一些超大的图片时,会因为像素数量过多而导致每一步操作都很慢,为了提高图片的显示与刷新速度,Photoshop利用图片的缩小版本来进行计算并显示。
当你载入一幅图片时,Photoshop会自动生成许多这幅图片的缩小版本放在临时文件中,这些缩小图就是高速缓存,其中有缩小到50%的、25%的、 12.5%的等等。当你把视图缩小时,比如缩小到25%,Photoshop就利用25%那张缓存小图的计算结果来更新视图。
缓存小图的不同缩小比例代表不同的缓存级别。缓存级别1为100%的原图,级别2为50%的小图,级别3为25%的小图,以此类推。
若要设定缓存级别,可以选择菜单编辑>预置>内存与图像高速缓存(Edit > Preferences > Memory and image cache)。Photoshop CS2的缓存级别默认值为6,适用于处理高质量的数码相机照片。
[注] Photoshop CS2之前的版本有一个“使用直方图高速缓存”(Use Cache for histogram)的选项,可以提高直方图的绘制速度,但会降低精确度。建议不要勾选此项,否则当你缩小视图时,Photoshop就会使用相应的缓存 小图来生成直方图。
缓存级别的算法
取上一级的四个相邻像素的平均值来获得一个像素,像素数是它上一级的1/4。
例如有张图片的大小是8*8,缓存级别2的大小为4*4,级别3为2*2,级别4为1*1。
下图是一张2*2像素的棋盘格图片,缓存级别2的灰度值取原图的平均值(0+255+255+0)/4=500/4=128。
直方图面板中的缓存级别
当图片较大时,为了提高直方图的刷新速度,Photoshop会自动选择适当的缓存级别来生成直方图。
现在来研究一下直方图面板中的缓存级别。新建一个2*2像素的图片,画成棋盘格图案,然后执行编辑>定义图案。
新建一个1000*1000像素的图片,灰度模式。
使用编辑>填充命令和前面定义的图案来填充这张图片。
这时看一下直方图面板,会发现右上角多了一个警告图标。这是缓存级别2的图片。通过直方图我们可以看出缓存级别2是张纯灰色的图片,灰度值128,像素数量250000,正好是原图的1/4。
单击那个警告图标,现在已经更新为原图的直方图。像素数量为1000*1000=1000000,有0和255两种灰度,平均值为255/2=127.50。这些都是原图的正确数据,正是我们所期望的。
对于一般的图像,为了提高速度而使用缓存生成直方图基本上是可行的,但要注意原图相邻像素的亮度变化越大,缓存小图造成的误差就越大。
直方图的Y轴范围
前面我们已经知道,Photoshop直方图的X轴标示亮度值,Y轴标示每种像素的数量。X轴的数值范围是0~255,现在来讨论一下Y轴的范围。
以bracket.bmp的蓝色通道为例,注意看下图中所显示的数据。
这幅图像的像素总数为19200。当鼠标光标移到直方图最左边(色阶为0)时,显示出数量的最大值684,这个最大值应该就是最长的一条竖线。当鼠标向右 移动到色阶2时,数量为526,但竖线仍是同样长度,这说明色阶0的竖线被Photoshop裁去了一部分。那么Photoshop是如何确定该裁去多少 呢?
我们可以给Y轴一个固定的范围,例如0~1120,这时的直方图显示如下。可以看出,最大值684以上的部分都是空白,而图形下部很纤细,看不清细节。
我们也可以把Y轴的范围缩小到0~135,这时图形被纵向拉长了,我们可以看出很多图形下部的细节,但图形的上部有太多被裁掉了。
比较常见的一种方法是把图形缩短或拉长到正好适合视图的大小,此时范围是0~684(最大值)。大多数软件都使用这种方法,Photoshop在一般情况下也是这样。
上面的方法有一个最大的缺陷就是如果有几条特别长的竖线的话,其它的竖线会变得很短而不利于我们观察它们的细节,所以Photoshop会把这些长竖线裁去一些。
Photoshop确定Y轴范围的原则是如果最大值超过像素总数的64分之一,那么就用像素总数÷64作为Y轴范围的上限,否则以最大值作为上限。
bracket.bmp的像素总数为19200,19200/64=300,因为最大值684>300,所以Y轴的范围是0~300。
直方图的算法
看到论坛上有人认为计算直方图开销最大的是标准偏差,还有人认为有必要取消标准偏差的显示项以提高速度。其实标准偏差的计算量并不大,就看你怎么去计算 了。前面讲过的一些算法的确会让人误以为计算这些数据时要对每个像素都进行加减乘除乘方等运算,所以我觉得有必要讨论一下直方图的具体计算过程。
要绘制直方图,首先要建立一个储存每种灰度数量的数据表(GrayTable),GrayTable是一个大小为256的数组。然后要对图像的每一个像素 进行统计,把每种灰度的像素数量记录到GrayTable中。这一步是必须的,不能偷工减料,这部分的计算量与像素的数量成正比,因此图像越大,计算的速 度就越慢。要想提高速度,唯一的方法就是使用缓存中的小图进行计算,但这样会降低精确度,不过对于实时更新的动态直方图来说,这么做还是很有必要的。
数据表GrayTable准备好了已后,平均值、中间值和标准偏差都可以利用GrayTable里的数据来计算,也就是说没必要再对每个像素进行计算了。无论图像有多大,GrayTable里都只存放256个数字,所以计算起来相当快。
举例来说,例如GrayTable中存放了以下的数据。
平均值 = (0*3 + 1*2 + 2*1 + 3*5 + 0 + 255*1) / (3+2+1+5+0+1) = 274/12 = 22.8
看到了吧,用乘法就行了,灰度值×数量再相加。标准偏差也是用类似的方法计算。GrayTable的灰度值是从小到大排列的,所以计算中间值也很方便。
对于动态直方图来说,也可以利用GrayTable来优化。有些时候,我们没有必要重新统计整幅图像的像素来更新直方图,只要把先前直方图的 GrayTable里的数据调换一下位置就行了,这种方法仅限于单幅图像单像素的处理(点运算)。例如做反色运算后,新的直方图其实就是把原来的直方图左 右翻转了一下。这样无论图像有多大,都可以做到精确的实时更新。
Photoshop图像菜单的功能几乎都可以使用这种优化,但Photoshop目前还没做到这一点,估计是怕麻烦吧。一些高画质数码照片处理软件可以考虑把这个功能加进去。
上文书转载自:灰鹿色彩笔记 http://hi.baidu.com/graydeer 感谢灰鹿同志超一流的教学水准!
Matlab中含有一个函数 Hist
HIST Histogram.
N = HIST(Y) bins the elements of Y into 10 equally spaced containers
and returns the number of elements in each container. If Y is a
matrix, HIST works down the columns.
N = HIST(Y,M), where M is a scalar, uses M bins.
N = HIST(Y,X), where X is a vector, returns the distribution of Y
among bins with centers specified by X. The first bin includes
data between -inf and the first center and the last bin
includes data between the last bin and inf. Note: Use HISTC if
it is more natural to specify bin edges instead.
[N,X] = HIST(...) also returns the position of the bin centers in X.
HIST(...) without output arguments produces a histogram bar plot of
the results. The bar edges on the first and last bins may extend to
cover the min and max of the data unless a matrix of data is supplied.
HIST(AX,...) plots into AX instead of GCA.


