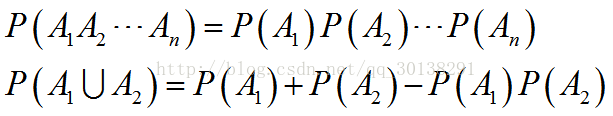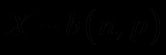概率与数理统计学习总结三--条件概率、全概率、贝叶斯、离散型随机变量
老师课堂总结,请勿转载
条件概率
设试验E的样本空间为S, A, B是事件, 要考虑在A已经发生的条件下B发生的概率, 这就是条件概率问题.
1. 定义: 设A, B是两个事件, 且P(A)>0, 称
为在事件A发生的条件下事件B发生的条件概率
条件概率满足三个条件
非负性:对于每一事件B有
规范性:对于必然事件S,有
可列可加性:设B1,B2,…是两两互不相容的事件,则
另外,对于任意两个事件
乘法定理
推广到多个事件的积事件情况
全概率公式与贝叶斯公式
样本空间划分
设S为实验E的样本空间,B1,B2,…Bn为E的一组事件. 若
则称B1,B2,…Bn为样本空间S的一个划分
设试验E的样本空间为S, A为E的事件, B1,B2,…Bn为样本空间S的一个划分, 且P(Bi)>0,i=1,…n,则成下式为全概率公式
贝叶斯(Bayes公式)
设试验E的样本空间为S, A为E的事件, B1,B2,…Bn为样本空间S的一个划分, 且P(A) >0, P(Bi)>0, i=1,…n, 则称下式为
特别在n=2情况下,全概率公式与贝叶斯公式可写为:
独立性
设A,B为两事件,如过满足P(AB)=P(A)P(B)则称事件A,B相互独立
若P(A)>0, P(B)>0,则A,B相互独立与A,B互不相容不能同时成立
若A,B相互独立,则下列各对事件也相互独立:
若三个事件A,B,C满足:
P(AB)=P(A)P(B)
P(AC)=P(A)P(C)
P(ABC)=P(A)P(B)P(C)
则称事件ABC相互独立
若事件A1,A2,…An相互独立,则其中任意k(2≤k≤n)个事件也是相互独立
若事件A1,A2,…An相互独立,则其中任意k(2≤k≤n)个事件换成它们各自对立的事件,所得到的n个事件也是相互独立若A,B相互独立,则
独立事件的乘法定理和加法定理
随机变量回顾
设随机试验的样本空间为S={e}. X=X(e)是定义在样本空间S上的实值单值函数.称X=X(e)为随机变量
离散型随机变量
连续型随机变量
离散型随机变量:
有些随机变量,它全部可能取到的值是有限个或可列无限多个,这种随机变量称为离散型随机变量
设离散型随机变量X所有可能取的值为xk(k=1,2,…),X取各个可能值的概率,即事件{X=xk}的概率, 为
P{X=xk}=pk, k=1,2,…
该式称为离散型变量X的分布律 (分布律也可用表格形式呈现,X的概率以一定的规律分布在各个可能值上,因此称为分布律)
由概率的定义,满足如下条件:
pk ≥ 0, k = 1, 2, …
(0-1)分布
设随机变量X可能取0与1两个值,它的分布律为
P{X=k}=p^k*(1-p)^(n-k),0
二项分布
设试验E只有两个可能结果:  则称E为伯努利试验. 设
则称E为伯努利试验. 设
将E独立重复进行n次, 则称这一串重复的独立试验为n重伯努利试验. 重复实值在每次试验中P(A)=p保持不变,独立实值各次试验结果互不影响。
X表示n重伯努利试验中事件A发生的次数,X是一个随机变量,由于各次试验相互独立,因此事件A在指定的k(1≤k≤n)次试验中发生,在其他(n-k)次试验中A不发生,得到n重伯努利试验的分布律
X服从参数为n,p的二项分布
n=1时伯努利分布变成了0-1分布