线性代数的本质（3）——映射、对角化、特征值与特征向量

这是我写的关于线性代数的第三篇文章，这些内容与前两篇文章的内容有很多的关联，如果不太了解行列式、线性变换的同学可以先看看我之前写的两篇文章，跳转链接如下：《线性代数的本质（1）——基底、向量、线性变换、逆阵、行列式》、《线性代数的本质（2）——线性相关/无关、秩、伴随矩阵、线性方程组、核、像》。
这里还是要强调两点：

1. 这是我个人的总结与理解，如果有错误的地方请理解，也麻烦指出我的错误，谢谢；
2. 这篇文章不是以应试为目的的，而是在于讲解线性代数的本质，如果是只想学会怎样计算的同学可以不用浪费时间了。

一、映射

如果对高中知识还有印象的同学一定记得高中数学讲过“单射、满射、双射”这些概念，线性代数中也是一样的，毕竟矩阵就是映射，而对角化的内容会用上映射的知识，所以我们这里先讨论映射。

在讨论映射前，先要提两个要点：

1. 对于相同的结果y，引起它的原因x是唯一的吗？
2. 无论什么样的结果y，都能找到导致它相应的原因x吗？

我们先来简单翻译下上面两个要点：

1. 在原空间中是否存在多个点，这些点经过线性变换后映射到相同的一个点上？
2. 原空间中的点经过线性变换后能否把目标空间的所有点覆盖完全？

然后根据以上的要点获得的结果翻译一下为：

1. 如果原空间只有一个点经过线性变换后映射到另外一个点上，那么是单射；如果有多个点映射到同一个点，那么不是单射；
2. 如果原空间的点经过线性变换后可以把目标空间全部覆盖，那么为满射，否则不是满射。

根据上面两个要点，我们来依次分析：既不是满射也不是单射、单射但不满射、满射但不单射、双射。

注：接下来的用图我会使用《程序员的数学：线性代数》P121页的图。

1. 既不是满射也不是单射

这里要注意一点，x1与x2是在同一个平面的点。

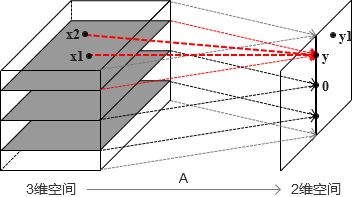
然后我们通过上面的要点来分析，首先这个线性变换是将三维空间变换到一个二维空间，但是压缩太厉害，在这个二维空间中只映射在了一条线上面，于是我们发现，有多个点映射到了同一个点上，比如x1和x2所在的空间映射到了y这一点；且原空间是三维，但是只映射到了这条线上，并没有覆盖完整个二维空间，比如y1就没有被覆盖到，所以这种情况属于“既不是满射也不是单射”。

我这边举一个代数的栗子方便大家更好地理解（不一定是正确的栗子，但是运算过程我保证正确）：

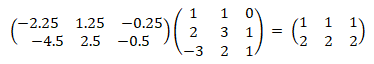
我们发现这个线性无关的方阵张成了一个三维空间（原空间），在矮矩阵的线性变换下，投影到了这个二维空间中，但是这个投影又是个线性相关的，也就是说其实是被压缩到了一维，但是它本身应该张成一个二维，所以这里既不是单射也不是满射。

2. 满射但不是单射

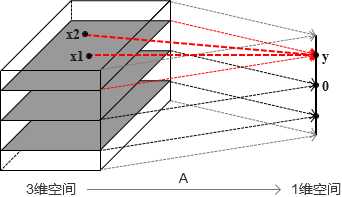
这个就特别单纯，从原空间直接映射到了一维上，完全覆盖了该空间，所以是满射，但是在目标空间的任意一点都无法还原为原空间（升维不易），或者说有多个点映射到了同一个点上，所以不是单射。

同样举个代数上的栗子：

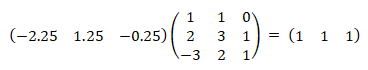
同样是上面这个线性无关的三维空间（原空间），在矮矩阵的线性变换下，投影到了这个一维空间中，这个是完全覆盖的（结果就是个x轴方向的一个单位向量上的所有点），所以这里既是满射但不是单射。

3. 单射但不是满射

像这种情况，原空间映射到目标空间每个点都是一一对应的，所以是单射，但是由于是从低维到高维的映射，那么肯定无法覆盖目标空间的每个点，所以不是满射。

还是一个栗子：

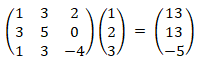
这里就是一个一维向量（1 2 3）^T在三维线性变换下的一个映射过程，虽然结果还是一维，但是过程是经历了一个三维的变换，也就对应上图只是在三维中有个直线的投影，而这里我们以结果来看，可以微妙的看成其实就是一个向量移动到了另外一个向量这里，所以是一一对应，也就是单射但不是满射。

4. 双射

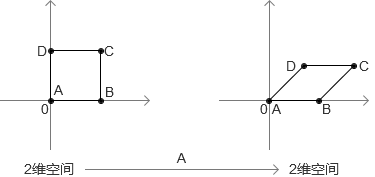
从上图就看得出来，变换前后的点都一一对应，且恰好覆盖完了目标空间，所以这里是双射，也可以理解为“没有升维以及降维的线性变换”。

善始善终，还是一个栗子：

这就是一个形如上面图示的一个线性变换，维度没有发生变化，目标空间被完全覆盖了，且点与点一一对应。

二、对角化

在我考研的时候对角化和特征值还有特征向量一般来说稳稳的是线代的大体，但是对角化究竟有什么用？特征值特征向量又是啥？这些都是我之前没考虑过的问题，所以这里来讨论一下这两个话题。

我们要首先明确一个公式：

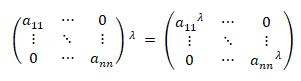
这个公式表达了，一个对角阵的λ次方等于对角阵里面每一项的λ次方，而实际作用是用在矩阵特征方程（也就是需要进行递推的方程）中，形如“x(t) = Ax(t - 1)”类型的特征方程，这样可以判断由这个矩阵特征方程表达的系统是发散的或者是收敛的。

因为x(t) = Ax(t - 1)，x(t - 1) = Ax(t - 2)…所以x(t) = A^tx(0)（x(0)不为0），那么从上面这个公式来看，A一定是个对角阵才方便进行敛散性的判断。

敛散性的判断如下：

1. A中的每一项的绝对值小于等于1 ，那么系统是收敛的，即|a₁₁| ≤ 1 && |a₂₂| ≤ 1 && … && |a_nn| ≤ 1。为何收敛，我们直接画个a^t的函数图就可以得出了，当t趋近于无穷时，|a|小于等于1的时候是趋近于0的；但是如果有任意一个|a|的绝对值大于1，那么整个系统就有发散的风险；
2. A中至少有一项绝对值大于1，那么系统是发散的，即|a₁₁| ＞ 1 || |a₂₂| ＞ 1 || … || |a_nn| ＞ 1。发散的图和上述一样，会发现当t趋近于无穷的时候，函数图像都要飞出坐标轴的感觉。

但是我们会发现两个严肃的问题：

1. 有的矩阵A不是对角阵，那么这种怎么判断敛散性？
2. 矩阵A能否可以通过初等变换变成对角阵？

我们就上面两个问题讨论。

1. 初等变换的不可行性

注：这一部分理解可能不够到位

我们先来明确整个公式：x(t) = Ax(t - 1)，这里x(t)与x(t - 1)是向量（一个系统的线性方程组），A是一个矩阵。

初等变换在纸上计算无非就是两行（两列）相加减，使得整个矩阵变为对角线上只有1或者0，其余地方全是0的变换，那么这其实也是一种线性变换，那么我们可以假设这个初等变换为CA（C为一个可逆阵），所以我们假设t为2，这时候如果进行初等变换，那么公式为：x(2) = (CA)x(1)。

由于矩阵乘法具有结合律，所以x(2)也等于C(Ax(1))，那么我们按照这样的思路一直递推下去，我们会发现其实x(t - 1)每一轮基本都是不一样的，那么要进行的初等变换的C其实每一轮也基本不一样，那么我们是无法通过初等变换进行归纳的。

2. 如何对角化

当初等变换前功尽弃后，我们就会考虑要如何把A变为对角阵的问题了，这就是对角化。

这里我先把对角化我个人的理解放在下面：

由于原系统的线性方程组的系数矩阵不一定是对角的，所以我们很难通过A^λ这种方式进行判断，所以需要另外一个系数矩阵是对角阵的线性方程组来表示我们的线性方程组，即将原系统通过线性变换变换为目标系统，在目标系统上判断系统的敛散性，之后再通过逆变换变换回原系统。

这里就要引入一个概念，名叫“基变换”。

2.1 基变换

基变换简单来说就是，我们通常取的基底（二维）是[1 0]^T和[0 1]^T，但是我们想使用另外一对基底（假设[1 1]^T和[-1 2]^T）来表达一个线性变换；或者将另外一组基底表达的线性变换转换为我们取的基底来表达。

也就是一种翻译工作，可以理解为同一个意思，我们用中文表达，老外用英文表达，要么我们把中文翻译为英文，要么我们把英文翻译为中文。

接下来我用一个栗子来从几何和代数的角度来讲解基变换：

前提条件如下（借用3B1B的栗子）：

我们的基向量i和j是[1 0]^T和[0 1]^T，另外一个基向量a和b为[2 1]^T和[-1 1]^T，我们的目标是有一条向量v[-1 2]^T是被a和b表达出来的，我们想将v逆时针旋转90度，再看看v变换为了啥。

我们结合上矩阵那一节讨论的，线性变换需要保证：

1. 原点不会移动；
2. 每个格子之间保持平行于等间距。

我们把上面的图翻译为中文就是如下：

1. 我们要把用a和b表达出来的这个向量v逆时针旋转90度；
2. 首先先把a和b表达的向量用i和j表达出来（这样方便我们理解），而用i和j表达a和b的矩阵np.mat(“2 -1; 1 1”)我们记为P，于是这里就是Pv；
3. 接着我们在i和j表达的情况下，逆时针旋转90度，逆时针旋转的线性变换为np.mat(“0 -1; 1 0”)，我们记为A，于是这里就变为了APv；
4. 最后我们发现，这是在我们的坐标系里面表达出来的内容，我们需要变回去a和b表达，所以这里取逆，就变为了最后的P^-1APv。

我们把上面说的P^-1AP记为∧，这个∧就代表了我们可以在a和b这个坐标系里面操纵任意的向量逆时针旋转90度，当我们改变A的时候，就改变了在a和b这个坐标系里面的线性变换方式。

2.2 对角化与基变换的关系

结合上面的基变换与对角化的理解，我们来做如下的分析：

首先我们设∧ = P^-1AP，这是暗示了数学上的转移作用，A代表我们想要的或者说所见的变换，P^-1和P代表转移作用（视角上的转换），∧和A代表的是同一种变换，只不过是从不同的基底的角度来看的。

回归到之前我们说的系统的问题上，整个系统的表达如下：

1. x(t) = Py(t)；
2. y(t) = P^-1x(t) = P^-1Ax(t - 1) = P^-1A(Py(t - 1)) = (P^-1AP)y(t - 1)

这里结合上我们之前说的东西，就是x(t)这个系统的系数矩阵无法对角化，所以用可对角化的y(t)表达，结合上上面的图示，就能够理解这两个公式了。

但是我们这里都是在以上帝视角来看的这个问题，就是我们总能找到这么一个可以变为对角阵的系统，但是如果我们不知道（大概率不会知道），要怎么样才找得到呢？就要引出特征值与特征向量了。

三、特征值与特征向量

我们的目标是有这么一个对角阵∧ = P^-1AP，任务就是找到对角化所需要的P，于是我们将P拆分成列向量的集合（p₁, …, p_n），设所求的对角阵如下：

在上面的式子中，左乘P，得到下式：

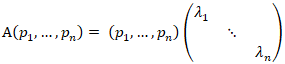
我们把左右分别相乘进去，再把每一列提出来看，就会发现如下的式子：

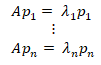
是不是这里就发现，这就是AP = λP，P ≠ 0，λ为特征值，P为特征向量。

3B1B在视频中讲到，由于P^-1AP中P是特征向量，所以这里叫特征基变换，使用特征基变换，那么P^-1AP必然是对角的，且对角元素为特征值，而为什么如此是因为它所处的坐标系的基向量在变换中只进行了缩放。
至于这里为什么对角化后得到的对角阵就是特征值构成的，以及为什么P就是特征向量，我还没有查到一个让我满意的答案，甚至包括3B1B说的话我也没能完全理解，如果后面看到了就再做补充。

1. 几何意义

特征向量的几何意义在于：空间进行变换，总会有那么一些直线不会改变他们的空间（直线），只会改变方向和大小，即经过变换后仍存留在它们张成的空间（直线）中的向量。而特征值就是特征向量变化的大小。

这句话有点拗口，但是我们用个例子来讲解：

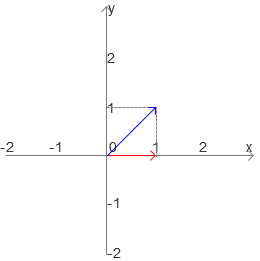
我们会发现，这个空间在np.mat(“1 1; 0 1”)这个变换下，x轴上的所有点都不会发生任何改变，所以这就是特征向量，而改变量为1，所以特征值为1。（具体动画可以看3B1B的视频）。

2. 运算

先上个公式：

这里I是单位阵，可以省略。

由于p是特征向量，非零的，所以对于整个等式来说，就必须使得A - λI = 0，根据零空间、行列式以及上面才提到的单射情况来看，这肯定是被压缩了空间的情况（因为要乘以一个非零向量为零，那么必须保证这个变换会导致空间被压缩到零空间），所以det(A - λI) = 0，也就是如下：

这里是假定A = np.mat(“a c; b d”)。

接着我们通过解行列式，得到(a - λ)(d - λ) - bc，从而解出来特征值。

小tip：如果特征值在实数空间没有值，那么通常来讲是进行了旋转，比如np.mat(“0 1; -1 0”)，特征值为±i。

解出特征值后，我们将特征值带回原方程中，比如：

那么说明二四象限角平分线就是特征值为2的特征向量，经过该线性变换后，这条直线上的所有点距离原点的距离都扩大了2倍，但是仍然在这条角平分线上。而这个这个特征向量在这个线性变换的作用下，会被压缩到零空间中。

小tip：会存在单一特征值，但是多个特征向量的情况，比如np.mat(“2 0; 0 2”)，说明了该空间中的每个向量都被拉伸了2倍，但是仅仅只拉伸了2倍。

四、参考

[1]3Blue1Brown.【官方双语/合集】线性代数的本质 - 系列合集[EB/OL].https://www.bilibili.com/video/BV1ys411472E,2016-10-18.
[2][日]平冈和幸,堀玄.程序员的数学3线性代数[M].人民邮电出版社:北京,2016.3:197.