《视觉SLAM十四讲》学习笔记:第4讲 李群与李代数
《视觉SLAM十四讲》学习笔记:第4讲 李群与李代数
前言:本学习笔记将记录《视觉SLAM十四将》中一些重要的知识点,并对书中一些比较难的知识点添加上一些笔者个人的理解,以供笔者本人复习并与各位同学一起交流学习。本笔记结构将与原书结构一致,如果某一目录下面没有任何笔记,则代表笔者认为该小节内容相对来说没有过多重点知识。
本讲主要解决问题
理论:
1.理解李群与李代数的概念,掌握 S O ( 3 ) , S E ( 3 ) SO(3),SE(3) SO(3),SE(3) 与对应李代数的表示方式
2. 理解 BCH 近似的意义。
3. 学会在李代数上的扰动模型。
实践:
1.使用 Sophus 对李代数进行运算。
本章意义:由于在SLAM中位姿是未知的,因此需要解决什么样的相机位姿最符合当前观测数据这个问题,其中一个典型的方式就是把它构建成一个优化问题,求解最优的 R , t R,t R,t,使得误差最小化。但是,如果直接将旋转矩阵/变换作为优化变量时,会引入额外的约束(旋转矩阵/变换本身带有约束,即旋转部分正交且行列式为1),因此会给优化带来许多麻烦。而通过李群——李代数间的转换关系,把位姿估计变成无约束的优化问题,简化求解方式。
4.1 李群李代数基础
4.1.1 群
1.群的定义,群是一种集合加上一种运算的代数结构。将集合记作 A A A,运算记作 ⋅ · ⋅,那么群可以记作 G = ( A , ⋅ ) G=(A,·) G=(A,⋅)。群要求这个运算满足以下几个条件:

可以验证,旋转矩阵集合和矩阵乘法构成群,同样变换矩阵和矩阵乘法也构成群。
2.李群:李群是指具有连续(光滑)性质的群。本章重点关注李群 S O ( 3 ) SO(3) SO(3)和 S E ( 3 ) SE(3) SE(3)。
4.1.2 重新排版说明
本章第一节剩余部分与本章第二节排版较原书略有不同,因此,可能会出现一些奇奇怪怪的节名
但是此处,我们首先需要明确,本章最终想要获得的,是典型的李群 S O ( 3 ) SO(3) SO(3), S E ( 3 ) SE(3) SE(3)分别和李代数 s o ( 3 ) so(3) so(3), s e ( 3 ) se(3) se(3)相互之间的转换关系
4.1.3 李代数的定义
每个李群都有与之对应的李代数。李代数描述了李群的局部性质(至于)。通用的李代数的定义如下:
李代数有一个集合 V V V,一个数域 F F F和一个二元运算[,]组成。如果它们满足以下几条性质,称 ( V , F , [ , ] ) (V,F,[,]) (V,F,[,])为一个李代数,记作 g g g。
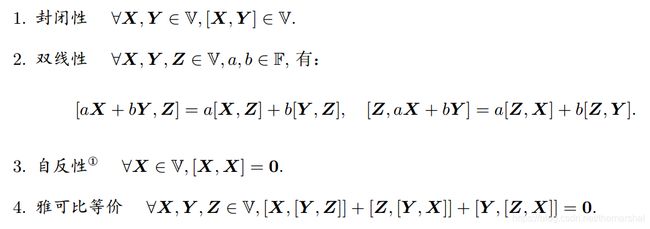
4.1.3 李代数so(3)
定义李代数 s o ( 3 ) so(3) so(3):

其对应的李括号为:

可以推导,李代数 s o ( 3 ) so(3) so(3)与 S O ( 3 ) SO(3) SO(3)的关系由指数映射给定:

其中, ϕ \phi ϕ满足:

推导过程如下:
对于任意旋转矩阵 R ∈ S O ( 3 ) R\in SO(3) R∈SO(3),有:

若认为 R R R会随时间连续地变化,比如相机的旋转,那么有:
![]()
等式两边对时间求导,得到:
![]()
整理得到:
![]()
因此,可以看出 R ˙ ( t ) R ( t ) T \dot{R}(t)R(t)^T R˙(t)R(t)T是一个反对称矩阵。
这里给出一个符号 ∨ \lor ∨该符号表示将反对称矩阵变为向量:

由于 R ˙ ( t ) R ( t ) T \dot{R}(t)R(t)^T R˙(t)R(t)T是一个反对称矩阵,可以找到一个三维向量 ϕ ( t ) ∈ R 3 \phi(t)\in R^3 ϕ(t)∈R3与之对应,于是有:

等式两边右乘 R ( t ) R(t) R(t),有:
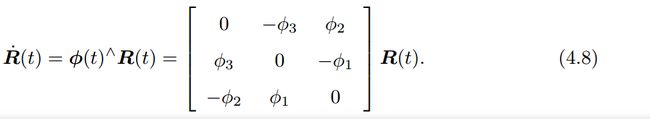
可以看到,每对旋转矩阵求一次导数,只需左乘一个 ϕ ( t ) ∧ \phi(t)^{\land} ϕ(t)∧矩阵即可。( ϕ ( t ) ∧ \phi(t)^{\land} ϕ(t)∧是和旋转矩阵有关的,而不是说上式的二阶导就是再加一个一模一样的 ϕ ( t ) ∧ \phi(t)^{\land} ϕ(t)∧)。
假设 t 0 t_0 t0等于0,并设此时旋转矩阵为 R ( 0 ) = I R(0)=I R(0)=I,将 R ( t ) R(t) R(t)在0附近进行一阶泰勒展开:
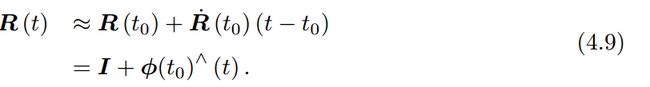
根据上式可以发现,在 t 0 t_0 t0附近,设 ϕ \phi ϕ保持为常数 ϕ ( t 0 ) = ϕ 0 \phi(t_0)=\phi_0 ϕ(t0)=ϕ0。那么有:
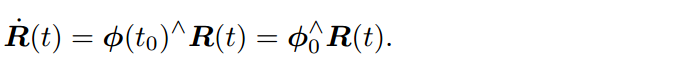
知道初始值 R ( 0 ) = I R(0)=I R(0)=I,求解上面的微分方程,得到:

(上面的推导由作者给出,个人感觉是有些奇怪的,其一,根据后面的结果, ϕ 0 ∧ \phi_0^{\land} ϕ0∧应该会随t变化,其二,罗德里格斯公式并没有 R ( 0 ) = I R(0)=I R(0)=I这样的限制,笔者数学并没有学到这个部分,目前还在查询相关资料,欢迎各位明白这个公式推导的大佬解释)。
4.1.4 李代数se(3)
s e ( 3 ) se(3) se(3)位于 R 6 R^6 R6空间中:

我们把每个 s e ( 3 ) se(3) se(3)元素记作 ξ \xi ξ,它是一个六维向量。前三维为平移,记作 ρ \rho ρ;后三维为旋转,记作 ϕ \phi ϕ,实质上是 s o ( 3 ) 元 素 so(3)元素 so(3)元素。同时,此处符号 ∧ \land ∧将一个六维向量转换成思维矩阵,但这里不再表示反对称。
李括号定义如下:

4.2 指数与对数映射
4.2.1 SO(3)上的指数映射
指数映射定义如图所示(在收敛的情况下有结果):

同样地,对 s o ( 3 ) so(3) so(3)中任意一元素 ϕ \phi ϕ,可以定义它的指数映射:

下面进一步进行推导,由于 ϕ \phi ϕ是三维向量,可以定义它的模长和方向,分别记作 θ \theta θ和 a ⃗ \vec{a} a,于是有 ϕ ⃗ = θ a ⃗ \vec{\phi}=\theta\vec{a} ϕ=θa。这里 a a a是一个长度为1的方向向量。首先,对于 a ∧ a^{\land} a∧,有以下两条性质:

利用这两个性质,可以把指数映射写成:
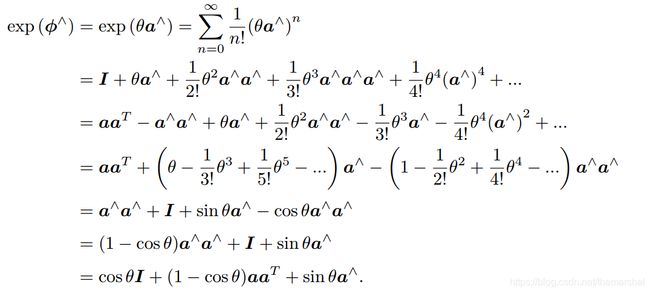
最终推导得到的公式即为罗德里格斯公式:
![]()
这也说明 s o ( 3 ) so(3) so(3)实际上就是由所谓的旋转向量组成的空间,而指数映射即罗德里格斯公式。通过它们,把 s o ( 3 ) so(3) so(3)中任意一个向量对应到了一个位于 S O ( 3 ) SO(3) SO(3)中的旋转矩阵。反之,如果定义对数映射,也能把 S O ( 3 ) SO(3) SO(3)中的元素对应到 s o ( 3 ) so(3) so(3)中:
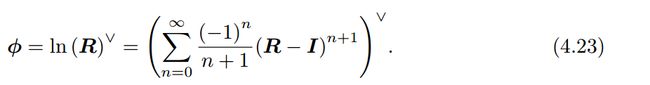
但是,通常不用泰勒展开去计算对数映射,而是用第3讲中的方法利用迹的方法分别求解转角和转轴。
指数映射只是一个满射,可能存在多个 s o ( 3 ) so(3) so(3)中的元素,对应到同一个 S O ( 3 ) SO(3) SO(3)。但是,如果把旋转角度固定在正负 π \pi π之间,那么李群和李代数元素是一一对应的。
由此,可以发现旋转矩阵的导数可以由旋转向量指定,指导着如何在旋转矩阵中进行微积分运算。
4.2.2 SE(3)上的指数映射
s e ( 3 ) 上 的 指 数 映 射 形 式 如 下 : se(3)上的指数映射形式如下: se(3)上的指数映射形式如下:
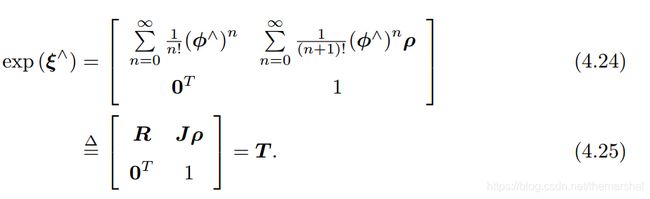
推导如同 s o ( 3 ) so(3) so(3)。从结果上看, ξ \xi ξ的指数映射左上角的 R R R是 S O ( 3 ) SO(3) SO(3)中的元素,与 s e ( 3 ) se(3) se(3)当中的旋转部分 ϕ \phi ϕ,右上角的 J J J则整理为(设 ϕ ⃗ = θ a ⃗ \vec{\phi}=\theta\vec{a} ϕ=θa):
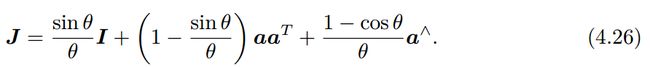
由此可见,平移部分经过指数映射之后,发生了一次以 J J J为系数矩阵的线性变换。
同样的,也可以推得对数映射,但是通过这个方式得到:
![]()
由于 J J J可以由 ϕ \phi ϕ得到,所以这里的 ρ \rho ρ亦可由此线性方程解得。
由此,李群、李代数的相互的转换关系已经完全结束。
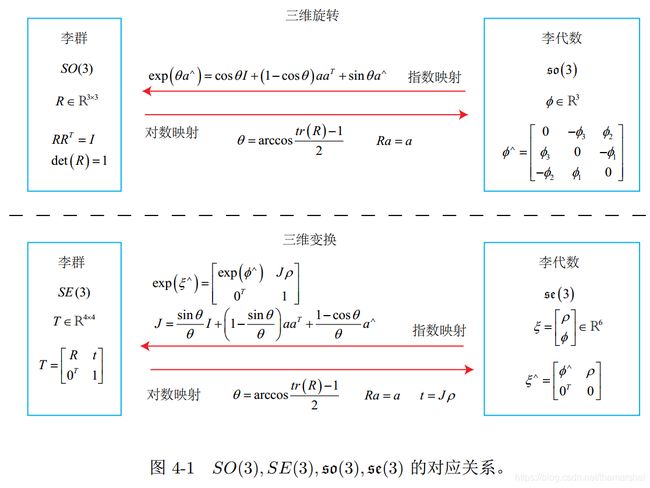
4.3 李代数求导与扰动模型
4.3.1 BCH公式与近似形式
两个李代数指数映射乘积的完整形式,由Baker-Campbell-Hausdorff 公式(BCH公式)给出。其展开式的前几项如下:
![]()
其中 [ ] [] []为李括号。
特别地,考虑 S O ( 3 ) SO(3) SO(3)上的李代数 l n ( e x p ( ϕ 1 ∧ ) e x p ( ϕ 2 ∧ ) ∨ ln(exp(\phi_1^{\land})exp(\phi_2^{\land})^{\lor} ln(exp(ϕ1∧)exp(ϕ2∧)∨,当 ϕ 1 \phi_1 ϕ1或 ϕ 2 \phi_2 ϕ2为小量时,小量二次以上的项都可以被忽略掉。此时, B C H BCH BCH拥有线性近似表达:
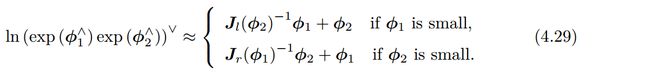
其中 J l ( ϕ 2 ) J_l(\phi_2) Jl(ϕ2)实际上代表了由 ϕ 2 \phi_2 ϕ2张成的左乘 B C H BCH BCH近似雅可比阵,实际上也就是:
![]()
它的逆为:
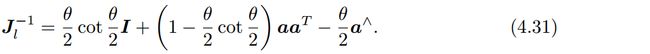
而右乘雅可比仅需要对自变量取负号即可:

下面阐述 B C H BCH BCH近似的意义:
假设对某个旋转 R R R,对应的李代数为 ϕ \phi ϕ。给它左乘一个对应的李代数为 Δ ϕ \Delta\phi Δϕ的微小旋转 Δ R \Delta R ΔR,那么,根据 B C H BCH BCH近似,可以得到:
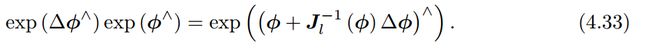
反之,如果在李代数上进行加法,让一个 ϕ \phi ϕ加上 Δ ϕ \Delta\phi Δϕ,那么可以近似为李群上带左右雅可比的乘法:
![]()
同样,对于 S E ( 3 ) SE(3) SE(3),也有类似的 B C H BCH BCH近似公式:
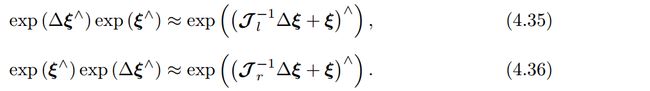
但是这里的 J l J_l Jl形式比较复杂,但基本不会用到其实际形式,这里略去。
4.3.2 SO(3)李代数上的求导
李代数求导问题的引出:
在SLAM中,我们要估计一个相机的位置和姿态,该位姿是由 S O ( 3 ) SO(3) SO(3)上的旋转矩阵或 S E ( 3 ) SE(3) SE(3)上的变换矩阵描述的。假设在某个时刻,机器人的位姿为 T T T,它观察到了一个世界坐标位于 p p p的点,产生了一个观测数据 z z z。那么,由坐标变换关系得:
![]()
这里 w w w是观测噪声。
由于观测噪声 w w w的存在, z z z往往不可能精确地满足 z = T p z=Tp z=Tp的关系,因此会计算理想的观测与实际数据的误差:

假设一共有 N N N个这样的路标点和观测,于是就有 N N N个上式。那么,对该机器人位姿的估计,相当于是寻找一个最优的 T T T,使得整体误差最小化:
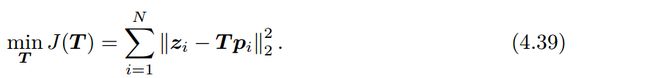
而求解这个问题,就需要计算目标函数 J J J关于变换矩阵 T T T的导数。
注意:这里重点要说的是, 我们经常会构建与位姿有关的函数,然后讨论该函数关于位姿的导数,以调整当前的估计值。然而, S O ( 3 ) SO(3) SO(3), S E ( 3 ) SE(3) SE(3) 上并没有良好定义的加法,它们只是群。如果我们把 T T T 当成一个普通矩阵来处理优化,那就必须对它加以约束。而从李代数角度来说,由于李代数由向量组成,具有良好的加法运算。因此,使用李代数解决求导问题的思路分为两种:
1.用李代数表示姿态,然后对根据李代数加法来对李代数求导。
2.对李群左乘或右乘微小扰动。然后对该扰动求导,称为左扰动和右扰动模型。(注意,扰动模型下的求导定义和数学上的微分定义不太一样。)
4.3.3 李代数求导
首先,考虑 S O ( 3 ) SO(3) SO(3)上的情况。假设我们对一个空间点 p p p进行了旋转,得到了 R p Rp Rp。现在,要计算旋转之后点的坐标相对于旋转的导数,记为(这里只是作为一个记号,其并不符合微分的数学含义):

由于 S O ( 3 ) SO(3) SO(3)没有加法,所以该导数无法按照导数的定义进行计算。设 R R R对应的李代数为 ϕ \phi ϕ,转而计算:

根据导数的定义,有:
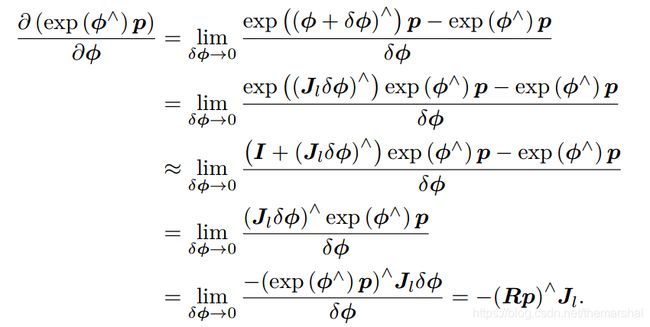
第二行的近似为 B C H BCH BCH线性近似,第三行为泰勒展开舍去高阶项后近似,第四行至第五行将反对称符号看作叉积,交换之后变号。于是,我们推导了旋转后的点相对于李代数的导数:

不过,由于这里仍然含有形式较为复杂的 J l J_l Jl,因此一般会用扰动模型。
4.3.4 扰动模型(左乘)
另一种求导方式,是对 R R R进行一次扰动 Δ R \Delta R ΔR,这个扰动可以乘在右边,最后结果会有一点儿微小的差异,以左扰动为例。(一定记住,这里的微分应该按照数学上的概念去理解,就是上面有一个微小变换,下面也有一个微小变换。而别用数学上面的定义来理解)。设左扰动 Δ R \Delta R ΔR对应的李代数为 φ \varphi φ。然后,对 φ \varphi φ求导,即:
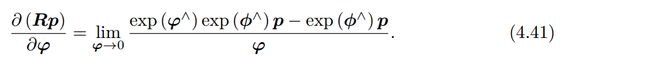
由此式得到:

可见,扰动模型相比于直接对李代数求导,省去了一个雅可比 J l J_l Jl的计算。因此扰动模型更为实用。
4.3.5 SE(3)上的李代数求导
仍然利用扰动模型,假如某空间点 p p p经过一次变换 T T T(对应李代数为 ξ \xi ξ),得到 T p Tp Tp。现在,给 T T T左乘一个扰动, Δ T = e x p ( δ ξ ∧ ) \Delta T = exp(\delta\xi^{\land}) ΔT=exp(δξ∧),设扰动项的李代数为 δ ξ = [ δ ρ , δ ϕ ] T \delta\xi=[\delta\rho,\delta\phi]^T δξ=[δρ,δϕ]T,那么:

最后的结果定义成一个算符 ⊙ \odot ⊙,它把一个 4 × 6 4 \times 6 4×6的矩阵。
4.4 实践: Sophus
直接make这个库会出现报错,根据报错信息,解决方法参考博客:
https://blog.csdn.net/shanpenghui/article/details/104297120
同时, i n c l u d e include include的文件需要改成:

否则会出现报错。
4.5 相似变换群与李代数
在单目SLAM中使用 S E ( 3 ) SE(3) SE(3)表示位姿,那么由于尺度不确定性与尺度飘逸,整个SLAM过程中的尺度会发生变化,这在 S E ( 3 ) SE(3) SE(3)中未能体现出来。因此,在单目情况下一般会显式地把尺度因子表达出来。用数学语言来说,对于位于空间的点 p p p,在相机坐标系下要经过一个相似变换,而非欧氏变换:

在相似变换中,我们把尺度 s s s表达了出来。它同时作用在 p p p的三个坐标之上,对 p p p进行了一次缩放。相似变换亦对矩阵乘法构成群,称为相似变换群 S i m ( 3 ) Sim(3) Sim(3):
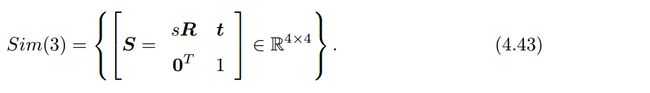
同样地, S i m ( 3 ) Sim(3) Sim(3)也有对应的李代数、指数映射、对数映射等等。李代数 s i m ( 3 ) sim(3) sim(3)元素是一个其为向量,它的前六维与 s e ( 3 ) se(3) se(3)相同,最后多了一项 σ \sigma σ。
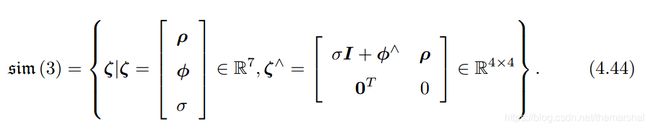
关联 S i m ( 3 ) Sim(3) Sim(3)和 s i m ( 3 ) sim(3) sim(3)的仍是指数映射和对数映射。指数映射为:

其中 J S J_S JS形式为:
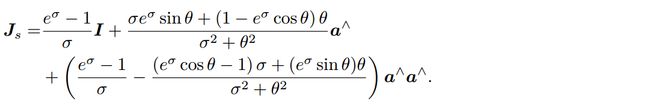
通过指数映射,我们能够找到李代数与李群的关系。对于尺度因子,可以看到李群中的 s s s即为李代数中 σ \sigma σ的指数函数。
同样的, S i m ( 3 ) Sim(3) Sim(3)的 B C H BCH BCH近似与 S E ( 3 ) SE(3) SE(3)是类似的,也存在微分模型和扰动模型两种方式,而扰动模型较为简单。设给予 S p Sp Sp左侧一个小扰动,并求 S p Sp Sp对于扰动的导数。因为 S p Sp Sp四维的齐次坐标, ζ \zeta ζ是七维向量,该导数应该是 4 × 7 4 \times 7 4×7的雅可比,记 S p Sp Sp的前三维组成向量 q q q,那么:
