使用MATLAB和ANSYS对四杆桁架结构进行有限元分析

问题的描述

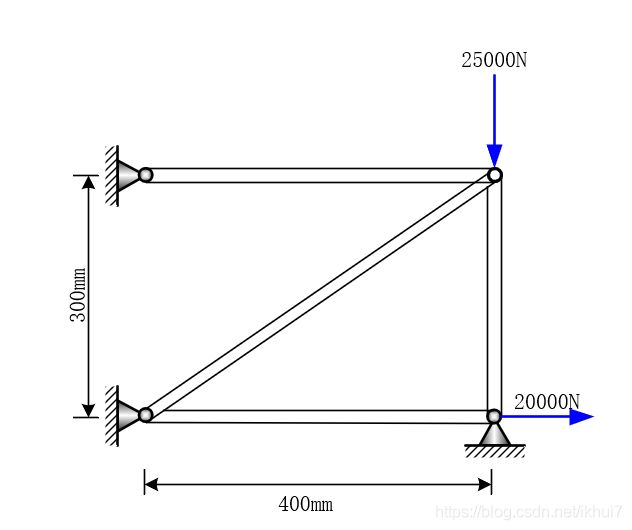
如图所示的结构，各杆的弹性模量和横截面积都为 E=2.96x10⁵ N/mm² ，A=100mm² ，试求解该结构的结点位移、单元应力及支座反力。

问题的分析

有限元分析过程：
（1）对结构进行离散化并编号；
（2）计算各单元的刚度矩阵；
（3）建立整体刚度方程；
（4）处理边界条件及求解刚度方程；
（5）计算支座反力；
（6）计算各单元应力。

利用MATLAB进行求解

1、结构离散化处理并编号，如下图：

2、计算各单元的刚度矩阵

clear
clc
% 参数初始化设置
E =2.95e11;  A = 0.0001;
x1 = 0;     y1 = 0;
x2 = 0.4;   y2 = 0;
x3 = 0.4;   y3 = 0.3;
x4 = 0;     y4 = 0.3;
alpha1 = 0; alpha2 = 90;
alpha3 = atan(0.75*180/pi);
% 计算单元刚度矩阵（SI单位）
k1 = Bar2D2Node_Stiffness(E, A, x1, y1, x2, y2, alpha1);
k2 = Bar2D2Node_Stiffness(E, A, x2, y2, x3, y3, alpha2);
k3 = Bar2D2Node_Stiffness(E, A, x1, y1, x3, y3, alpha3);
k4 = Bar2D2Node_Stiffness(E, A, x4, y4, x3, y3, alpha1);

3、建立整体刚度矩阵

% 建立整体刚度矩阵
KK = zeros(8,8);
KK = Bar2D2Node_Assembly(KK, k1, 1, 2);
KK = Bar2D2Node_Assembly(KK, k2, 2, 3);
KK = Bar2D2Node_Assembly(KK, k3, 1, 3);
KK = Bar2D2Node_Assembly(KK, k4, 4, 3);

4、处理边界条件与求解刚度方程

该结构的节点位移为：

q = ( u ₁ , v ₁ , u ₂ , v ₂ , u ₃ , v ₃ , u ₄ , v ₄) ^T

节点力为：

F = ( F _x1 , F _y1 , 2 x 10 ⁴ , F _y2 , 0 -2.5 x 10 ⁴ , F _x4 , F _y4 ) ^T

在边界条件和节点力的处理上，还需要人为地找出。由上图，我们可以看出，节点1的位移 u₁ = 0，v₁ = 0 ，节点2的位移v₂ = 0 ，节点4的位移 u₄ = 0，v₄ = 0 。施加的节点荷载 F_x2 = 2 x 10⁴ N ，F_x3 = -2.5 x 10⁴ N 。

% 计算结点位移
k = KK([3, 5, 6], [3, 5, 6]);
p = [20000; 0; -25000];
u = k\p;

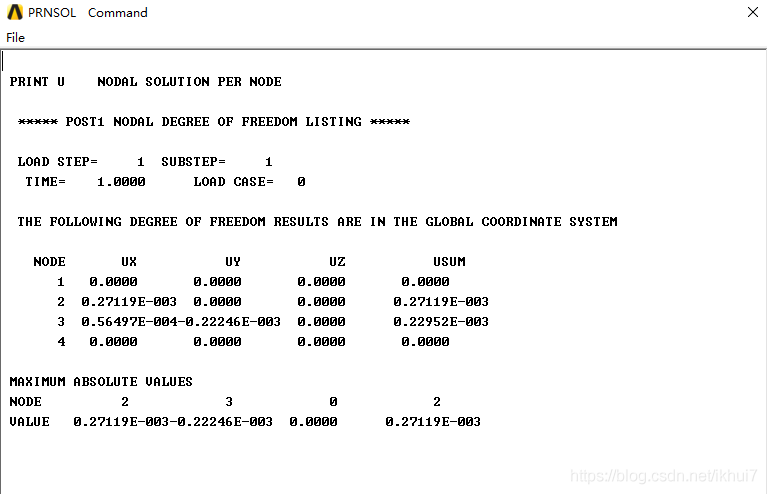
所有节点位移为：

q = ( u ₁ , v ₁ , u ₂ , v ₂ , u ₃ , v ₃ , u ₄ , v ₄) ^T =( 0 , 0 , 0.2712 , 0, 0.0565 , -0.2225 , 0, 0) ^T

5、计算支座反力

将整体位移列阵 q （采用SI单位）带入到整体刚度方程，即可计算出所有节点力P：

% 计算支座反力
q = [0 0 0.0002712 0 0.0000565 -0.0002225 0 0]';
P = KK*q;

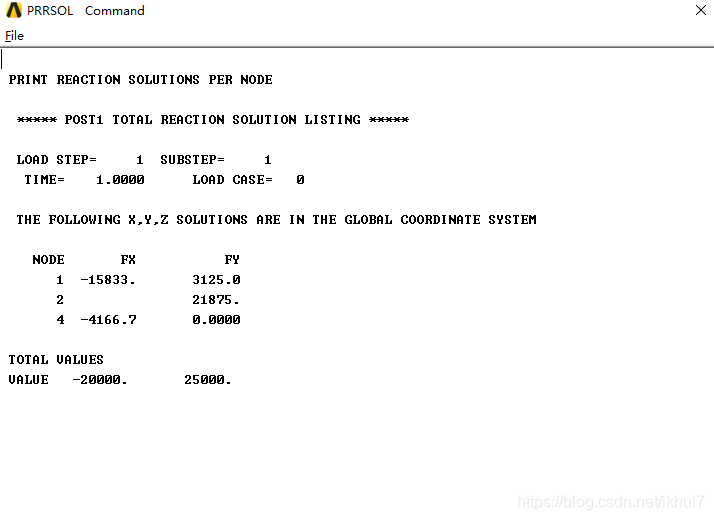
支座反力为：

P = ( P _x1 , P _y1 , P _y2 , P _x4 , P _y4 ) ^T =（-15833 , 3126 , 21879 , -4167 , 0） ^T

6、计算各单元应力

从整体位移列阵中提取各单元的位移列阵，然后计算单元应力。

% 计算单元应力
u1 = [q(1);q(2);q(3);q(4)];
stress1 = Bar2D2Node_Stress(E, x1, y1, x2, y2, alpha1, u1);

u2 = [q(3);q(4);q(5);q(6)];
stress2 = Bar2D2Node_Stress(E, x2, y2, x3, y3, alpha2, u2);

u3 = [q(1);q(2);q(5);q(6)];
stress3 = Bar2D2Node_Stress(E, x1, y1, x3, y3, alpha3, u3);

u4 = [q(7);q(8);q(5);q(6)];
stress4 = Bar2D2Node_Stress(E, x4, y4, x3, y3, alpha1, u4);

因此，单元1的应力为2.0001 x 10⁸ Pa，单元2的应力为-2.1879 x 10⁸ Pa，单元3的应力为-5.2097 x 10⁷ Pa，单元4的应力为4.167 x 10⁷ Pa 。

调用的函数

function k = Bar2D2Node_Stiffness(E, A, x1, y1, x2, y2, alpha)
% 该函数计算单元的刚度矩阵
% Input：
% E：弹性模量
% A：横截面积
% (x1, y1)：第一个节点坐标
% (x2, y2)：第二个节点坐标
% alpha：角度（单位是度）
% 
% Output：
% k：单元刚度矩阵（4*4）
% 
L = sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
x = alpha*pi/180;
C = cos(x);
S = sin(x);
k = E*A/L * [C*C C*S -C*C -C*S;C*S S*S -C*S -S*S;-C*C -C*S C*C C*S;-C*S -S*S C*S S*S];
end

function z = Bar2D2Node_Assembly(KK, k, i, j)
% 该函数进行单元刚度矩阵的组装
% Input：
% k：单元刚度矩阵
% i，j：节点编号
% 
% Output：
% KK：整体刚度矩阵
% 
DOF(1) = 2*i-1;
DOF(2) = 2*i;
DOF(3) = 2*j-1;
DOF(4) = 2*j;
for n1 = 1:4
    for n2 = 1:4
        KK(DOF(n1), DOF(n2)) = KK(DOF(n1), DOF(n2)) + k(n1, n2);
    end
end
z = KK;
end

function force = Bar2D2Node_Force(E, A, x1, y1, x2, y2, alpha, u)
% 该函数计算单元的节点力向量
% Input：
% k：单元刚度矩阵
% u：单元位移列阵（2*1）
% 
% Output：
% force：单元节点力向量（2*1）
% 
L = sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
x = alpha*pi/180;
C = cos(x);
S = sin(x);
force = E*A/L*[-C -S C S]*u;
end

function stress = Bar2D2Node_Stress(E, x1, y1, x2, y2, alpha, u)
% 该函数计算单元的应力
% Input：
% E：弹性模量
% (x1, y1)：第一个节点坐标
% (x2, y2)：第二个节点坐标
% alpha：角度（单位是度）
% u：单位节点位移向量
% 
% Output：
% stress：单元应力
% 
L = sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
x = alpha*pi/180;
C = cos(x);
S = sin(x);
stress = E/L*[-C -S C S]*u;
end

利用ANSYS进行求解

FINISH
/CLEAR
/PREP7                                                       ! 进入前处理
/PLOPTS, DATE, 0                                             ! 设置不显示日期和时间

! 设置单元、材料、生成节点及单元
ET, 1, LINK1                                                 ! 选择单元类型
UIMP, 1, EX, , , 2.95e11,                                    ! 给出材料的弹性模量
R, 1, 1e-4,                                                  ! 给出实常数（横截面积）
N, 1, 0, 0, 0,                                               ! 生成1号节点（0，0，0）
N, 2, 0.4, 0, 0,                                             ! 生成2号节点（0.4，0，0）
N, 3, 0.4, 0.3, 0,                                           ! 生成3号节点（0.4，0。3，0）
N, 4, 0, 0.3, 0,                                             ! 生成4号节点（0，0.3，0）
E, 1, 2                                                      ! 生成1号单元
E, 2, 3                                                      ! 生成2号单元
E, 1, 3                                                      ! 生成3号单元
E, 4, 3                                                      ! 生成4号单元
FINISH                                                       ! 结束前处理

! 在求解模块中，施加位移约束、外力，进行求解
/SOLU                                                        ! 进入求解状态
D, 1, ALL                                                    ! 将1号节点的位移全部固定
D, 2, UY                                                     ! 将2号节点的Y方向位移固定
D, 4, ALL                                                    ! 将4号节点的位移全部固定
F, 2, FX, 20000,                                             ! 在2号节点处施加X方向的力20000
F, 3, FY, -25000,                                            ! 在3号节点处施加Y方向的力-25000
SOLVE                                                        ! 进行求解
FINISH                                                       ! 结束求解状态

! 进入一般的后处理模块
/POST1                                                       ! 进入后处理
PLDISP, 1                                                    ! 显示变形状况
FINISH                                                       ! 结束后处理

位移云图：

各个结点的位移：

各个节点的反力：

与前面MATLAB求解计算的结果相同。

注：

参考曾攀老师著《有限元基础教程》以及P.I.Kattan著含来彬译《MATLAB有限元分析与应用》。