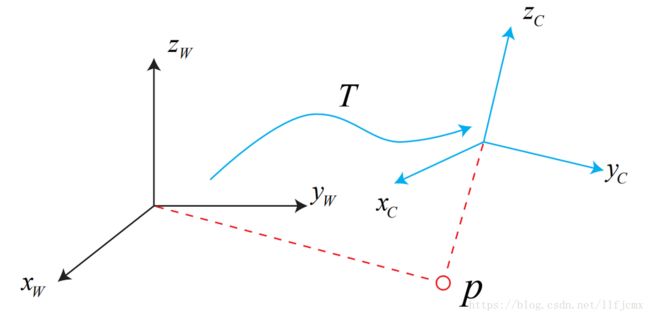
三维空间刚体运动的描述总结

三维空间刚体运动的描述方式有很多种，大概是：

旋转矩阵、平移向量--->欧式变换矩阵--->旋转向量--->欧拉角--->四元数

下面对它们简单的做一个整理，顺一下思路。

欧式变换中，坐标系的变换有：旋转、平移两种情况（只有旋转、只有平移、两者都有）

1、旋转矩阵、平移向量

假设此时，相机坐标系相对于世界坐标系的旋转矩阵为R、平移向量为t，则

这里要注意的就是“R、t是从哪个坐标系到哪个坐标系的，一定不能弄错了”，R是一个行列式为1的正交矩阵。

2、欧式变换矩阵

用R、t来表示欧式空间的旋转和平移存在一个问题：变换关系不是一个线性关系，多次变换之后计算公式会变得过于复杂。

于是就引入了齐次坐标：在三维向量的末尾添加一维（为数字1），将其变成四维向量，这种形式的坐标就是齐次坐标。

在齐次坐标里边，某个点的具体坐标不是唯一确定的，比如说[1, 1, 1, 1]和[2, 2, 2, 2]表示的是同一个点。但是，如果最后一项不为0，我们可以将其转换为“归一化坐标”---所有坐标除以最后一项，也就是将齐次坐标转换为非齐次坐标，对于每一个点来说，它的归一化坐标一定是唯一的。用公式表示就是：。

引入了其次坐标之后，我们可以将R、t写在一个矩阵里面，如下：

中间的矩阵称为欧式变换矩阵，使用这种形式的欧式变换矩阵的好处就是它是一种线性变换的形式，多次变换直接将欧式变换矩阵左乘就可以得到最终的变换矩阵。

3、旋转向量

欧式变换可以很好的描述的刚体的运动，并且还是线性的形式。为了还需要旋转向量？

1. 欧式变换矩阵用9个变量描述6个自由度的运动，信息有冗余
2. 欧式变换矩阵本身是行列式为1的正交矩阵，这样的约束会使得后面优化的求解变得苦难。

旋转向量表示旋转的思想就是：任意一个旋转都可以用旋转轴和旋转角来表示。

因此，我们可以让旋转向量的方向和旋转轴相同，旋转向量的模表示旋转角。

旋转向量用3个自由度描述旋转，再用平移向量来描述平移向量，这样刚好可以用6个自由度来表达一次变换。

旋转向量和旋转矩阵之间的转换---罗德里格斯公式：

1. 若旋转轴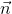为，旋转角为，则旋转矩阵为：
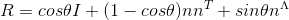
2. 若已经旋转矩阵，求旋转角：

                                   

                                             

          于是：

          同时，旋转轴经过旋转之后不变，则有，解方程即可得到旋转轴。

4、欧拉角

相比旋转欧式、欧式变换矩阵、旋转向量，欧拉角以一种更加直观的方式来表示旋转---三个轴上分离的转角。

欧拉角的一个缺点就是存在“万向锁问题”。

5、四元数

四元数的形式如下：或者，其中

单位四元数可以用来表示三维空间中任意一个旋转，这种表达方式和欧式变换矩阵、欧拉角是等价的。

（1）四元数和旋转向量之间的转换

假设某个旋转是绕单位向量进行了角度为，那么这个旋转对应的四元数为：

 相反，若已知一个单位四元数为，可以从它计算出旋转轴和夹角：

，

上面式子中的加上，得到一个完全相同的旋转，但是对应的四元数却成为一个负的。在四元数中，任意一个旋转，都可以用两个互为相反数的四元数来表示。

（2）用四元数表示旋转

假设一个空间三维点，以及一个由轴角指定的旋转，经过旋转之后变为点。

它们之间的关系可以用下列式子来表达：

1. 把三维空间点用一个纯四元数来描述：
2. 把旋转用四元数表示：
3. 旋转之后的点为：

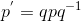
可以验证，计算结果的实部为0，也就是一个纯四元数。虚部的3个分量表示旋转后的点的坐标。

（3）四元数到旋转矩阵的转换---见SLAM十四讲P55。

下面是一道练习题：

机器人1号、2号分别位于世界坐标系中。

1号的位姿：q1=[0.25,0.2,0.3,0.1]，t1=[0.3,0.1,0.1]

2号的位姿：q2=[-0.5,0..4,-0.1,0.2]，t2=[-0.1,0.5,0.3]

注意：这里的q、t表达的是Tcw，且未进行归一化。

设点p在机器人1号的坐标系下的坐标为p=[0.5,0,0.2]，求它在机器人2号的坐标系下的坐标。

#include 
#include 
#include 
//Geometry模块提供了各种旋转和平移的表示
#include 

using namespace std;

int main()
{
	//一号的姿态
	Eigen::Quaterniond q1(0.35, 0.2, 0.3, 0.1);
	Eigen::Vector3d t1(0.3, 0.1, 0.1);

	Eigen::Isometry3d Tcw_1 = Eigen::Isometry3d::Identity();
	Tcw_1.rotate(q1.normalized().matrix());	//q1.matrix()将四元数转为AngleAxis旋转向量
	Tcw_1.pretranslate(t1);

	//点P
	Eigen::Vector3d Pc1(0.5, 0, 0.2);
	Eigen::Vector3d Pw = Tcw_1.inverse()*Pc1;

	//二号的姿态
	Eigen::Quaterniond q2(-0.5, 0.4, -0.1, 0.2);
	Eigen::Vector3d t2(-0.1, 0.5, 0.3);

	Eigen::Isometry3d Tcw_2 = Eigen::Isometry3d::Identity();
	Tcw_2.rotate(q2.normalized().matrix());
	Tcw_2.pretranslate(t2);

	Eigen::Vector3d Pc2 = Tcw_2*Pw;

	cout << "p向量在小萝卜二号的坐标系下的坐标为：" << endl;
	cout << "(" << Pc2.x() << "," << Pc2.y() << "," << Pc2.z() << ")" << endl;

	return 0;
}