数学建模方法自己归纳总结（建模参考用，包含相应例题以及MATLAB代码）
各类方法概述：
预测判别方法：
- BP神经网络
- 模糊识别
- 贝叶斯判别
分类方法：
- 模糊聚类分析（模糊数学，模糊矩阵，k截矩阵）
- K-means聚类分析
- 系统聚类分析
综合评价：
- 灰色关联（贴近度）
- 因子分析综合评价（主成分分析反过来，找隐藏的综合评价因子）
- TOPSIS评价（正贴近度，负贴近度）
- 模糊综合评价（与单因素评价结合，有多级模糊综合评价）
分析方法：
- 定权法：层次分析定权法，熵权定权法，均方差定权法
- 主成分分析思想
- 通经分析：
#仅仅研究两个变量之间的关系：简单相关系数
多个相关变量中研究两个变量之间的关系：偏相关系数
多个不相关变量与一个因变量之间的关系：多元回归
多个相关的自变量与一个因变量之间的关系：通经分析
多个相关的因变量和多个相关的自变量之间的关系：典型相关性分析 - 非参数统计分析
a. 两组样本的非参数检验
1） 配对样本数据符号检验法
2） 两组配对样本非参数秩和检验法（更精细）
3） 两组样本非参数检验（非配对）（秩和检验）
b. 多组独立样本的非参数检验
1） 多组独立样本的H检验法（单向秩次方差分析法）（最强方法）（总体不服从正态分布或无法确定总体分布 - 单因素方差分析
- 分类变量的独立性检验
- 连个变量之间的相关系数
预测方法
- 多序列回归预测模型（解线性方程组）（多个因变量，多个自变量）
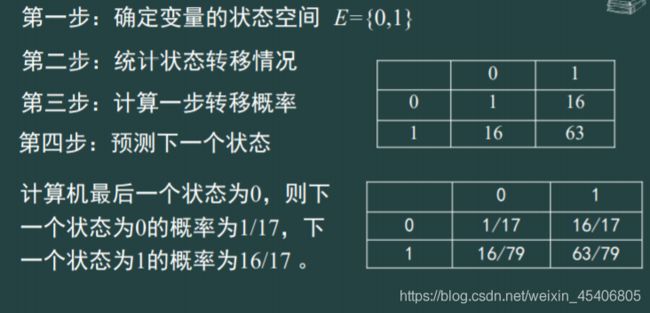
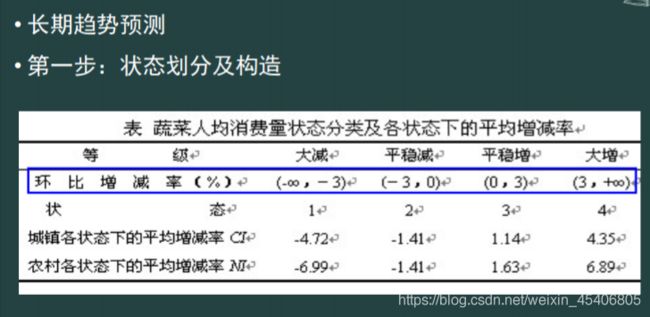
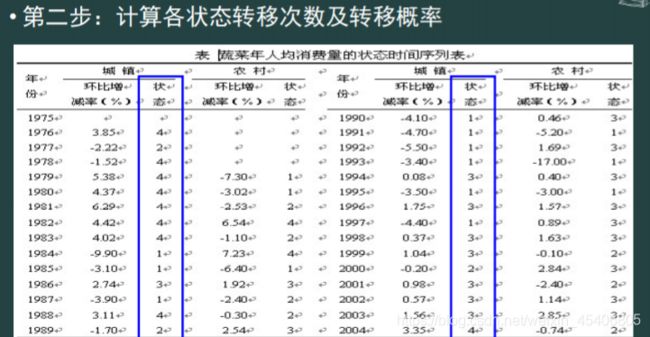
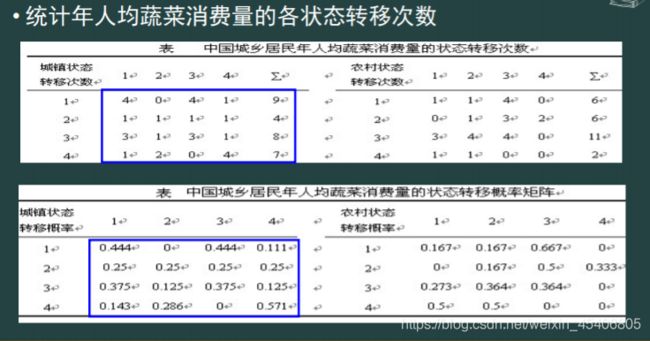
- 随机序列的Markov链预测（马尔科夫链转移矩阵）
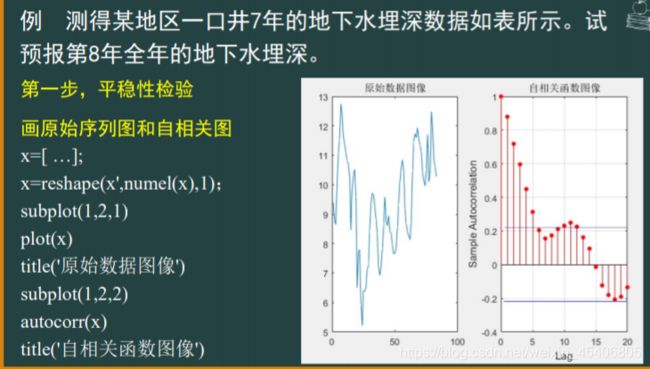
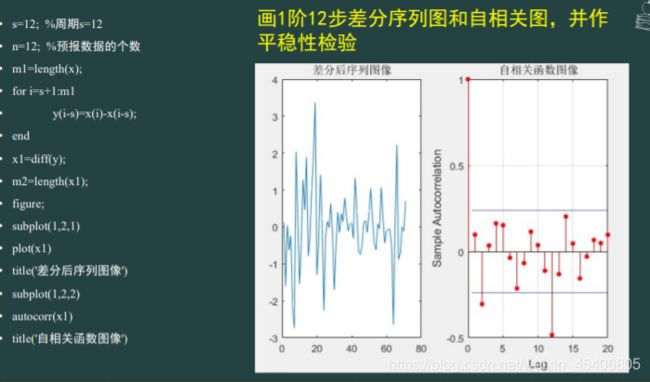
- 时间序列ARIMA预测分析（用多步差分消除周期，单步差分消除趋势，）
（单个自变量，多个因变量）
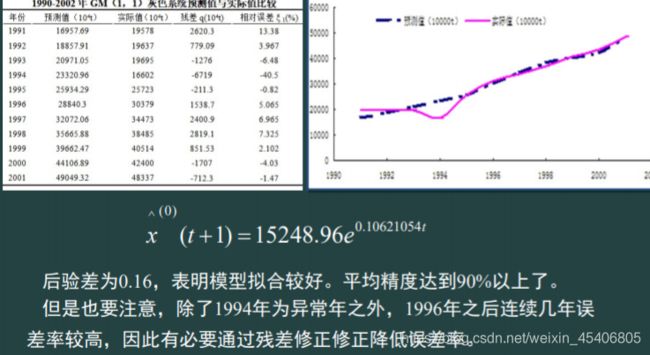
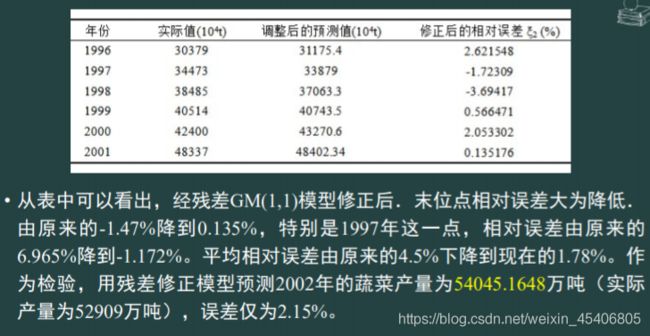
#时间序列分析建模步骤 - 残差修正和新陈代谢灰色预测（数据量小，不服从正态或分布不详，数据具有指数趋势）
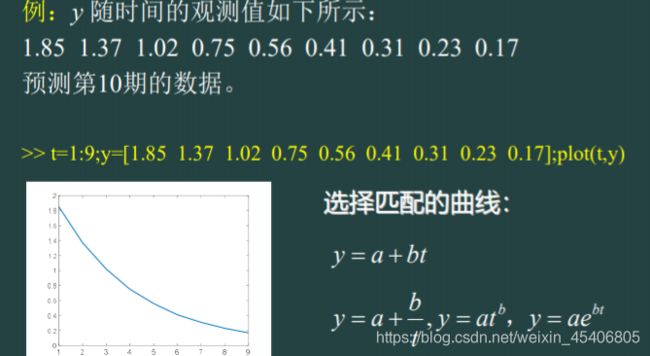
- 单序列时间的回归预测（单个自变量，单个因变量）
其他基本建模操作
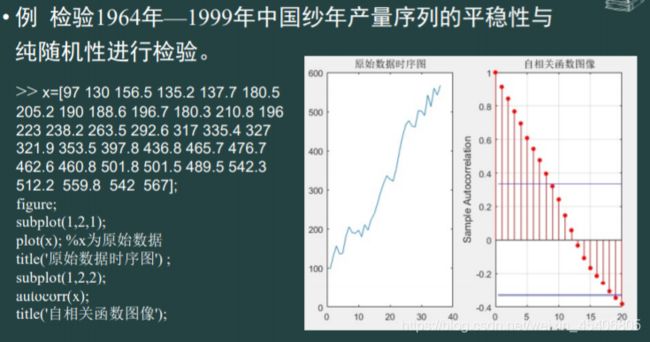
- 单序列数据的正态性检验
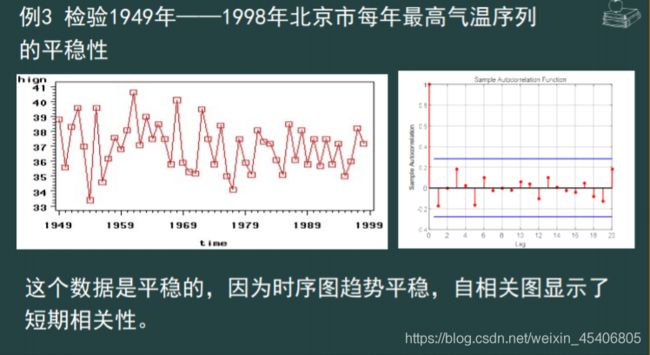
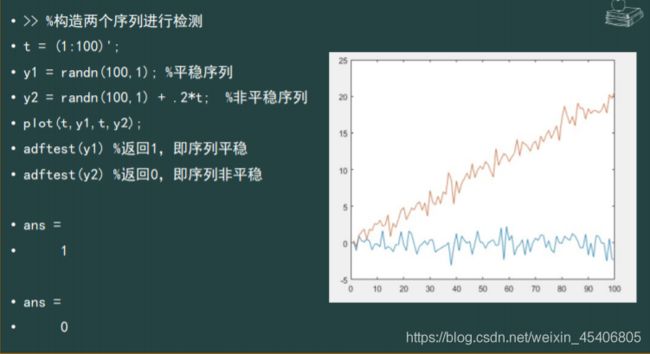
- 单序列数据的平稳性检验
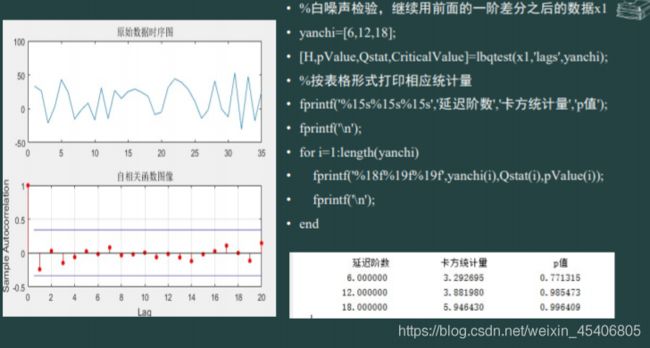
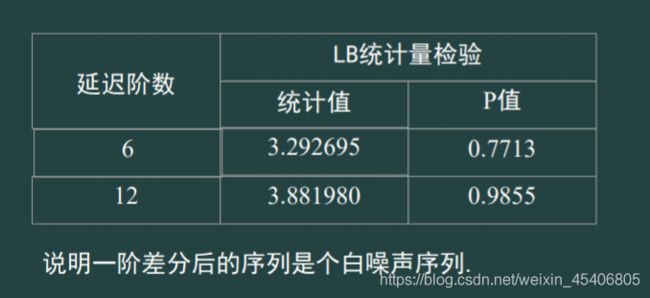
- 单序列数据的白噪声检验
基础知识：
- MATLAB基本操作
1） 基本操作与运算
2） 函数文件
3） 条件语句
4） 循环语句 - 统计学基础知识：
1） 常见统计量及分布
2） 假设检验思想与应用
3） 特征值与特征向量
4） 回归模型的思想及应用
各类方法详细描述（含代码）
预测判别方法：
- BP神经网络
//分析建模
/*
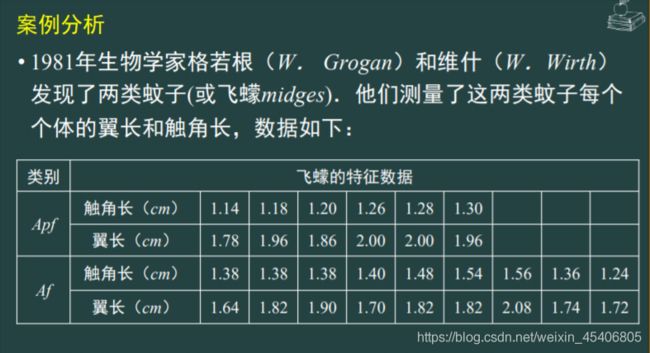
->将问题看作一个系统，飞蠓的数据作为输入，非盟的类型作为输出，研究输入与输出的关系。输入的数据有15个，即，
p=1,...,15;j=1,2对应15个输出
->建立一个只有输入层与输出层的神经网络模型，输入层采用tansig激发函数，输出层采用purelin激发函数。
->为了便于计算机处理，可以将符号数字化。将Apf类记为0.利用MATLAB中的ANN工具箱函数，编写如下程序：*/
p=[1.14 1.18 1.20 1.26 1.28 1.30 1.38 1.38 1.38 1.40 1.48 1.54 1.56 1.36 1.24;
1.78 1.96 1.86 2.00 2.00 1.96 1.64 1.82 1.90 1.70 1.82 1.82 2.08 1.74 1.72];
%输入两种飞蠓的参数
t=[1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 ];%两种飞蠓的类别
net=newff(minmax(p),[2,1],{
'tansig','purelin'}); %建立一个具有两层的神经网络
net.trainParam.show=50;%显示训练结果的间隔步数
net.trainParam.epochs=1000;%训练次数
net.trainParam.goal=1e-2;%设置训练参数
net=train(net,p,t);
pp=[1.24 1.28 1.40 ;1.80 1.84 2.04};%输入需要判别的三只飞蠓参数
y=sim(net,pp) %利用已经训练好的网络识别三只飞蠓
y=
0.4172 0.3846 0.7132
- 模糊识别(贴近度）
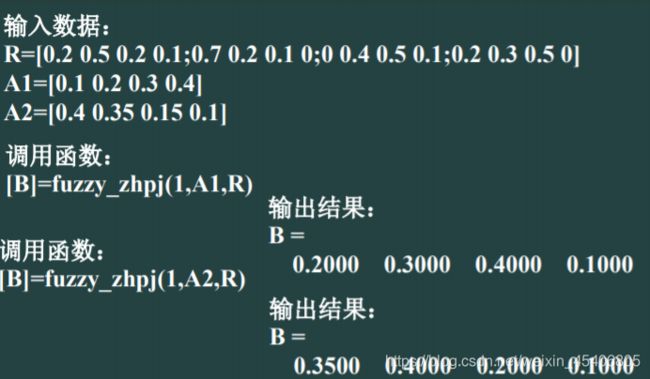
//输入数据
A=[1 0.8 0.5 0.4 0 0.1;
0.5 0.1 0.8 1 0.6 0;
0 1 0.2 0.7 0.5 0.8;
0.4 0 1 0.9 0.6 0.5;
0.8 0.2 0 0.5 1 0.7;
0.5 0.7 0.8 0 0.5 1];
B=[0.7 0.2 0.1 0.4 1 0.8];
//调用函数
[C]=fuzzy_mssb(2,A,B)
//输出结果
C=
0.3333 0.3778 0.4545 0.4348 0.8824 0.4565
- 贝叶斯判别
//代码解释
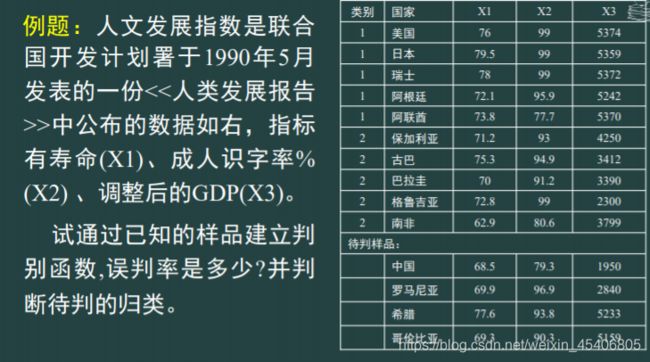
[jg,wpl,gl]=classify(pb,xl,lb);
pb指带判别的数据集，行是样本，列代表指标；
xl指训练样本，行是样本，列代表指标；
lb指训练样本的类别，列向量；
jg指的是判别结果，即pb数据集中每一个行的样本点属于的类别；
wpl指的是总的误判率；
gl指的是panbic数据集中每一个样本点属于每一类的概率
//计算代码如下
>>[x,textdata]=xlsread('bayes.xls‘）；
>pb=x(1:14,3:5);
>xl=x(1:10;3:5);
>lb=x(1:10,1);
>gj=testdata(2:15,2);
>[jg,wpl,gl]=classify(pb,xl,lb);
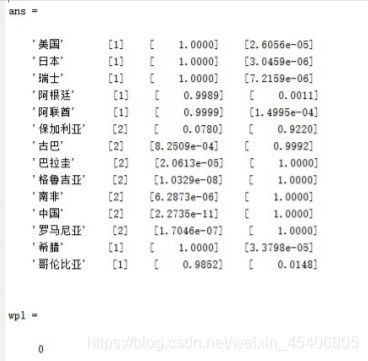
>[gj,num2cell([jg,gl])]
>wpl
>
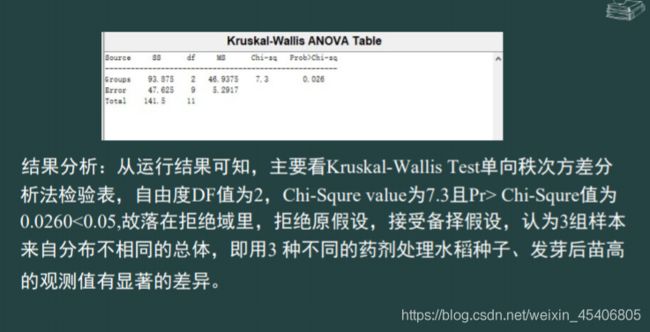
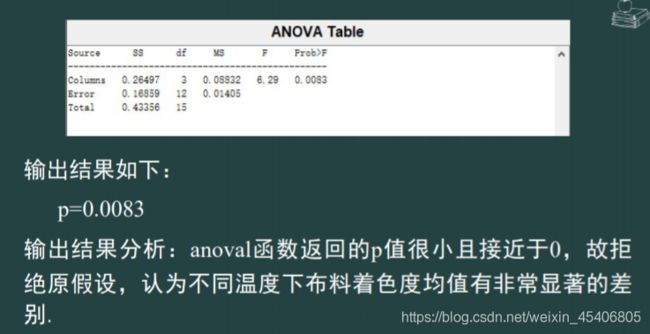
从运行结果可以看出
中国和罗马尼亚属于第二类，希腊和哥伦比亚属于第一类
误判率是0，说明训练的样本训练的效果相当的好，没有出现反常的点
#注：另外：classify工具箱也可以根据training 和group计算各组出现的频率，作为各组先验概率的估计，详见课件
分类方法：
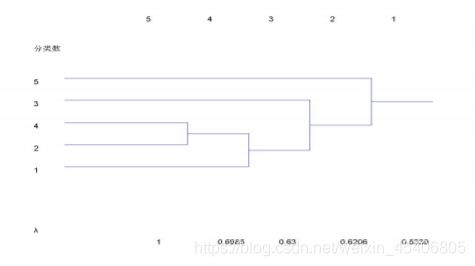
5. 模糊聚类分析（模糊数学，模糊矩阵，k截矩阵）
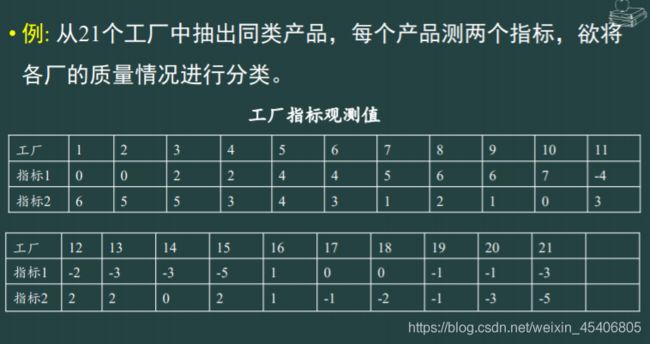
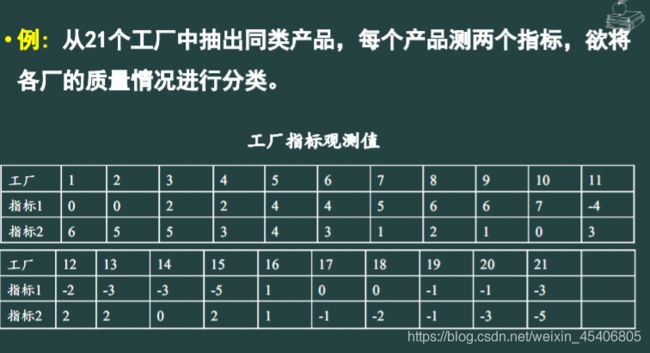
例子：考虑某环保部门对于该地区5个环境区域X={
x1,x2,x3,x4,x5}
按照按污染情况进行分类。设每个区域包括空气、水分、土壤、作物4个
要素，环境区域的污染情况由污染物在4个要素的含量超过情况来衡量。
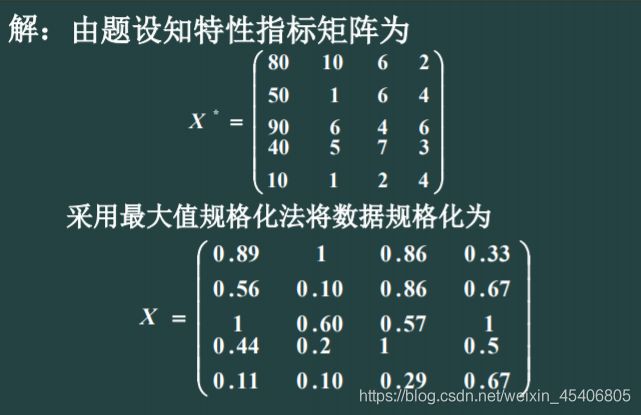
设这5个环境区域的污染数据为
x1=(80,10,6,2),x2=(50,1,6,4),x3=(90,6,4,6),
x4=(40,5,7,3),x5=(10,1,2,4).
试对X进行分类
//代码
X=[80 10 6 2;50 1 6 4 ;90 6 4 6;40 5 7 3;10 1 2 4]
//调用函数
fuzzy_jlfx(3,5,X)
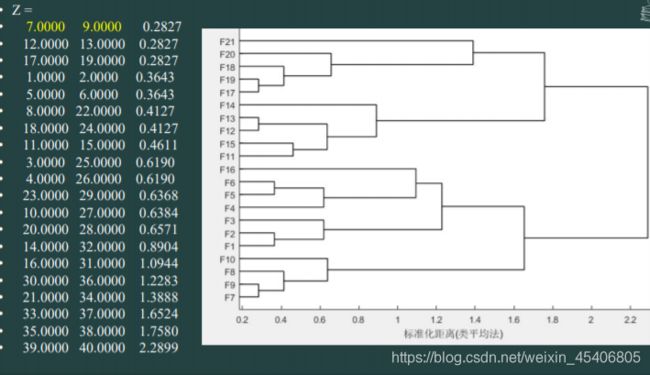
输出动态聚类图如下
- K-means聚类分析
//程序
[data,testdata]=xlsread('xtjl.xls');
gc=textdata(2:end,1);
data=zscore(data);
x1=data(:,1);x2=data(:,2);scatter(x1,x2,'r');
startdata=data([2,8,12,18],:);
idx=kmeans(data,4,'Start',startdata);
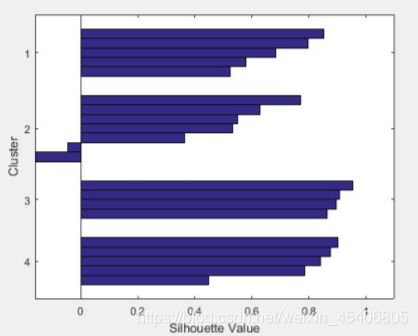
[S,H]=silhouette(data,idx);
gc(idx==1),gc(idx==2),gc(idx==3),gc(idx==4);
[data,textdata]=xlsread('xtjl.xls');
gc=testdata(2:end,1);
data=zscore(data);
idx=kmeans(data,4,'replicates',10);
[S,H]=sihouette(data,idx);
Leibie1=gc(idx==1),Leibie2=gc(idx==2),
Leibie3=gc(idx==3),Leibie4=gc(idx==4)
//分四类还是可以的
- 系统聚类分析
综合评价：
10. 灰色关联（关联度）（分布不必正态，小样本数据，只有排序有意义，本身的关联度没有实际意义）
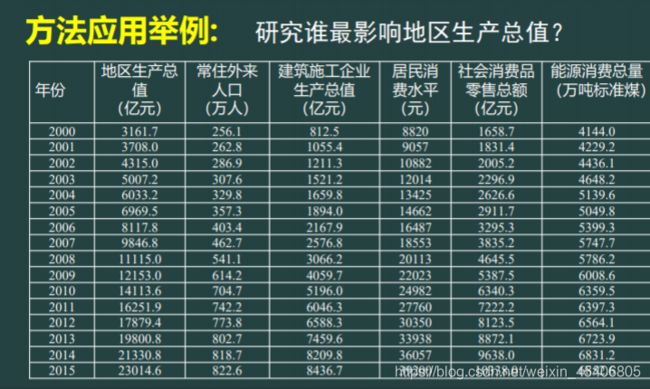
//方法应用举例
//计算步骤如下：
//确定参考数列
clear;
data=xlsread('hsgl.xls','B3:H18');%将数据导入MATLAB默认路径下
[m,n]=size(data);
rou=0.5;
//数据标准化处理
%无量纲化-采用均值法
avedata=mean(data);%每列的均值
for i=1:m
newdata(i,:)=data(i,:)./avedata;%无量纲化后的序列数据
end
//关联系数的计算
for j=2:n
diff(:,j-1)=abs(newdata(:,1)-newdata(:,j));%差的绝对值
end
%最大最小极差--采用总极差法
maxdiff=max(max(diff));%最大极差
mindiff=min(min(diff));%最小极差
for i=1:m
for j=1:n
correlation(i,j)=(mindiff+rou*maxdiff)/(diff(i,j)+rou*maxdiff);
end
end
correlationnew=mean(correlation)
corelationnew=
0.7665 0.7749 0.8109 0.9273 0.5800
- 因子分析综合评价（主成分分析反过来，找隐藏的综合评价因子）
//分析：
//由于指标个数较多，不便于分析排序。
//因此，考虑先做因子分析找出指标的共同因子，
//再计算因子得分，通过分析因子得分来评价该地区的经济指标
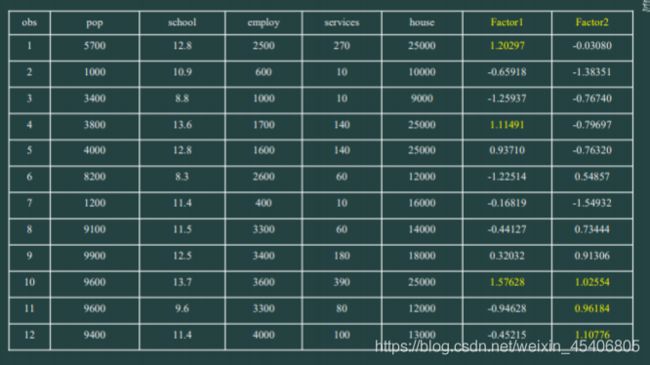
x=xlsread('factor.xls');%调出数据
bzhx=zscore(x);%按照列向量做标准化
r=corrcoef(bzhx);%做相关系数矩阵
[vecl,tzl,conl]=pcacov(r);%直接给出特征向量，
%由特征根降序排列，vecl特征向量，
%tzl特征值，conl累计贡献率
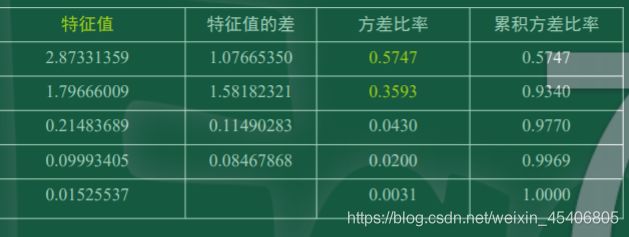
//结果表明，5个因子对应的特征值，特征值表示因子贡献率。
//通常确定因子个数时，要求因子的累计贡献率大于80%
//结果表明应该选取2个因子，记为F1，F2
//贡献率分别为57.47% 35.93%
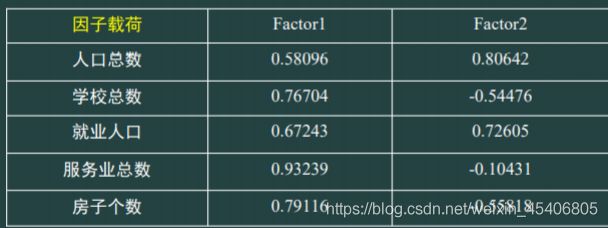
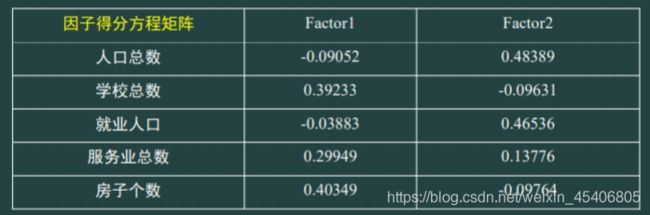
A=vecl*sqrt(diag(tzl));%因子载荷矩阵
//对于实际问题，公共因子的实际意义不好解释。
//因此考虑将指标的系数极值化，
//即让系数趋近于0或1，趋近于1说明公共因子与该指标密切相关，
//否则趋近于0时说明相关程度很低。
//因此，要做因子方差极大旋转
%进行方差极大旋转，直接低矮用factoran计算结果与下面不同
am=A(:,1:2);
[bm,t]=rolatefactors(am,'method','varimax');
//这个表示因子旋转阵，为旋转后得到的因子载荷矩阵。
//再保证正交轴的性质不变，每一行的平方和不变的前提下，
//每一列数据的方差已经达到极大
coef=inv(r)*bm;score=bzhx*coef;
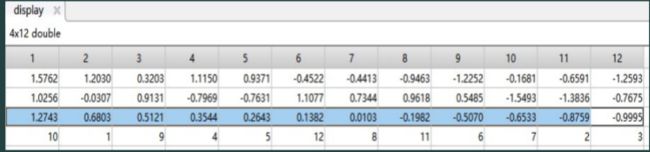
Tscore=score*conl(:,1:2);%综合评价
[STscore,ind]=sort(Tscore,'descend');%对地区进行排序
display=[score(ind,:)';STscore';ind'];%显示排序结果
- TOPSIS评价（正贴近度，负贴近度）
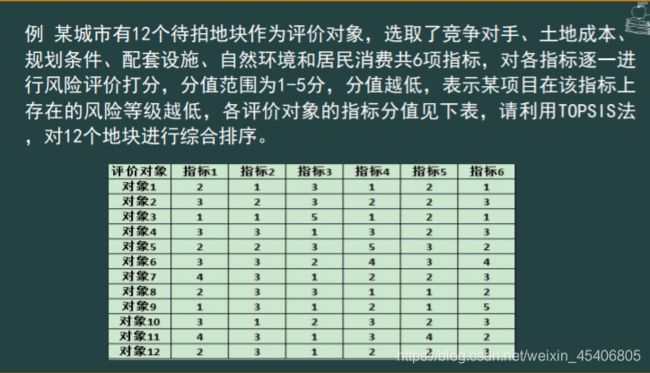
%将原始数据按照规定格式输入到data_topsis.xls中
%L存放各个指标的指示值
>>L=xlsread('data_topsis.xls','B4:G4');
>X=xlsread('data_topsis.xls','B6:G17');
>W=xlsread('data_topsis.xls','B19:G19');
>[m,n]=size(X);
>V=zeros(m,n);
>for i=1:m
> for j=1:n
> %根据指标指示值判断是越大越优型指标还是越小越优型指标
> if L(j)==1 %越大越优型指标的标准化(其实就是消去量纲）
> V(i,j)=(X(i,j)-min(X(:,j)))/(max(X(:,j))-min(X(:,j)））；
> else
> %越小越优型指标的标准化（其实是消去量纲）
> V(i,j)=(max(X(:,j))-X(i,j))/(max(X(:,j))-min(X(:,j)));
> end
> end
>end
>%构建加权决策矩阵
>R=zeros(m,n);
>for i=1:m
> for j=1:n
> R(i,j)=W(j)*V(i,j);
> end
> end
> %计算正理想解和负理想解
> SP=zeros(1,n);
> SM=zeros(1,n);
> for j=1:n
> %根据指标指示值判断是越大越优型指标还是越小越优型指标
> if L(j)==1
> %越大越优型指标的正理想解和负理想解
> SP(j)=max(R(:,j));%正理想解
> SM(j)=min(R(:,j));%负理想解
> else
> %越小越优型指标的正理想解和负理想解
> SP(j)=min(R(:,j));%正理想解
> SM(j)=max(R(:,j));%负理想解
> end
> end
>%计算各个方案与正理想解的距离
>SdP=zeros(1,m);
>for i=1:m
> s=0;
> for j=1:n
> s=s+(SP(j)-R(i,j))^2;
> end
> SdP(i)=sqrt(s);
>end
>%计算各个方案与负理想解的距离
>SdM=zeros(1,m);
>for i=1:m
> s=0;
> for j=1:n
> s=s+(SM(j)-R(i,j))^2;
> end
> SdM(i)=sqrt(s);
>end
>%计算贴近度
>yita=zeros(1,m);
>for i=1:m
> yita(i)=SdM(i)/(SdP(i)+SdM(i));
>end
>disp('贴近度为：');
>yita
>//求解过程中，我们首先利用熵值法求出六个指标的熵权，
>即权重，依次为
>W=0.1531 0.5269 0.0746 0.0837 0.0766 0.0851
>再利用TOPSIS方法，对12个地块进行综合排序
>最后求得12个地块的贴近度为
>yit=
> 0.1097 0.5035 0.1227 0.8187
> 0.4964 0.8650 0.8237 0.7580
> 0.7305 0.1853 0.8390 0.7733
>注：此处贴近度越小，说明项目的风险越小。
>根据计算结果，排序后，1号地可以作为首选投资项目
- 模糊综合评价（与单因素评价结合，有多级模糊综合评价）
一级综合评价
二级综合评价
分析方法：
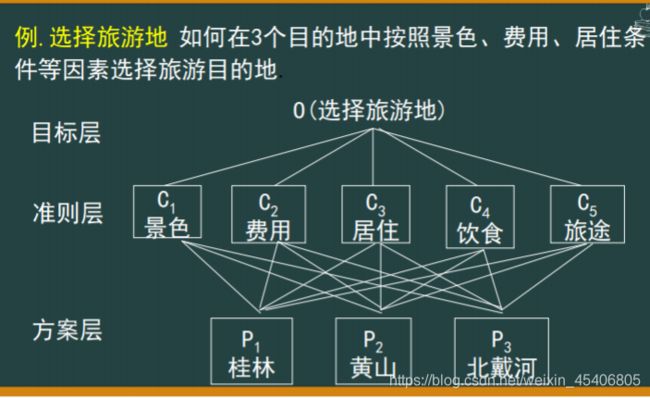
19. 定权法：层次分析定权法，熵权定权法，均方差定权法
层次分析法
模型求解程序
clear;
clc;
n1=5;%准则层的判断矩阵阶数
A=[1 1/2 4 3 3;2 1 7 5 5;1/4 1/7 1 1/2 1/3;1/3 1/5 2 1 1;1/3 1/5 3 1 1];
%准则层的判断矩阵
RI=[0 0 0.58 0.90 1.12 1 24 1.32 1.41 1.45];%平均随机一致性指标RI
[x,y]=eig(A);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/(sum(x(:,num))
cr0=(lamda-n1)/(n1-1)/RI(n1)
w0=
0.2636
0.4758
0.0538
0.0981
0.1087
cr0=
0.0161
熵权定权法
[m,n]=size(X);
%矩阵X消除量纲后得到R
R=zeros(m,n);%零矩阵
for i=1:m
for j=1:n
%根据指标指示值判断是越大越优型指标还是越小越优型指标
if L(j)==1
%越大越优型指标的标准化
R(i,j)=(X(i,j)-min(X(:,j)))/(max(X(:,j))-min(X(:,j))）；
else
%越学越优型指标的标准化
R(i,j)=(max(X(:,j)))-X(i,j))/(max(X(:,j))-min(X(:,j))）；
end
end
end
%给第j项指标对不同评价对象求和，得SumR
sumR=sum(R);
%初始化特征比重矩阵p
p=zeros(m,n);%零矩阵，可有可无
%计算第i个评价对象第j项指标的特征比重p
for i=1:m
for j=1:n
p(i,j)=R(i,j)/sumR(j);
end
end
%判断p中元素是否为0，如果为0，p(i,j)*ln(p(i,j))=0
%用中间变量tp表示：p(i,j)*ln(p(i,j))
tp=zeros(m,n);%零矩阵，可有可无
for i=1:m
for j=1:n
%根据p(i,j)是否小于等于0给tp赋值
if p(i,j)<=0
tp(i,j)=0
else
tp(i,j)=p(i,j)*log(p(i,j));
end
end
end
%计算第j项指标的条件熵
H=-sum(tp);
%计算第j项指标的熵值
E=H/log(m);
%计算差异系数G
G=1-E;
%计算熵权W
W=G/sum(G)
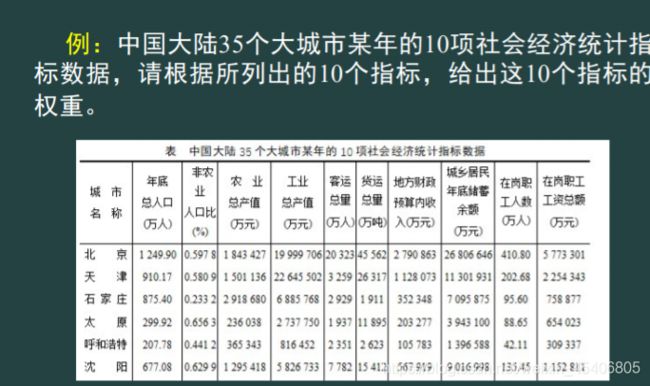
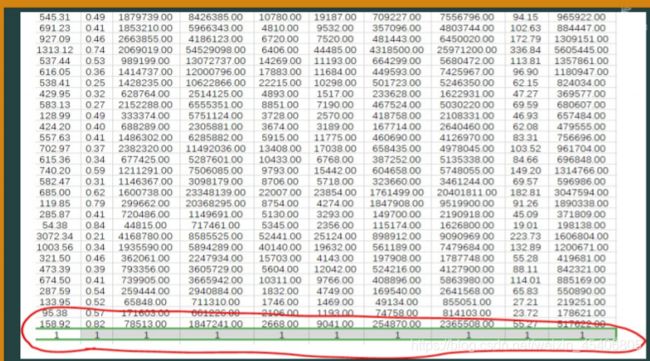
。运行得到权重
W=
0.0768 0.0438 0.0756 0.1338 0.1292 0.1041 0.1336 0.1041 0.0780 0.1211
均方差定权法
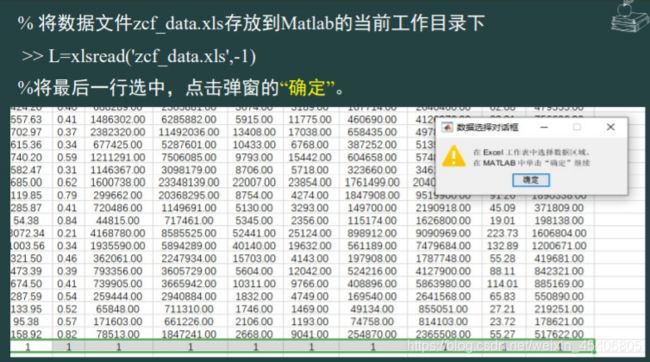
x=xlsreead('zef_data.xls');
[m,n]=size(x);
for j=1:n
sigma2(j)=0;
for i=1:m
v(i,j)=(x(i,j)-min(x(:,j)))/(max(x(:,j))-min(x(:,j)));
sigma2(j)=sigma2(j)+((v(i,j)-mean(v(:,j)).^2));
end
end
sigma=sigma2^.(1/2);
alpha=sigma./sum(sigma)
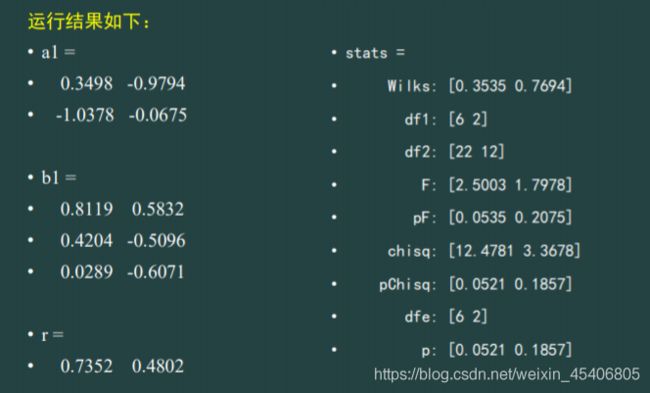
运行结果
alpha=
0.0939 0.1222 0.1111 0.0863 0.0929 0.1048 0.0868 0.1017 0.1033 0.0947
均方差定权的计算步骤
（1)求均值
（2）求均方差
（3）求权重
按照均方差法的步骤
进行四步就求出10个指标的权重，
接着就可以运用加权平均对
消除量纲后的数据进行综合评价。
只需要加一个程序就可以完成
Zh=v*alpha'
- 主成分分析思想
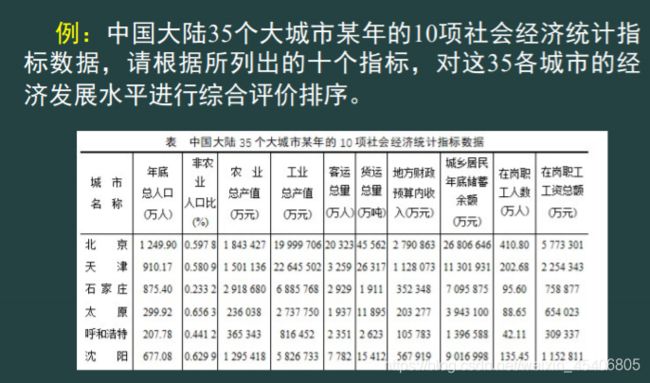
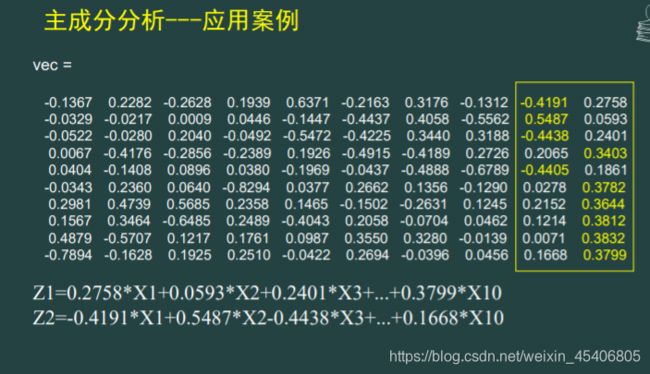
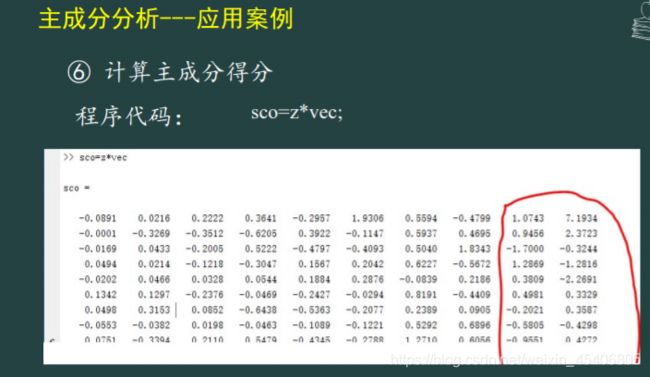
补充：主成分分析与因子分析的关系
鉴于主成分分析现实含义的解释缺陷，统计学斯皮尔曼又对主成分分析进行扩展。因子分析在提取公因子时，不仅注意变量之间是否相关，而且考虑相关关系的强弱，使得提取出来的公因子不仅起到降维的作用，而且能够被很好的解释。因子分析与主成分分析是包含与扩展的关系。
首先解释包含关系。如下图所示，在SPSS软件“因子分析”模块的提取菜单中，提取公因子的方法很多，其中一种就是主成分。由此可见，主成分只是因子分析的一种方法。
其次是扩展关系。因子分析解决主成分分析解释障碍的方法是通过因子轴旋转。因子轴旋转可以使原始变量在公因子（主成分）上的载荷重新分布，从而使原始变量在公因子上的载荷两级分化，这样公因子（主成分）就能够用哪些载荷大的原始变量来解释。以上过程就解决了主成分分析的现实含义解释障碍。
-
典型相关性分析
-
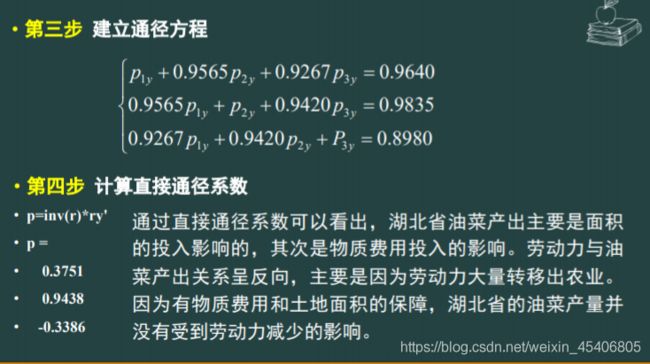
通经分析：
#仅仅研究两个变量之间的关系：简单相关系数
多个相关变量中研究两个变量之间的关系：偏相关系数
多个不相关变量与一个因变量之间的关系：多元回归
多个相关的自变量与一个因变量之间的关系：通经分析
多个相关的因变量和多个相关的自变量之间的关系：典型相关性分析
-
非参数统计分析
c. 两组样本的非参数检验
4） 配对样本数据符号检验法
5） 两组配对样本非参数秩和检验法（更精细）
6） 两组样本非参数检验（非配对）（秩和检验）
d. 多组独立样本的非参数检验
2） 多组独立样本的H检验法（单向秩次方差分析法）（最强方法）（总体不服从正态分布或无法确定总体分布
-
单因素方差分析
-
分类变量的独立性检验
-
连个变量之间的相关系数
简单相关系数
偏相关系数
Spearman等级相关系数
Kendall秩相关系数
预测方法
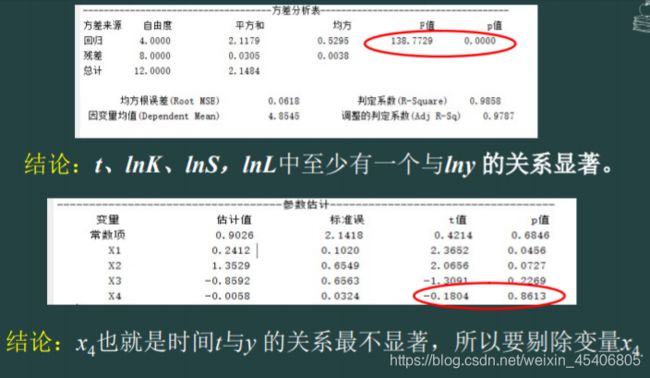
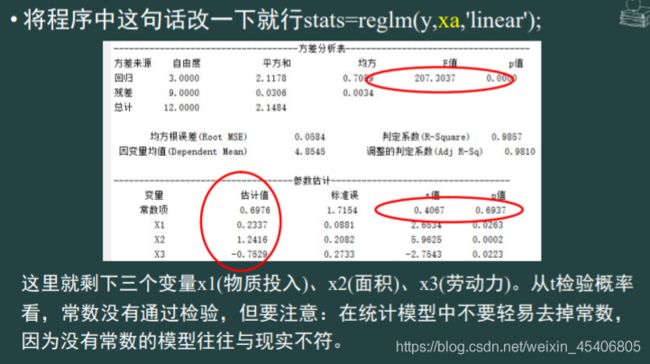
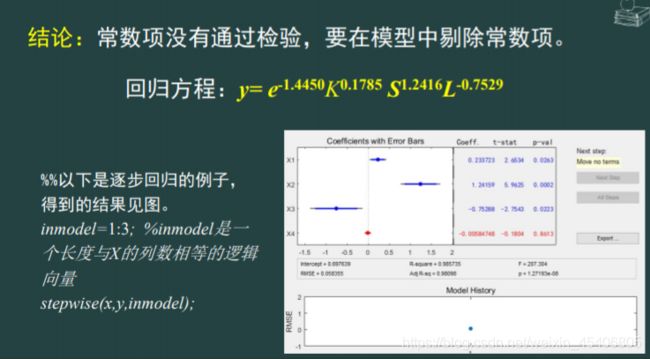
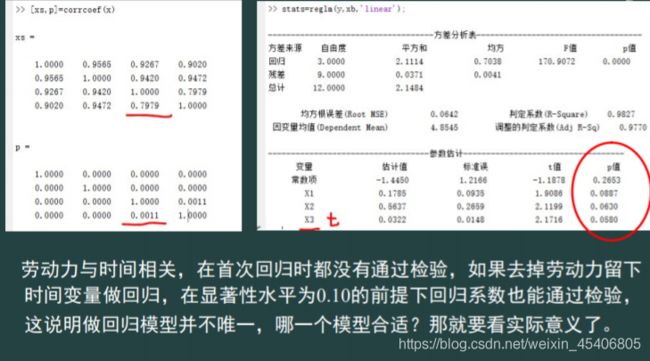
30. 多序列回归预测模型（解线性方程组）（多个因变量，多个自变量）
-
随机序列的Markov链预测（马尔科夫链转移矩阵）
-
时间序列ARIMA预测分析（用多步差分消除周期，单步差分消除趋势，）
（单个自变量，多个因变量）
#时间序列分析建模步骤
-
残差修正和新陈代谢灰色预测（数据量小，不服从正态或分布不详，数据具有指数趋势）
-
单序列时间的回归预测（单个自变量，单个因变量）
其他基本建模操作
36. 单序列数据的白噪声检验
-
单序列数据的平稳性检验
-
单序列数据的正态性检验
基础知识：
40. MATLAB基本操作
5） 基本操作与运算
6） 函数文件
7） 条件语句
8） 循环语句
41. 统计学基础知识：
5） 常见统计量及分布
6） 假设检验思想与应用
7） 特征值与特征向量
8） 回归模型的思想及应用
整理不易，如果对你有帮助的话，请支持一下!
