最短路径 Dijkstra算法的Matlab代码实现
为了搞清楚最短路径的算法过程,自己编写代码实现dijkstra算法寻找路径
% 文件名:dijkstra.m
% 时间:2020年9月12日
% 来源:https://blog.csdn.net/lishan132/article/details/108527271
% 功能:利用dijkstra算法计算两点间的最短路径
% dist:起点与终点之间的最短距离值
% path:最短路径索引
% Distance:最短路径下的距离值
% A:邻接矩阵
% strat:起点编号
% dest:终点编号
function [dist,path,Distance] = dijkstra(A,start,dest)
% 测试数据 A =[0,12,inf,inf,inf,16,14;12,0,10,inf,inf,7,inf;inf,10,0,3,5,6,inf;inf,inf,3,0,4,inf,inf;inf,inf,5,4,0,2,8;16,7,6,inf,2,0,9;14,inf,inf,inf,8,9,0];
% 测试数据 start = 1;
% 测试数据 dest = 4;
% 计算程序运行时间
tic %开始计时
% 初始化操作
p = size(A,1); %计算顶点数目
S(1) = dest; %初始化集合S,已加入到路径中的顶点编号
U = 1:p; %初始化集合U,未加入到路径中的顶点编号
U(dest) = []; %删除终点编号
Distance = zeros(2,p); %初始化所有顶点到终点dest的距离
Distance(1,:) = 1:p;
Distance(2,1:p) = A(dest,1:p);
new_Distance = Distance;
D= Distance; %初始化U中所有顶点到终点dest的距离
D(:,dest) = [];
path = zeros(2,p); %初始化路径
path(1,:) = 1:p;
path(2,Distance(2,:)~=inf) = dest; %距离值不为无穷大时,将两顶点相连
% 寻找最短路径
while ~isempty(U) %判断U中元素是否为空
index = find(D(2,:)==min(D(2,:)),1); %剩余顶点中距离最小值的索引
k = D(1,index); %发现剩余顶点中距离终点最近的顶点编号
%更新顶点
S = [S,k]; %将顶点k添加到S中
U(U==k) = []; %从U中删除顶点k
%计算距离
new_Distance(2,:) = A(k,1:p)+Distance(2,k); %计算先通过结点k,再从k到达终点的所有点距离值
D = min(Distance,new_Distance); %与原来的距离值比较,取最小值
%更新路径
path(2,D(2,:)~=Distance(2,:)) = k; %出现新的最小值,更改连接关系,连接到结点k上
%更新距离
Distance = D; %更新距离表为所有点到终点的最小值
D(:,S) = []; %删除已加入到S中的顶点
end
dist = Distance(2,start); %取出指定起点到终点的距离值
toc %计时结束
% 输出结果
fprintf('找到的最短路径为:');
while start ~= dest %到达终点时结束
fprintf('%d-->',start); %打印当前点编号
next = path(2,start); %与当前点相连的下一顶点
start = next; %更新当前点
end
fprintf('%d\n',dest);
fprintf('最短路径对应的距离为:%d\n',dist);
end
此函数共有3个输入参数,3个输出参数
输入参数说明
A:邻接矩阵,存储各顶点之间的距离值,是一个大小为顶点个数的方阵,对角线元素为0
strat:起点编号
dest:终点编号
输出参数说明
dist:指定起点与终点之间的最短距离值
path:最短路径索引,一共两行,第一行的值依次为各顶点编号,第二行的值为与第一行顶点相连的顶点编号
Distence:最短路径下的距离值,一共两行,第一行的值依次为各顶点编号,第二行的值为对应顶点到终点的最小距离值
算法有效性的测试如下:
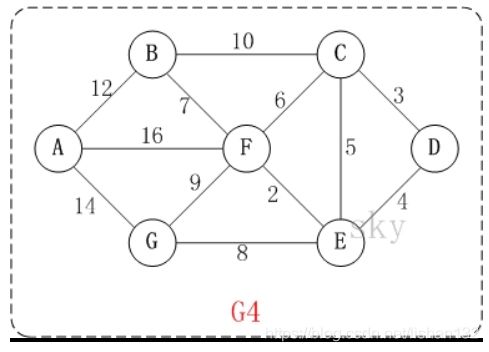
根据上图,想计算A点到D点的最短路径和距离,经过理论分析,其最短路径应为A-->F-->E-->D,最短距离为16+2+4=22
下面输入代码进行验证
输入代码
A =[0,12,inf,inf,inf,16,14;12,0,10,inf,inf,7,inf;inf,10,0,3,5,6,inf;inf,inf,3,0,4,inf,inf;inf,inf,5,4,0,2,8;16,7,6,inf,2,0,9;14,inf,inf,inf,8,9,0];
start = 1;
dest = 4;
[dist,path,Distance] = dijkstra(A,start,dest)时间已过 0.005424 秒。
找到的最短路径为:1-->6-->5-->4
最短路径对应的距离为:22
dist =
22
path =
1 2 3 4 5 6 7
6 3 4 4 4 5 5
Distance =
1 2 3 4 5 6 7
22 13 3 0 4 6 12
输入其他任意两个点,换一个距离矩阵,依然能正确输出最短路径和相应的距离值,算法的有效性得到验证
输入以下代码可生成最终的最短路径图,输出结果与起点值无关,任意点到D点的最短路径均可从图中找到
A =[0,12,inf,inf,inf,16,14;12,0,10,inf,inf,7,inf;inf,10,0,3,5,6,inf;inf,inf,3,0,4,inf,inf;inf,inf,5,4,0,2,8;16,7,6,inf,2,0,9;14,inf,inf,inf,8,9,0];
start = 1;
dest = 4;
[~,path,Distance] = dijkstra(A,start,dest)
path(:,dest) = [];
Distance(:,dest) = [];
s = path(1,:);
t = path(2,:);
weights = Distance(2,:);
names = {'A' 'B' 'C' 'D' 'E' 'F' 'G'};
g = digraph(s,t,weights,names);
plot(g,'EdgeLabel',g.Edges.Weight)可以看到,图中所有点均向D点聚集,且显示了每一个点到D点的最短距离
下面,使用matlab图论工具箱的函数寻找最短路径,再进行一个对比验证
图论工具箱中求最短路径的函数有以下3个,本文使用shortestpath,matlab命令窗口中输入doc shortestpath即可查看用法
shortestpath 两个单一节点之间的最短路径
shortestpathtree 从节点的最短路径树
distances 所有节点对组的最短路径距离
% 文件名:shortpath.m
% 时间:2020年9月12日
% 来源:https://blog.csdn.net/lishan132/article/details/108527271
% 功能:利用matlab自带的shortestpath函数计算两点间的最短路径
% dist:起点与终点之间的最短距离值
% path:最短路径
function [dist,path] = shortpath(A,start,dest)
%使用matlab自带的函数计算最短路径
tic
A(A==inf) = 0; %将无穷大值变为0
[t,s,weights] = find(A); %邻接矩阵中非零值的列、行号索引,及对应值
G = digraph(s,t,weights); %生成一幅带权值的有向图
[path,dist] = shortestpath(G,start,dest); %计算最短路径
toc
%展示结果
plot(G,'EdgeLabel',G.Edges.Weight)
fprintf('找到的最短路径为:');
fprintf('%d ',path);
fprintf('\n');
fprintf('最短路径对应的距离为:%d\n',dist);
end
命令窗口输入以下代码验证结果
A =[0,12,inf,inf,inf,16,14;12,0,10,inf,inf,7,inf;inf,10,0,3,5,6,inf;inf,inf,3,0,4,inf,inf;inf,inf,5,4,0,2,8;16,7,6,inf,2,0,9;14,inf,inf,inf,8,9,0];
start = 1;
dest = 4;
[dist,path] = shortpath(A,start,dest)
时间已过 0.002112 秒。
找到的最短路径为:1 6 5 4
最短路径对应的距离为:22
dist =
22
path =
1 6 5 4
两者结果一致,再次验证算法的有效性,而且自己写的Dijkstra算法的代码还能够一次输出所有点到终点的距离及路径表
仅一次测试以及少量的数据规模N不足以说明算法的解决效率,为了对两个算法性能进行一个比较,特地写了一个测试程序,输入的数据规模N从10到2000变化,并注释dijkstra.m、shortpath.m两个文件中的计时和输出结果部分的代码,程序如下
% 文件名:compar1.m
% 时间:2020年9月12日
% 来源:https://blog.csdn.net/lishan132/article/details/108527271
% 功能:比较自己实现的dijkstra算法与matlab图论工具箱函数的效率性能
% 说明:请先将dijkstra.m、shortpath.m文件与本文件放在同一目录下
clear
close
clc
iter = 200; %测试次数
t1 = zeros(1,iter); %算法1时间
t2 = zeros(1,iter); %算法2时间
for i = 1:iter
%% 第一步:生成测试数据,距离矩阵A,起点start,终点dest
clearvars -except iter i t1 t2 %清空除iter,i,t1,t2外的所有变量
N = i*10; %输入数据规模
ub = 15; %输入数据距离上限
A = unifrnd (0, ub, N, N); %生成一个服从均匀分布的矩阵,数值范围[0,ub],矩阵大小n×n
A = A - A';
A(A<0) = inf;
start = round(rand(1,1)*(N-1))+1;
dest = round(rand(1,1)*(N-1))+1;
while start == dest
dest = round(rand(1,1)*(N-1))+1;
end
%% 第二步:计算自己编写的dk算法的运行时间
tic %开始计时
dijkstra(A,start,dest);
t1(i) = toc; %计时结束
%% 第三步:计算使用matlab自带图论工具箱算法的运行时间
tic %开始计时
shortpath(A,start,dest);
t2(i) = toc; %计时结束
end
%% 第四步:绘制算法所需时间图
plot(1:iter,t1);
hold on
plot(1:iter,t2);
legend("文中dijkstra算法","图论工具shortestpath函数")
title("算法耗费时间比较")
惊喜地发现,随着数据规模的增大,自己写的Dijkstra算法与图论工具函数shortestpath相比,耗时更低,而且差距越来越大。
当然,此处还是有些不严谨,因为我在使用图论工具函数shortestpath解决问题时,前面自己还写了三条参数的处理语句,这部分语句的处理过程也是算入时间的
结论
本文实现了dijkstra算法的Matlab代码,并封装成一个函数,给定一个邻接矩阵,以及指定一个终点,可以直接输出任意点到终点的最短路径和相应的距离值,相对matlab自带的图论工具箱函数,其运算速度快,输出数据全,方便二次开发,提高效率。但自己写的程序中每次只寻找一个新的结点加入,有多少个结点,while中的循环体就要执行多少次,每一次循环均要更新一次所有结点到终点的距离值,当结点数据非常大时,时间复杂度为O(N^2),因此还有继续优化的空间,根据相关文献,可用堆进行优化,也可从能否一次加入多个新结点,而不是一个来考虑加快搜索速度。
参考文章:
[1] 数据结构--Dijkstra算法最清楚的讲解 https://blog.csdn.net/heroacool/article/details/51014824
[2] 通俗易懂理解——dijkstra算法求最短路径 https://zhuanlan.zhihu.com/p/40338107
[3] Dijkstra算法及其matlab实现 https://blog.csdn.net/u011317780/article/details/82429511
[4] 李建东,盛敏编著. 通信网络基础. 北京:高等教育出版社, 2004.08.
[5] 迪杰斯特拉 & 堆优化 https://blog.csdn.net/CSDNjiangshan/article/details/79345031