【预测模型】基于matlab模拟退火算法优化BP神经网络汇率预测【含Matlab源码 689期】

一、简介

1 模拟退火算法的应用背景
模拟退火算法提出于1982年。Kirkpatrick等人首先意识到固体退火过程与优化问题之间存在着类似性；Metropolis等人对固体在恒定温度下达到热平衡过程的模拟也给他们以启迪。通过把Metropolis 算法引入到优化过程中，最终得到一种对 Metropolis 算法进行迭代的优化算法，这种算法类似固体退火过程，称之为“模拟退火算法”。
模拟退火算法是一种适合求解大规模组合优化问题的随机搜索算法。目前，模拟退火算法在求解 TSP，VLSI 电路设计等组合优化问题上取得了令人满意的结果。将模拟退火算法同其它的计算智能方法相结合，应用到各类复杂系统的建模和优化问题中也得到了越来越多的重视，已经逐渐成为一种重要的发展方向。
2 模拟退火算法介绍




3 模拟退火算法的参数
模拟退火是一种优化算法，它本身是不能独立存在的，需要有一个应用场合，其中温度就是模拟退火需要优化的参数，如果它应用到了聚类分析中，那么就是说聚类分析中有某个或者某几个参数需要优化，而这个参数，或者参数集就是温度所代表的。它可以是某项指标，某项关联度，某个距离等等。

二、源代码

%% 基于模拟退火算法优化BP神经网络的汇率预测
clear all
clc
warning off
%% 导入数据
load exchange_rate.mat
x = [];
y = [];
tr_len =  800;
num_input = 10;
for i = 1:length(X)-num_input
    x = [x; X(i:i+num_input-1)];
    y = [y; X(i+num_input)];
end
%训练集——800个样本
input_train = x(1:tr_len, :)';
output_train = y(1:tr_len)';
%测试集——52个样本
input_test = x(tr_len+1:end, :)';
output_test = y(tr_len+1:end)';

%% BP网络设置
%节点个数
[inputnum,N]=size(input_train);%输入节点数量
outputnum=size(output_train,1);%输出节点数量

hiddennum=5;
%选连样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
%构建网络
net=newff(inputn,output_train,hiddennum);
%% SA算法参数初始化
nvar=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;
[outputn outputps]=mapminmax(output_train,0,1);% 归一化到【0 1】之间


%% SA算法主程序
lb=-1*ones(nvar,1); % 参数取值下界
ub=ones(nvar,1); % 参数取值上界
% 冷却表参数
MarkovLength=10; % 马可夫链长度
DecayScale=0.85; % 衰减参数
StepFactor=0.2; % Metropolis步长因子
Temperature0=8; % 初始温度
Temperatureend=3; % 最终温度
Boltzmann_con=1; % Boltzmann常数
AcceptPoints=0.0; % Metropolis过程中总接受点
% 随机初始化参数
range=ub-lb;
Par_cur=rand(size(lb)).*range+lb; % 用Par_cur表示当前解
Par_best_cur=Par_cur; % 用Par_best_cur表示当前最优解
Par_best=rand(size(lb)).*range+lb; % 用Par_best表示冷却中的最好解
% 每迭代一次退火(降温)一次，直到满足迭代条件为止
t=Temperature0;
itr_num=0; % 记录迭代次数
while t>Temperatureend
    itr_num=itr_num+1;
    itr_num
    t=DecayScale*t; % 温度更新（降温)
    for i=1:MarkovLength
        % 在此当前参数点附近随机选下一点
        p=0;
        while p==0
            Par_new=Par_cur+StepFactor.*range.*(rand(size(lb))-0.5);
            % 防止越界
            if sum(Par_new>ub)+sum(Par_new<lb)==0
                p=1;
            end
        end
        % 检验当前解是否为全局最优解
        if (objfun_BP(Par_best,inputnum,hiddennum,outputnum,net,inputn,outputn)>...
                objfun_BP(Par_new,inputnum,hiddennum,outputnum,net,inputn,outputn))
            % 保留上一个最优解
            Par_best_cur=Par_best;
            % 此为新的最优解
            Par_best=Par_new;
        end
        % Metropolis过程
        if (objfun_BP(Par_cur,inputnum,hiddennum,outputnum,net,inputn,outputn)-...
                objfun_BP(Par_new,inputnum,hiddennum,outputnum,net,inputn,outputn)>0)
            % 接受新解
            Par_cur=Par_new;
            AcceptPoints=AcceptPoints+1;
        else
            changer=-1*(objfun_BP(Par_new,inputnum,hiddennum,outputnum,net,inputn,outputn)...
                -objfun_BP(Par_cur,inputnum,hiddennum,outputnum,net,inputn,outputn))/Boltzmann_con*Temperature0;
            p1=exp(changer);
            if p1>rand
                Par_cur=Par_new;
                AcceptPoints=AcceptPoints+1;
            end
        end
    end
end
%% 结果显示
x=Par_best';
%% 把最优初始阀值权值赋予网络预测
% %用遗传算法优化的BP网络进行值预测
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);

net.iw{
     1,1}=reshape(w1,hiddennum,inputnum);
net.lw{
     2,1}=reshape(w2,outputnum,hiddennum);
net.b{
     1}=reshape(B1,hiddennum,1);
net.b{
     2}=B2;

%% BP网络训练
%网络进化参数
net.trainParam.epochs=100;
net.trainParam.lr=0.1;
net.trainParam.mc = 0.8;%动量系数，[0 1]之间
net.trainParam.goal=0.001;
%网络训练
net=train(net,inputn,outputn);
%网络训练
net=train(net,inputn,outputn);
%% BP训练集预测
BP_sim=sim(net,inputn);
%网络输出反归一化
T_sim=mapminmax('reverse',BP_sim,outputps);
% 
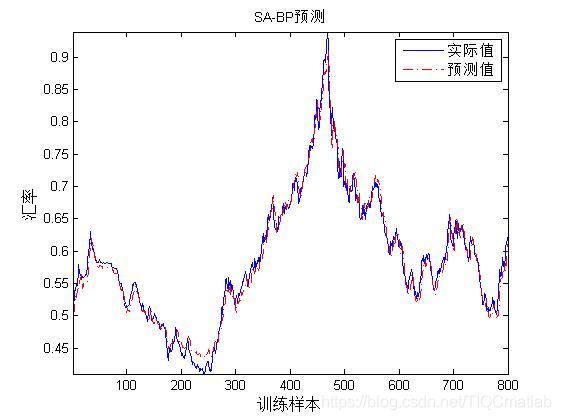
 figure
 plot(1:length(output_train),output_train,'b-','linewidth',1)
 hold on
 plot(1:length(T_sim),T_sim,'r-.','linewidth',1)
 axis tight
 xlabel('训练样本','FontSize',12);
 ylabel('汇率','FontSize',12);
 legend('实际值','预测值');
 string={
     'SA-BP预测'}
 title(string);
% %% 测试数据归一化
  inputn_test=mapminmax('apply',input_test,inputps);
% %预测输出
  an=sim(net,inputn_test);
  BPsim=mapminmax('reverse',an,outputps);
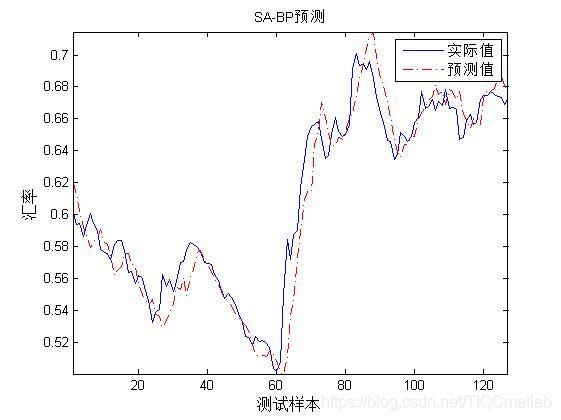
 figure
 plot(1:length(output_test), output_test,'b-','linewidth',1)
 hold on

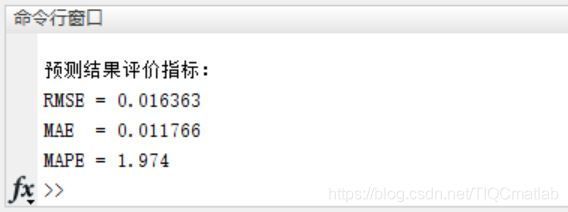
三、运行结果

四、备注

版本：2014a