二分查找

姓名：毛浩 学号：17029250003

【嵌牛导读】关于算法中十分常见的二分查找。

【嵌牛鼻子】二分查找

【嵌牛提问】二分查找基本思想和使用案例
【嵌牛正文】

二分查找是算法题中一种非常常见的基础算法。本文主要借鉴weiwei哥的个人算法书 —— 链接

---

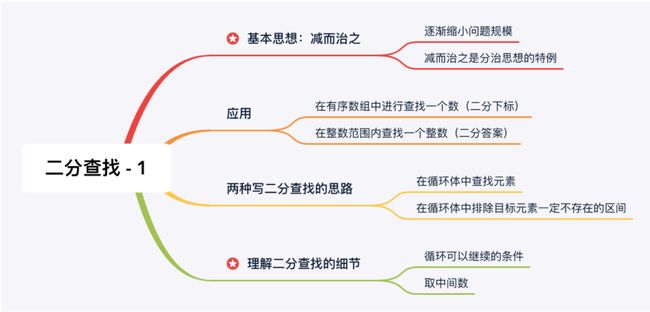
二分查找的基本思想：减而治之

二分查找的思想在我们的生活和工作中很常见，二分查找通过不断缩小搜索区间的范围，直到找到目标元素或者没有找到目标元素。这里不断缩小搜索区间是一种 减而治之 的思想，也称为减治思想。

1605062779533.png

「减而治之」思想简介

这里「减」是「减少问题」规模的意思，治是「解决」的意思。「减治思想」从另一个角度说，是「排除法」，意即：每一轮排除掉一定不存在目标元素的区间，在剩下可能存在目标元素的区间里继续查找。每一次我们通过一些判断和操作，使得问题的规模逐渐减少。又由于问题的规模是有限的，我们通过有限次的操作，一定可以解决这个问题。

可能有的朋友听说过「分治思想」，「分治思想」与「减治思想」的差别就在于，我们把一个问题拆分成若干个子问题以后，应用「减治思想」解决的问题就只在其中一个子问题里寻找答案。「分治思想」我们在下一章会向大家介绍。

• 例 1：以前央视二套的《幸运 52》栏目有一个「猜价格」游戏。游戏规则是：给出一个商品，告诉答题者它的价格在多少元（价格为整数）以内，让答题者猜，如果猜出的价格低于真正价格，主持人就说少了，高于真正的价格，就说多了，看谁能在最短的时间内猜中。这个游戏就是应用减治思想完成「猜价格」任务的。主持人说「多了」或这「少了」，就是给参与游戏的人反馈，让游戏者逐渐缩小价格区间，最终猜中价格。

• 例 2：不知道大家小时候查《新华字典》的时候是怎么查的，我经常不翻目录，直接根据要找的字的拼音，在字典里翻页。例如要找的字是「算」（汉语拼音首字母为 S），如果一开始翻到了 L 开头的页，那么我就会在 L 开头的页后面的页里任意挑一页。如果看到的是 T 开头的页，我就会在 T 开头的页前面的页里任意挑一页，这样的查字典的策略就应用了减治思想。

• 例 3：相信有不少程序员定位程序中的 bug 的时候，会在程序里打印一些变量的输出语句，逐步定位有问题的代码的行，这样的定位问题的方法也应用了「减治思想」。

二分查找算法的应用范围

在有序数组中进行查找一个数（二分下标）

这里「数组」和「有序」是很重要的，我们知道：数组具有 随机访问 的特性，由于数组在内存中 连续存放，因此我们可以通过数组的下标快速地访问到这个元素。如果数据存放在链表中，访问一个元素我们都得通过遍历，有遍历的功夫我们早就找到了这个元素，因此，在链表中不适合使用二分查找。

在整数范围内查找一个整数（二分答案）

如果我们要找的是一个整数，并且我们知道这个整数的范围，那么我们就可以使用二分查找算法，逐渐缩小整数的范围。这一点其实也不难理解，假设我们要找的数最小值为 00，最大值为 NN，我们就可以把这个整数想象成数组 [0, 1, 2,..., N] 里的一个值，这个数组的下标和值是一样的，找数组的下标就等于找数组的值。这种二分法用于查找一个有范围的数，也被称为「二分答案」，或者「二分结果」，也就是在「答案区间」里或者是「结果区间」里逐渐缩小目标元素的范围；

在我们做完一些问题以后，我们就会发现，其实二分查找不一定要求目标元素所在的区间是有序数组，也就是说「有序」这个条件可以放宽，半有序数组或者是山脉数组里都可以应用二分查找算法。

旋转数组和山脉数组有什么样的特点呢？可以通过当前元素附近的值推测出当前元素一侧的所有元素的性质，也就是说，旋转和山脉数组的值都有规律可循，元素的值不是随机出现的，在这个特点下，「减治思想」就可以应用在旋转数组和山脉数组里的一些问题上。我们可以把这两类数组统一归纳为部分有序数组。

二分查找算法的两种思路

• 思路 1：在循环体中查找元素
• 思路 2：在循环体中排除目标元素一定不存在的区间

二分查找的最基本问题

最基础的二分查找的问题就是在一个有序数组中查找目标元素

思路1

代码块

class Solution {
public:
    int search(vector& nums, int target) {
        int l = 0, r = nums.size() - 1;
        while(l <= r){
            int m = l + (r - l) / 2;
            if(nums[m] == target)   return m;
            else if(nums[m] < target)   l = m + 1;
            else r = m - 1;
        }
        return -1;
    }
};

思路2

1605065500626.png

在这一节内容的一开始，我们先来看一下，「力扣」第 704 题另外两种「二分查找」的写法，事实上这两种写法在思想上是一样的。

代码块1

class Solution {
public:
    int search(vector& nums, int target) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] < target)   l = m + 1;
            else r = m;
        }
        return nums[l] == target ? l : -1;
    }
};

代码块2

class Solution {
public:
    int search(vector& nums, int target) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l + 1) / 2;
            if(nums[m] > target)   r = m - 1;
            else l = m;
        }
        return nums[l] == target ? l : -1;
    }
};

我们看一下，这两种写法和思路 1 的写法有何不同。

循环可以继续的条件是 while (left < right) ，这是一个很重要的标志。为什么是严格小于呢？我们上一节说过，当 left == right ，左边界和右边界重合的时候，区间里只有 1 个元素时候，二分查找的逻辑还需要继续下去；而现在大家看到的这个解法在 left == right 重合的时候就退出了循环，这一点表示区间里只剩下一个元素的时候，有可能这个元素就是我们要找的那个元素。这一点与二分查找算法的思路 2（在循环体中排除元素）是一致的：排除了所有错误的答案，如果题目告诉我们只有 11 个目标元素，那么剩下的这个元素就一定是目标元素。
在退出循环以后，还需要单独做一次判断；那么这样的写法是不是更麻烦了呢？其实不是的：

• 首先，有些算法问题根据题目的意思，要找的目标元素一定落在题目给的区间里，那么最后的这一步判断可以省略；
• 并且我们看到这个写法只把区间分成了两个部分，其实在我们编写代码的时候要考虑的因素会更少。这两个区间没有交集，并且它们合起来组成了整个当前待搜索的区间。因此，在思考缩小待搜索区间的逻辑的时候，只需要考虑其中一种情况，另一种情况得到的区间就正好是上一个区间的反面区间；
• 那么如何考虑缩小问题的区间呢？通常的思路是：先思考要找的数的性质，然后对这个性质取反，也就是：先讨论看到的中间位置的元素在什么情况下不是目标元素，采用这样的思路解决问题会容易一些；

友情提示：生活中的一些事情我们往往很清楚自己不需要什么，但是说不清楚自己真正需要什么。从中间位置的元素在什么情况下不是目标元素考虑，使得问题变得简单也是类似的事实。

适用范围

• 如果这个二分查找的问题比较简单，在输入数组里不同元素的个数只有 1 个，使用思路 1 ，在循环体内查找这个元素；
• 如果这个二分查找的问题比较复杂，要你找一个可能在数组里不存在，或者是找边界这样的问题，使用思路 2 ，在循环体内排除一定不存在目标元素的区间会更简单一些。

二分查找的细节（重点）

细节 1：循环可以继续的条件

while (left <= right) 表示在区间里只剩下一个元素的时候，我们还需要继续查找，因此循环可以继续的条件是 left <= right，这一行代码对应了二分查找算法的思路 1：在循环体中查找元素。

细节 2：取中间数的代码

取中间数的代码 int mid = (left + right) / 2; ，严格意义上是有 bug 的，这是因为在 left 和 right 很大的时候，left + right 有可能会发生整型溢出，这个时候推荐的写法是：

int m = l + (r - l) / 2;

细节 3：取中间数可不可以上取整

我们在「细节 2」里介绍了 int mid = (left + right) / 2; 这个表达示里 / 2 这个除号表示的含义是下取整。很显然，在区间里有偶数个元素的时候位于中间的数有 22 个，这个表达式只能取到位于左边的那个数。一个很自然的想法是，可不可以取右边呢？

int m = l + (r - l + 1) / 2;

编码要点

• 循环终止条件写成：while (left < right) ，表示退出循环的时候只剩下一个元素；
• 在循环体内考虑如何缩减待搜索区间，也可以认为是在待搜索区间里排除一定不存在目标元素的区间；
• 根据中间数被分到左边和右边区间，来调整取中间数的行为；
• 如何缩小待搜索区间，一个有效的办法是：从 nums[mid] 满足什么条件的时候一定不是目标元素去考虑，进而考虑 mid 的左边元素和右边元素哪一边可能存在目标元素。一个结论是：当看到 left = mid 的时候，取中间数需要上取整，这一点是为了避免死循环；
• 退出循环的时候，根据题意看是否需要单独判断最后剩下的那个数是不是目标元素。

边界设置的两种写法：

• right = mid 和 left = mid + 1 和 int mid = left + (right - left) / 2; 一定是配对出现的；
• right = mid - 1 和 left = mid 和 int mid = left + (right - left + 1) / 2; 一定是配对出现的。

经典题目

34题：

这道题主要利用思路2来排除不符合的区间，通过两个函数分别找到左右端。

代码

class Solution {
public:
    vector searchRange(vector& nums, int target) {
        if(nums.empty())    return {-1, -1};
        int l = searchLeft(nums, target);
        if(l == -1) return {-1, -1};//一个编码小细节，如果找不到左端说明这个数不存在可直接返回
        int r = searchRight(nums, target);
        return {l, r};
    }
    int searchLeft(vector& nums, int target){
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] < target)    l = m + 1;
            else r = m;
        }
        return nums[l] == target ? l : -1;
    }
    int searchRight(vector& nums, int target){
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l + 1) / 2;
            if(nums[m] > target)    r = m - 1;
            else l = m;
        }
        return nums[l] == target ? l : -1;
    }
};

35题

1605182078678.png

这道题非常简单，还是思路2排除比target小的区间即可（注意特殊情况当target大于数组最大值）

代码

class Solution {
public:
    int searchInsert(vector& nums, int target) {
        int n = nums.size();
        if(!n)    return 0;
        if(target > nums[n-1])  return n;
        int l = 0, r = n - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] < target)    l = m + 1;
            else    r = m;
        }
        return l;
    }
};

36题

1605512459012.png

这道题所给的数组并不是一个严格意义上的排序数组，它是在排序数组的基础上进行了部分旋转。
我们可以根据旋转后数组的中间数和左右端的数进行比较，从而确定最小值处在左边还是右边。

• nums[mid] > nums[left], nums[right] > nums[mid]. 这种情况属于未进行旋转的原始排序数组。最小值位于左半边，收缩右边界。
• nums[mid] > nums[left], nums[right] < nums[mid] 最小值位于右半边，收缩左边界。
• nums[mid] < nums[left], nums[right] > nums[mid] 这种单调递减的情况不存在。
• nums[mid] < nums[left], nums[right] < nums[mid] 最小值位于左半边，收缩右边界。
  根据以上分析，我们可以看到判断收缩左边界还是右边界可以利用中间值和最右值的大小比较。

代码

class Solution {
public:
    int findMin(vector& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] < nums[r]){
                r = m;
            }
            else{
                l = m + 1;
            }
        }
        return nums[l];
    }
};

154题

1605513997240.png

这道题在上一道题的基础上引入了可重复这一条件。因此在比较中间值和最右值的大小时，有可能出现相等的情况。在这种情况下，最小值既可能出现在左半边也可能出现在右半边。倘若最右值即是最小值，那么因为中间值和最右值不是同一个位置，因此在中间到最右这个区间内均为最小值，此时我们可以收缩右边界一个单位。最右值如果不是最小值，那可以直接收缩右边界一个单位。

代码

class Solution {
public:
    int findMin(vector& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            if(nums[m] < nums[r])   r = m;
            else if(nums[m] > nums[r])  l = m + 1;
            else    r -= 1;
        }
        return nums[l];
    }
};

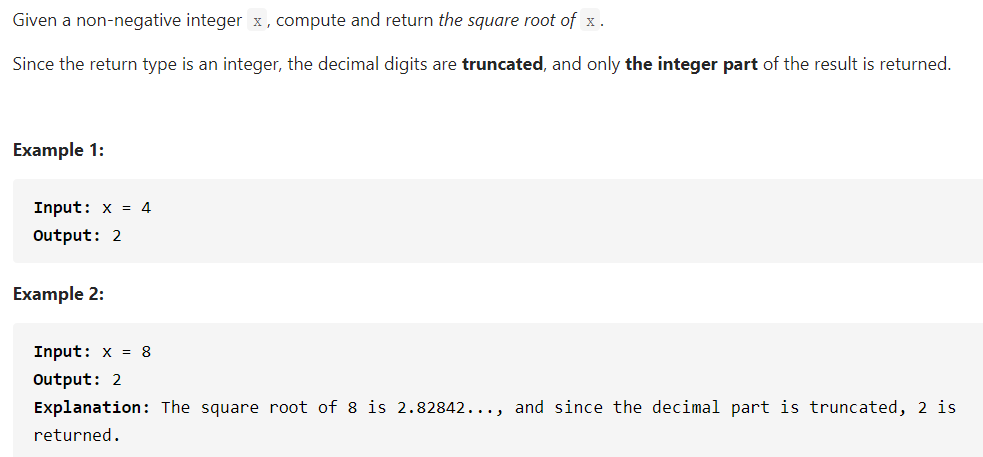
69题

1605749379248.png

这道题就是一个很基础的实现sqrt()函数的内容。
我们知道任何一个自然数的平方根都不可能大于其一半，因此右边界可以从该数的一半开始。

代码

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x / 2 + 1;//针对特殊情况1
        while(l < r){
            long m = l + (r - l + 1) / 2;//防止数过大超过整型
            long tmp = m * m;
            if(tmp > x) r = m - 1;
            else l = m;
        }
        return l;
    }
};

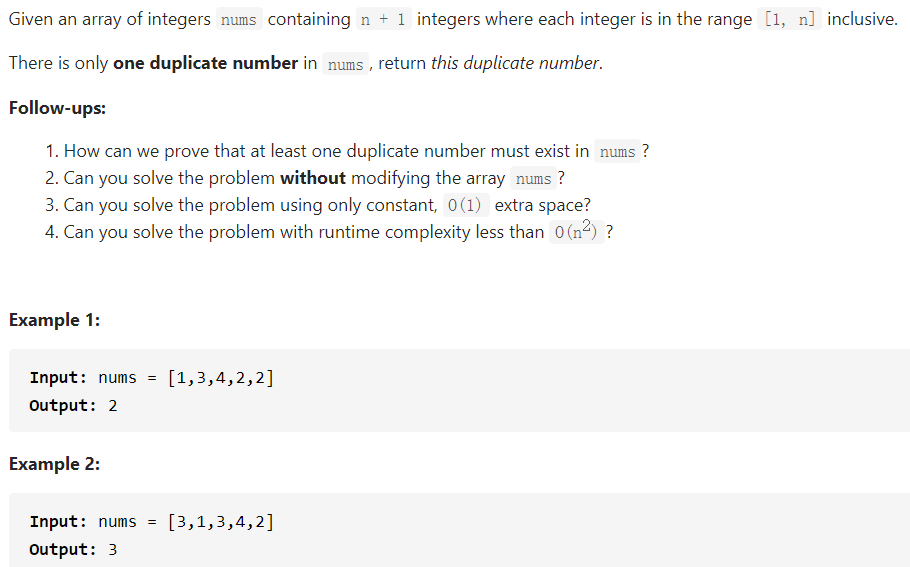
287题

1605751095213.png

这道题可以用二分法我是没想到的，看了weiwei哥的题解后感到十分惊艳。我们用二分法时，要注意思考我们二分什么内容，找到了这个关键点，题目也就水落石出了，当然这个key得根据题意来判断。
这道题我们可以通过找小于等于中间值的个数来判断收缩哪个区间。

代码

class Solution {
public:
    int findDuplicate(vector& nums) {
        int n = nums.size();
        int l = 1, r = n - 1;
        while(l < r){
            int m = l + (r - l) / 2;
            int cnt = 0;
            for(int i=0; i m) r = m;
            else l = m + 1;
        }
        return l;
    }
};