【基础算法】第二章 贪心算法
例一 奶牛晒衣服
题目描述
有n件衣服,第i件衣服的湿度为h。
在自然条件下,每件衣服每分钟都可以自然晒干A点湿度。
在烘干机作用下,可以选择一件衣服,用一分钟的时间晒干B点湿度。
求出晒干所有衣服的最少时间(湿度为0为干)。
输入格式
第一行三个正整数N,A,B。
接下来N行,第i行一个正整数,表示第i件衣服的湿度
h。
输出格式
输出一个数,表示晒干所有衣服的最少时间。
样例输入
3 2 1
1
2
3
样例输出
1
分析
在不考虑烘干机的情况下,最后一件烘干的衣服一定是湿度最大的衣服,所以我们希望湿度最大的衣服的湿度越小越好。
所以得到:让湿度最大的衣服使用烘干机。
Code:
#include
using namespace std;
priority_queue pq;
int n,A,B;
int t;
int main()
{
cin>>n>>A>>B;
for (int i=1;i<=n;i++) {
int x;
cin>>x;
pq.push(x);
}
while(1){
++t;
int x=pq.top();
pq.pop();
x-=B;
pq.push(x);
if (pq.top()-t*A<=0) {
cout< 例二 雷达装置
题目描述
有n个建筑物,第i个建筑物在笛卡尔坐标系上的坐标为(x,y),你需要在x轴上安装一些雷达,每个雷达的侦察半径均为d,要求每个建筑物都至少被一个雷达侦测到,求最少要安装几个雷达。
输入格式
第一行两个正整数n,d。
接下来n行,第i行两个整数x,y。
输出格式
输出一行表示答案,若没有解决方案,则答案为-1。
样例输入
3 2
1 2
-3 1
2 1
样例输出
2
分析
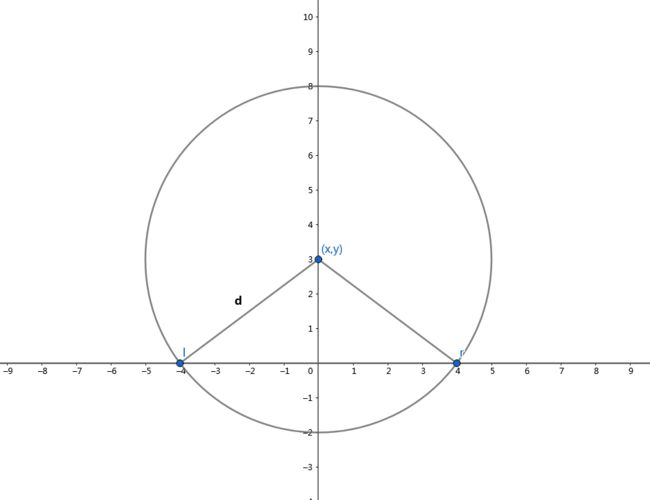
如图,将所有建筑物转化成雷达建造区间
1.将所有区间按右端点从小到大排序。
2.依次考虑每一个区间:
·若当前区间内包含最后一个选择的点,则直接跳过。
·若当前区间内不包含最后一个选择的点,则在该区间的右端点放一个新点。
Code:
#include
using namespace std;
int n,d,x,y,s=1;
double tail;
struct node
{
double l,r;
}a[1005];
bool cmp(node x,node y)
{
return x.r>n>>d;
for(int i=1;i<=n;i++)
{
cin>>x>>y;
if(dtail){
s++;
tail=a[i].r;
}
cout< 例三 畜栏预定
题目描述
有N头牛在畜栏中吃草。每个畜栏在同一时间段只能提供给一头牛吃草,所以可能会需要多个畜栏,给出第i头牛开始吃草的时间区间[A,B],求需要的最少畜栏数和每头牛对应的畜栏方案。
输入格式
第一行一个正整数N。
接下来N行,第i行两个正整数A,B。
输出格式
第一行一个整数,表示需要的最少畜栏数。
接下来N行,第i行一个整数表示第i头牛的对应畜栏,编号是从1开始的连续整数,方案合法即可。
样例输入
5
1 10
2 4
3 6
5 8
4 7
样例输出
4
1
2
3
2
4
分析
1.将牛按开始吃草的时间排序。
2.维护每个畜栏安排进去的最后的一头牛,依次考虑每一头牛,找到满足“当前的牛开始吃草的时间不早于畜栏中最后的一头牛结束吃草的时间”的任意的一个畜栏,将其安排进去,若没有这样的畜栏,则为其新建一个畜栏。
Code
#include
using namespace std;
int n;
int a[100000][3];
int ans[100000];
struct node{
int x, y;
}s[100000];
bool cmp(node x,node y){
return x.x>n;
int m=0;
for(int i=1; i<=n; i++)
cin>>s[i].x>>s[i].y;
sort(s+1, s+n+1, cmp);
for(int i=1; i<=n; i++){
int x, y, flag=0;
x=s[i].x, y=s[i].y;
for(int j=1; j<=m; j++){
if(a[j][2] 例四 荷马史诗
洛谷P2168
题目背景
追逐影子的人,自己就是影子 —— 荷马
题目描述
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 n 种不同的单词,从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。Allison 想要用 k 进制串 si 来替换第 i 种单词,使得其满足如下要求:
对于任意的 1≤i,j≤n,i!=j,都有:si不是 sj的前缀。
现在 Allison 想要知道,如何选择 si,才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的 si 的最短长度是多少?
一个字符串被称为 k 进制字符串,当且仅当它的每个字符是 0 到 k−1之间(包括 0 和 k−1 )的整数。
字符串 str1 被称为字符串 str2 的前缀,当且仅当:存在 1≤t≤m ,使得 str1=str2[1..t]。其中,m 是字符串 str2 的长度,str2[1..t] 表示 str2 的前 t 个字符组成的字符串。
输入格式
输入的第 1 行包含 2 个正整数 n,k,中间用单个空格隔开,表示共有 n 种单词,需要使用 k 进制字符串进行替换。
接下来 n 行,第 i+1 行包含 1 个非负整数 wi,表示第 i 种单词的出现次数。
输出格式
输出包括 2 行。
第 1 行输出 1 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 2 行输出 1 个整数,为保证最短总长度的情况下,最长字符串 si 的最短长度。
样例输入 1
4 2
1
1
2
2
样例输出 1
12
2
样例输入 2
6 3
1
1
3
3
9
9
样例输出 2
36
3
