逼近理想解法TOPSIS(python程序)

逼近理想解排序法，也称优劣解距离法，是多目标决策分析中一种常用的距离综合评价方法。基本思想是定义决策问题的理想解和负理想解，根据有限个评价对象与理想解的接近程度进行排序，找到最优方案。
正负理想解是一个方案集中并不存在的虚拟最佳、最劣方案。它的每个属性值都是决策矩阵中该属性的最好的值、最坏的值。将每个方案分别与最优、最劣理想解计算欧式距离，并进一步可计算出对方案的最终排序。
基本步骤：

1. 确定指标体系，构造评估矩阵。
2. 无量纲化评估矩阵。
3. 构造加权评估矩阵（可有可无）。
4. 确定正理想解、负理想解。
5. 计算各评价对象到正理想解和负理想解的距离。
6. 计算各方案最终排序。

1.评估矩阵为:

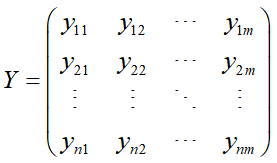
2.无量纲评估矩阵：
使用如下公式：

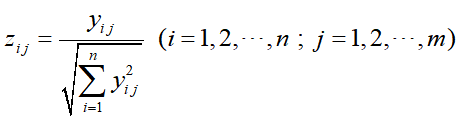
得到无量纲化后的评估矩阵为：

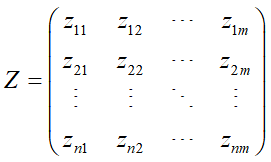
3.构造加权评估矩阵：若指标间的重要程度不同，给不同指标赋予不同的权重。指标权重构成的向量表示为：

加权评估矩阵为：



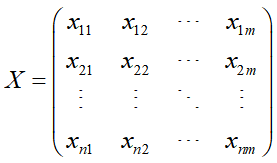
4.确定正理想解、负理想解：
.效益型指标，指这个指标的数值越大越好。成本型指指标数值越小越好。正理想解为：

负理想解为：

最终的正、负理想解分别为：

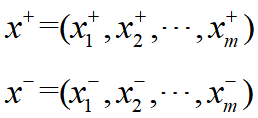
5.计算各评价对象到正、负理想解的欧式距离：
各评价对象到正理想解的距离：

到负理想解的距离：

6. 各评价目标的综合评价指数：

Ci越大，该评价目标得分越高，越好

python程序如下：

data=np.array([[4.0,0.074 , 88.0, 2.0, 0.69, 20.0, 1.0], #方案1
                   [5.0, 0.07 ,  85.0, 3.0, 0.69, 30.0, 3.0], #方案2
                   [6.0, 1.13  , 85.0, 2.0, 0.28, 200.0, 17.0],#方案3
                   [3.0, 8.04   ,88.0, 2.0, 1.53 ,189.8, 5.0], ##方案4
                   [2  , 9.45  , 86  , 3  , 1.92, 120 ,8],     ##方案5
                   [1  , 8.17 ,  88  , 3  , 0.69, 180, 14],   ##方案6
                   [7  , 12.6  , 88  , 1  , 0.26, 162, 13]])  ##方案7

##共7个评价目标/方案/对象，每个方案8个指标，第1、2、6、7为成本型指标，第3、4、5为效益型指标。

def jisuan(data): #确定最优、最劣理想解分别为maxl,minl
    maxl=[]
    minl=[]
    for i in range(0,2):   ###第
        maxl.append(np.min(data[:,i]))
        minl.append(np.max(data[:,i]))
    for i in range(2,5):
        maxl.append(np.max(data[:,i]))
        minl.append(np.min(data[:,i]))
    for i in range(5,7):
        maxl.append(np.min(data[:,i]))
        minl.append(np.max(data[:,i]))
    return maxl,minl


def D(maxl,minl,data): #计算到每个方案到最优、最劣理想解的距离，分别为D_jia,D_jian
    D_jia=[]
    D_jian=[]
    for i in range(0,7):
        a=np.square(data[i,0]-maxl[0])+np.square(data[i,1]-maxl[1])+np.square(data[i,2]-maxl[2])+np.square(data[i,3]-maxl[3])+np.square(data[i,4]-maxl[4])+np.square(data[i,5]-maxl[5])+np.square(data[i,6]-maxl[6])
        a=np.sqrt(a)
        D_jia.append(a)
        b=np.square(data[i,0]-minl[0])+np.square(data[i,1]-minl[1])+np.square(data[i,2]-minl[2])+np.square(data[i,3]-minl[3])+np.square(data[i,4]-minl[4])+np.square(data[i,5]-minl[5])++np.square(data[i,6]-minl[6])
        b=np.sqrt(b)
        D_jian.append(b)
    return D_jia,D_jian

def biaozhunhua(data): #标准化处理
    data_biaozhun=np.zeros([7,7])
    print(data_biaozhun)
    for i in range(0,7):     #列
        for j in range(0,7): #行
           data_biaozhun[j,i]=(data[j,i]-np.min(data[:,i]))/(np.max(data[:,i])-np.min(data[:,i]))
    return data_biaozhun

#print(data_600s.dtype)
data_xin=biaozhunhua(data) #先无量纲化
print("标准化后",data_xin)
#print("标准化后",biaozhun_75)
maxl,minl=jisuan(data_xin)##计算最优、最劣理想解
print(maxl)
print(minl)
D_jia,D_jian=D(maxl,minl,data_xin) #计算每个方案到最优、最劣理想解的距离
print('正理想解',D_jia)
print('负理想解',D_jian)
a=0
for i in range(0,7):  
    a=a+(D_jian[i]/(D_jian[i]+D_jia[i]))
    print(D_jian[i]/(D_jian[i]+D_jia[i])) ##输出的是最后每个方案综合得分
print('归一化得分为：')
for i in range(0,7):
    print((D_jian[i]/(D_jian[i]+D_jia[i]))/a)##输出的是每个方案综合得分归一化后的数值。