RF2O激光里程计算法原理
参考论文:Planar Odometry from a Radial Laser Scanner. A Range Flow-based Approach
RF2O根据传感器速度制定范围流约束方程,并最小化所得几何约束的鲁棒函数以获得运动估计。

设 R ( t , α ) R(t,α) R(t,α)为范围扫描,其中 t t t是时间, α ∈ [ 0 , N ) ⊂ R α \in [0,N)⊂R α∈[0,N)⊂R是扫描坐标,N是扫描的大小。 任何点P相对于连接到传感器的局部参考系的位置由其极坐标 ( r , θ ) (r,θ) (r,θ)给出,如果从激光雷达扫描点P,则 a a a如下所示,其中FOV为扫描仪的视野:
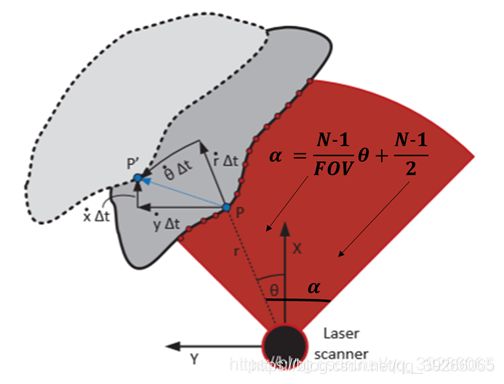
设 k a = N − 1 F O V k_a = {N-1 \over FOV} ka=FOVN−1,则公式(1)为:
a = N − 1 F O V θ + N − 1 2 = k a θ + N − 1 2 a = {N-1 \over FOV} \theta + {N-1 \over 2} = k_a \theta+{N-1 \over 2} a=FOVN−1θ+2N−1=kaθ+2N−1
假设 R R R是可微的,则在第二次扫描的中,每个点的范围可以表达成泰勒展开式(公式2):
R ( t + Δ t , a + Δ a ) = R ( t , a ) + ∂ R ∂ t ( t , a ) Δ t + ∂ R ∂ a ( t , a ) Δ a + O ( Δ t 2 , Δ a 2 ) R(t+\Delta t,a+ \Delta a) = R(t,a)+{∂R \over ∂t}(t,a)\Delta t + {∂R \over ∂a}(t,a)\Delta a +O(\Delta t^2, \Delta a^2) R(t+Δt,a+Δa)=R(t,a)+∂t∂R(t,a)Δt+∂a∂R(t,a)Δa+O(Δt2,Δa2)其中 Δ t \Delta t Δt是连续扫描之间的时间间隔, Δ a \Delta a Δa表示所考虑的点的扫描坐标的变化。
忽略二阶/高阶项,设: Δ R = R ( t + Δ t , a + Δ a ) − R ( t , a ) , R t = ∂ R ∂ t ( t , a ) , R a = ∂ R ∂ a ( t , a ) \Delta R = R(t+\Delta t,a+\Delta a) - R(t,a),R_t={∂R \over ∂t}(t,a),R_a = {∂R \over ∂a}(t,a) ΔR=R(t+Δt,a+Δa)−R(t,a),Rt=∂t∂R(t,a),Ra=∂a∂R(t,a)将扫描梯度与区间 [ t , t + Δ t ] [t,t +Δt] [t,t+Δt]期间点的范围和扫描坐标的变化联系起来,则公式(2)化简如下: Δ R ≈ R t Δ t + R a Δ a \Delta R \approx R_t \Delta t + R_a \Delta a ΔR≈RtΔt+RaΔa同时除以 Δ t \Delta t Δt得到: Δ R Δ t ≈ R t + R a Δ a Δ t {\Delta R \over \Delta t} \approx R_t+ R_a {\Delta a \over \Delta t} ΔtΔR≈Rt+RaΔtΔa
假设 r ˊ = Δ R Δ t \acute{r} = {\Delta R \over \Delta t} rˊ=ΔtΔR, a ˊ = Δ a Δ t \acute{a}={\Delta a \over \Delta t} aˊ=ΔtΔa,在区间 [ t , t + Δ t ] [t,t +Δt] [t,t+Δt]内,扫描点范围和扫描坐标的平均速度!因此可以得到(公式4)(range flow constraint equation): Δ R Δ t ≈ R t + R a Δ a Δ t ⟹ r ˊ ≈ R t + R a a ˊ = R t + R a k a θ ˊ {\Delta R \over \Delta t} \approx R_t+ R_a {\Delta a \over \Delta t} \implies \acute{r} \approx R_t+ R_a\acute{a} =R_t+ R_ak_a \acute{\theta} ΔtΔR≈Rt+RaΔtΔa⟹rˊ≈Rt+Raaˊ=Rt+Rakaθˊ
为了描述所有点在相同的向量基下的速度,我们将径向和方位角速度 ( r ˊ , θ ˊ ) (\acute{r},\acute{\theta}) (rˊ,θˊ)转换为笛卡尔表示 ( x ˊ , y ˊ ) (\acute{x},\acute{y}) (xˊ,yˊ),如上图所示,可得到: r ˊ = x ˊ c o s θ + y ˊ s i n θ \acute{r}=\acute{x}cos\theta + \acute{y}sin\theta rˊ=xˊcosθ+yˊsinθ同理: r θ ˊ = y ˊ c o s θ − x ˊ s i n θ r\acute{\theta}=\acute{y}cos\theta - \acute{x}sin\theta rθˊ=yˊcosθ−xˊsinθ
强制每个明显的运动都是由于激光雷达平移或加上旋转所引起的,即假设每个点都相对于传感器移动,好像它是刚体的一部分,其速度相同但与传感器的符号相反,即: ( x ˊ y ˊ ) = ( − v x , s + y ω s − v y , s − x ω s ) \begin{pmatrix} \acute{x} \\ \acute{y} \\ \end{pmatrix} = \begin{pmatrix} -v_{x,s}+y\omega_s \\ -v_{y,s}-x\omega_s\\ \end{pmatrix} (xˊyˊ)=(−vx,s+yωs−vy,s−xωs)
将转换后的笛卡尔速度代入到公式4中,可以推导得到:
r ˊ ≈ R t + R a k a θ ˊ ⟹ x ˊ c o s θ + y ˊ s i n θ ≈ R t + R a k a y ˊ c o s θ − x ˊ s i n θ r \acute{r} \approx R_t+ R_ak_a \acute{\theta} \implies \acute{x}cos\theta + \acute{y}sin\theta \approx R_t+ R_ak_a {\acute{y}cos\theta - \acute{x}sin\theta \over r} rˊ≈Rt+Rakaθˊ⟹xˊcosθ+yˊsinθ≈Rt+Rakaryˊcosθ−xˊsinθ即: x ˊ ( c o s θ + R a k a s i n θ r ) + y ˊ ( s i n θ − R a k a c o s θ r ) − R t = 0 \acute{x}(cos\theta+{ R_ak_a sin\theta \over r}) + \acute{y}(sin\theta-{R_ak_a cos\theta \over r}) - R_t=0 xˊ(cosθ+rRakasinθ)+yˊ(sinθ−rRakacosθ)−Rt=0再加上刚才的假设: ( − v x , s + y ω s ) ( c o s θ + R a k a s i n θ r ) + ( − v y , s − x ω s ) ( s i n θ − R a k a c o s θ r ) − R t = 0 ( -v_{x,s}+y\omega_s)(cos\theta+{ R_ak_a sin\theta \over r}) + ( -v_{y,s}-x\omega_s)(sin\theta-{R_ak_a cos\theta \over r}) - R_t=0 (−vx,s+yωs)(cosθ+rRakasinθ)+(−vy,s−xωs)(sinθ−rRakacosθ)−Rt=0 ⟹ v x , s ( c o s θ + R a k a s i n θ r ) + v y , s ( s i n θ − R a k a c o s θ r ) + ω s ( x s i n θ − y c o s θ − R a k a ( c o s θ x + s i n θ y r ) ) + R t = 0 \implies v_{x,s}(cos\theta+{ R_ak_a sin\theta \over r}) + v_{y,s}(sin\theta-{R_ak_a cos\theta \over r})+ \omega_s(xsin\theta - ycos\theta - R_ak_a ({cos\theta x+sin\theta y \over r}))+R_t=0 ⟹vx,s(cosθ+rRakasinθ)+vy,s(sinθ−rRakacosθ)+ωs(xsinθ−ycosθ−Raka(rcosθx+sinθy))+Rt=0又因为 r = c o s θ x + s i n θ y r=cos\theta x+sin\theta y r=cosθx+sinθy
因此最终化简得到: v x , s ( c o s θ + R a k a s i n θ r ) + v y , s ( s i n θ − R a k a c o s θ r ) + ω s ( x s i n θ − y c o s θ − R a k a ) + R t = 0 v_{x,s}(cos\theta+{ R_ak_a sin\theta \over r}) + v_{y,s}(sin\theta-{R_ak_a cos\theta \over r})+ \omega_s(xsin\theta - ycos\theta - R_ak_a)+R_t=0 vx,s(cosθ+rRakasinθ)+vy,s(sinθ−rRakacosθ)+ωs(xsinθ−ycosθ−Raka)+Rt=0
总得来说,每个扫描点对传感器运动都施加了限制,因此,3个线性独立的限制在理论上足以估计它。
