凸优化理论基础2——凸集和锥
作者简介:秃头小苏,致力于用最通俗的语言描述问题
往期回顾:凸优化理论基础1–仿射集
近期目标:拥有5000粉丝
支持小苏:点赞、收藏⭐、留言
文章目录
- 凸优化理论基础2——凸集和锥
-
- 凸集
- 凸组合
- 凸包
- 锥和凸锥
- 锥组合
- 锥包
- 重要例子
- 凸集、凸锥、仿射集三者关系图
凸优化理论基础2——凸集和锥
之前我已经介绍过仿射集的概念了,自认为讲的还算清楚,阅读此篇文章前建议先了解仿射集的相关概念
凸集
- 定义
定义: 集合C为凸集等价为 ⇔ \Leftrightarrow ⇔C中任意两点间的线段仍然在C中,即对任意的 x 1 , x 2 ∈ C x_1,x_2 \in C x1,x2∈C 和满足 0 ≤ θ ≤ 1 0 \le \theta \le 1 0≤θ≤1 都有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1 +(1- \theta)x_2 \in C θx1+(1−θ)x2∈C。
我们在学习相关概念的时候一定要学会对比着学习,凸集从概念上和仿射集是非常相近的,仿射集要求C中任意两点的直线仍然在C中,而凸集只需要求任意两点间的线段仍然在C中,也即凸集对 θ \theta θ有一定的限制。从这个定义的差别来看,其实我们就能够得到一个结论:仿射集一定是凸集。
- 例子
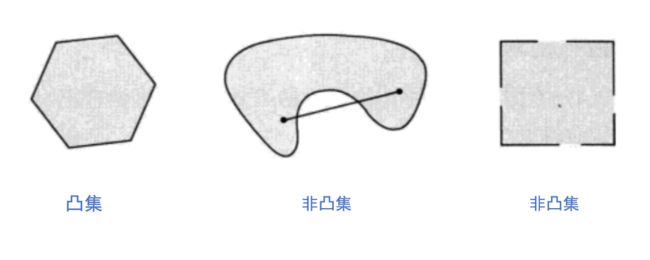
凸集我认为是非常容易理解的,下面的三个例子根据凸集的定义也很好判断是否为凸集
凸组合
和仿射组合的概念类似,我们称 θ 1 x 1 + ⋯ + θ k x k \theta_1x_1 + \cdots +\theta_kx_k θ1x1+⋯+θkxk 为点 x 1 , ⋯ , x k x_1 , \cdots ,x_k x1,⋯,xk 的一个凸组合。其中 θ 1 + ⋯ + θ k = 1 \theta_1 + \cdots +\theta_k=1 θ1+⋯+θk=1 且 θ i ≥ 0 , i = 1 , ⋯ , k \theta _i \ge 0 ,i=1, \cdots ,k θi≥0,i=1,⋯,k。同样的,类似于仿射组合,一个集合是凸集合等价于集合包含其中所有点的凸组合。【注意:这里的 θ i ≥ 0 \theta _i \ge 0 θi≥0是凸组合所有的条件,在仿射组合中没有,这一条件就保证了 0 ≤ θ ≤ 1 0\le\theta \le1 0≤θ≤1】
凸包
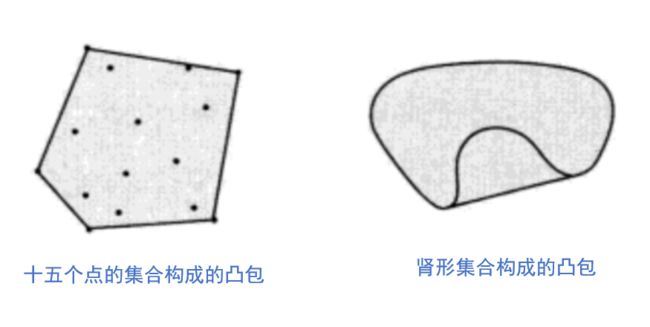
我们称集合C中所有点的凸组合的集合为凸包,记为 c o n v C convC convC。凸包总是凸的,它包含了C的最小的凸集。如果B是包含C的凸集,那么 c o n v C ⊆ B convC \subseteq B convC⊆B 。这里给出一些凸包的例子供大家理解【注意凸集的凸包就是其本身】
锥和凸锥
如果对于任意的 x ∈ C x \in C x∈C 和 θ ≥ 0 \theta \ge 0 θ≥0 都有 θ x ∈ C \theta x \in C θx∈C ,我们称集合C是锥。【可以看出齐次方程组 A X = 0 AX=0 AX=0 的解为锥】
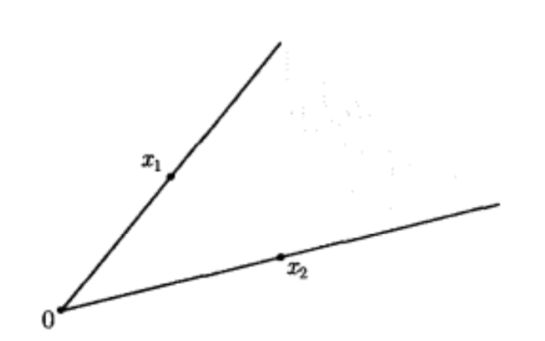
如果集合C是锥,并且C的凸的,则称C为凸锥,即对任意的 x 1 , x 2 ∈ C x_1,x_2 \in C x1,x2∈C 和 θ 1 , θ 2 ≥ 0 \theta_1,\theta_2 \ge 0 θ1,θ2≥0 ,都有 θ 1 x 1 + θ 2 x 2 ∈ C \theta_1x_1+\theta_2x_2 \in C θ1x1+θ2x2∈C 。从几何上来看,凸锥构成了一个扇形,扇形以0为顶点,两边分别通过 x 1 x_1 x1和 x 2 x_2 x2 ,如下图所示:
锥组合
具有 θ 1 x 1 + ⋯ + θ k x k , θ i ≥ 0 , i = 1 , ⋯ , k \theta_1x_1 + \cdots +\theta_kx_k ,\theta _i \ge 0 ,i=1, \cdots ,k θ1x1+⋯+θkxk,θi≥0,i=1,⋯,k 形式的点称为 x 1 , ⋯ , x k x_1 , \cdots ,x_k x1,⋯,xk 的一个锥组合。如果 x i x_i xi均属于凸锥C,那么 x i x_i xi 的每一个锥组合也在C中,也即集合C是凸锥的充要条件是它包含其元素的所有锥组合。
锥包
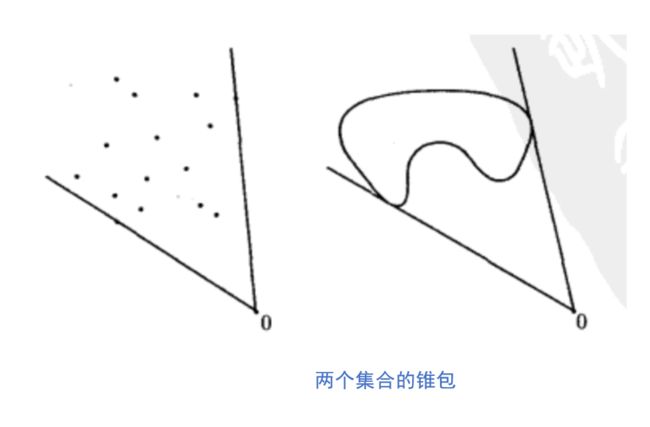
集合C的锥包是C中元素的所有锥组合的集合,锥包是包含C的最小的最小的凸锥。这里给出一些锥包的例子供大家理解
重要例子
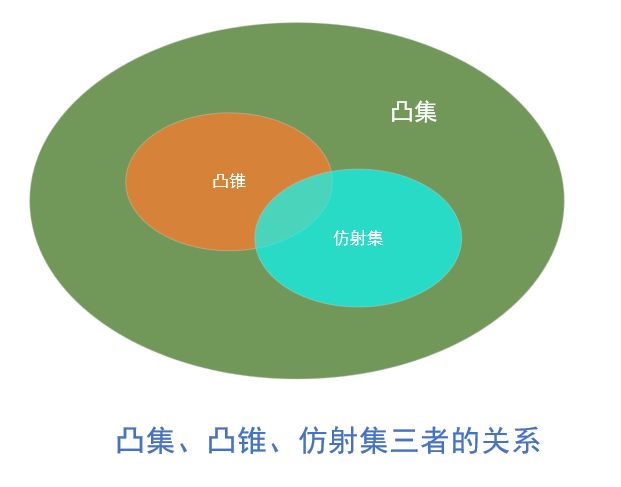
凸集、凸锥、仿射集三者关系图
如若文章对你有所帮助,那就
咻咻咻咻~~duang~~点个赞呗