李宏毅老师2020机器学习(深度学习)——知识点总结篇(1-20)
李宏毅老师2020机器学习——知识点总结篇(1-20)
李宏毅老师2020机器学习课程主页:
http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html
视频链接地址:
https://www.bilibili.com/video/BV11E41137sE?p=1
目录
-
- 李宏毅老师2020机器学习——知识点总结篇(1-20)
- 1 Machine Learning
- 2 Rule of ML
- 3 Regression Case Study
-
- 3.1 convex 凸函数
- 3.2 Regularization 正则化
- 4 Where does the error come from?
-
- 4.1 Variance&Bias
- 4.2 Underfitting&Overfitting
- 5 HW1 Regression
- 6 Gradient Descent-1
-
- 6.1 Learning Rate
-
- 6.1.1 Adagrad
- 6.1.2 Stochastic Gradient Descent
- 6.1.3 Feature Scaling
- 6.2 Gradient Descent
- 6.3 Limitation of Gradient Descent
- 7 Gradient Descent-2
- 8 Gradient Descent-3
- 9 Classfication
- 10 Logistic Regression
- 11 HW2 Classification
- 12 Introduction of Deep Learning
- 13 Backpropagation
- 14 Tips of Deep Learning
-
- Training
-
- Learning Rate
- Local minima
- Testing
-
- Early Stopping
- Regularization
- Dropout
- 15 Why deep
- 16 Convolutional Neural Network
- 17 HW3
- 18 Recurrent Neural Network(P1)
- 19 Recurrent Neural Network(P2)
- 20 Semi-supervised Learning
-
- 20.1 Semi-supervised Learning for Generative Model
- 20.2 Low-density Separation Assumption
- 20.3 Smoothness Assumption
注:本知识点仅供大家参考和快速了解这门课,每一节均为笔者听后仅总结细节和重点(而无基础知识),李宏毅老师的课程非常好,详细学习的读者还是请自行一一观看学习。作业代码也在持续整理。
以下顺序均参照视频顺序,无缺无改
1 Machine Learning
课程梗概,ML就是找函式
2 Rule of ML
课程要求,不再阐述
3 Regression Case Study
3.1 convex 凸函数
使用梯度下降的线性回归LR是没有Local optimal局部最优点(鞍点)的问题,因为LR的损失函数是convex的(凸函数),类似于等高线的损失函数,非凸函数是存在local optimal问题的,LR的损失函数如下:
l o s s ( Y ^ , Y ) = − ( y log Y ^ + ( 1 − y ) log 1 − Y ^ ) loss(\hat{Y},Y) = - (y\log{\hat{Y}} + (1-y)\log{1-\hat{Y}}) loss(Y^,Y)=−(ylogY^+(1−y)log1−Y^)
通俗而言,无论起点是哪里,不同方向最终找到的最优点都是一样的,像是一幅等高线图中往中间走就是最优
3.2 Regularization 正则化
原本的loss:
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 L=\sum_n({\hat{y}^n - (b+\sum{w_ix_i})})^2 L=n∑(y^n−(b+∑wixi))2
引入正则化:
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 + λ ∑ ( w i ) 2 L=\sum_n({\hat{y}^n - (b+\sum{w_ix_i})})^2 + \lambda\sum{(w_i)^2} L=n∑(y^n−(b+∑wixi))2+λ∑(wi)2
加入这项后会使得参数w越小越好,那我们为什么希望参数越小越好?因为这样在输入数据(测试数据)有较大变化时,预测的结果也不会有很大的变化,更平滑,将更不会被噪音干扰。但是正则项太大的话,模型将非常平滑,效果也会变差,所以这是个需要调的参数
4 Where does the error come from?
4.1 Variance&Bias
老师讲了一个很直观的例子,我们的误差来自哪里?来自于Variance&Bias:
假如目标是靶心,瞄准的位置与靶心的距离是Bias,瞄准的位置与实际击中的距离是Variance
靶心: f ^ \hat{f} f^
实际击中位置: f ⋆ f^\star f⋆,训练出的模型
瞄准位置: f ‾ \overline{f} f= E [ f ⋆ ] E[f^\star] E[f⋆] 期望值 = Bias
基于此,复杂模型将会有更大的Variance(分布更广)、更小的Bias(距靶心更近)
通俗而言,简单模型的范围更小,复杂模型的范围更广。此时每次在范围中取样算损失时,简单模型可能会只有一个点距离目标最近,因此简单模型预测结果聚堆;复杂模型可能会有多个区域距离目标更近,因此复杂模型预测结果更分散
4.2 Underfitting&Overfitting
Bias大:Underfitting——redesign model重新设计模型,增加复杂度
Variance大:Overfitting——More data增加数据 + Regularization正则化
数据增强方法:
- 图像——旋转 + 左右颠倒
- 文本——EDA
- 语音——加噪音、变声器、Google发音
5 HW1 Regression
作业回归预测,手写梯度下降,已写完,全部写完会整体更新上来代码文件。
6 Gradient Descent-1
6.1 Learning Rate
6.1.1 Adagrad
考虑让learning rate随epochs越来越小,如 μ t = μ / t + 1 \mu_t = \mu/\sqrt{t+1} μt=μ/t+1
比如在Adagrad中的 μ t σ t \frac{\mu_{t}}{\sigma_t} σtμt,其中 σ t \sigma_t σt是过去所有该参数梯度的平方求和后平均并开方,即
σ t = 1 t + 1 ∑ i = 0 t ( g i ) 2 \sigma_t = \sqrt{\frac{1}{t+1}\sum_{i=0}^t(g_i)^2} σt=t+11i=0∑t(gi)2
其中 g i g_i gi为该参数已经求过的梯度值
由此在Adagrad中,我们将得到
w t + 1 = w t − μ ∑ i = 0 t ( g i ) 2 g t w_{t+1} = w_t - \frac{\mu}{\sqrt{\sum_{i=0}^t(g_i)^2}}g^t wt+1=wt−∑i=0t(gi)2μgt
且值得注意的是梯度越大的时候,分母反而越大,更新的越慢,故有这样的解释Adagrad是考虑到了二次微分,以分母代替二次微分
6.1.2 Stochastic Gradient Descent
SGD批量梯度下降,比看过所有数据后再算loss更快
6.1.3 Feature Scaling
数据规范化,使得梯度下降更新参数更有效
6.2 Gradient Descent
一个有趣的问题,我们每一步的loss都在持续下降么?
答案当然是否,其数学原理如下
可以根据泰勒展开代替当前的loss,最优化当前参数使得loss最小,数学表达式就是向量点积的最小值,最优化的结果和梯度下降的结果一样。这就是在学习率足够小的时候,才能保证我们的梯度下降的更新值是正好满足泰勒展开的loss的
6.3 Limitation of Gradient Descent
梯度下降存在这样一个问题,一般而言我们只能想到局部最优点问题,但其实还有本身梯度为0的点,梯度值很小的点,且这些点对应的loss还很大。
7 Gradient Descent-2
“帝国时代”模拟梯度下降的示范:),梯度下降是分不出局部最优点和最优点的
8 Gradient Descent-3
“我的世界”说明为什么用梯度下降方法反而会不降反升,哈哈哈哈哈爱了爱了
9 Classfication
根据已有点,“穷举”期望(均值)、相干矩阵使得Gaussian高斯分布的累乘概率值最大,这个期望(均值)和相干矩阵就是最有可能产生已有点的参数。
且对于不同类别共享相干矩阵可以减少模型参数会避免过拟合,极大提高测试集的准确率
数学推导sigmoid过程解释为什么要共用相干矩阵
10 Logistic Regression
逻辑回归和线性回归的对比,包含了函数式、评价函数(损失函数)、怎么最小化损失函数
以及直接找参数w、b的方法Discriminative(逻辑回归)和通过高斯分布假设找w、b的方法Generative的不同,同一组训练数据通过不同方法找出的参数也不同。以及Discriminative训练效果好于Generative的原因,但其实Discriminative的方法也并不是在所有情况下都更优,如数据集很小、数据集有噪音Generative更好
可以通过多组的LR实现Feature Transformation
11 HW2 Classification
作业2分类任务,两种实现方法:1 Generative根据均值和共现矩阵算概率 2 Discriminative 通过数据直接算w和b,已整理完。
12 Introduction of Deep Learning
Deep Learning简要历史,及解释
三个步骤:建立NN模型 + 评价模型好坏(损失函数)+ 怎么优化模型(梯度下降)
一个有趣的思考问题:其实“Fat” 只用一个隐藏层但是无数个神经元的Fat Network就可以表示所有的函数关系了,那为什么我们还要deep加层数,而不是在每层中加更多的神经元?
13 Backpropagation
BP就是实现梯度下降的高效演算法,只需记住链式法则即可。
14 Tips of Deep Learning
Training
模型在训练集上效果不好,换模型架构。可以考虑下面两种方法:
Learning Rate
激活函数从Sigmoid到ReLU可以解决梯度消失的问题,及进阶版激活函数Leakly ReLU、Parametric ReLU和 Maxout,ReLU其实就是一种特殊的Maxout。且值得一提的是Maxout也是“可学习的”。以及Adagrad、RMSProp
Local minima
局部最优点问题,其实在神经网络中不需要考虑这个问题,除非这个局部最优点在每个维度都是局部最优点。但还有这样的一种解决方式,Momentum惯性,根据前一个时间点的梯度和现在的梯度作为方向。
Adam = RMSProp + Momentum
Testing
在测试集上效果不好,可以考虑如下三个方法:
Early Stopping
传统方法:早停法。在测试集loss不再下降的地方停止,这样测试集的效果最好。但是我们是不知道测试集的loss的,故用验证集来代替,在验证集效果最好的地方早停。
Regularization
传统方法:正则项。重新定义损失函数,如L1正则项等于在损失函数后再加参数w的绝对值的和,L2正则项在损失函数后再加w参数平方的和。这样在每次更新w的时候w就越来越靠近0。这种每次使得参数w小一点小一点的方式就叫做Weight Decay。
L2正则项:
L o s s ′ = L o s s + λ 1 2 L 2 , L 2 = ( w 1 ) 2 + ( w 2 ) 2 + . . . Loss' = Loss + \lambda \frac{1}{2}L_2,L_2 = (w_1)^2 + (w_2)^2 +... Loss′=Loss+λ21L2,L2=(w1)2+(w2)2+...
L1正则项:(绝对值不可微?在不可微点0可以直接给定值)
L o s s ′ = L o s s + λ 1 2 L 1 , L 1 = ∣ w 1 ∣ + ∣ w 2 ∣ + . . . Loss' = Loss + \lambda \frac{1}{2}L_1,L_1 = |w_1| + |w_2|+... Loss′=Loss+λ21L1,L1=∣w1∣+∣w2∣+...
通俗点说,每次更新参数,L1是减固定值,L2是乘上一个小数(0<小数<1,如0.99);这样对于较大的参数w因为有L2存在每次更新都能变得更小,较小参数w因L1每次减定值也能更新地更小。
Dropout
在训练时每次都随机选择隐藏丢掉一样神经元,在测试时无dropout,且假如训练时dropout比例是p%则测试时要对参数均乘上1-p%。Dropout是一种终极ensemble。
15 Why deep
正如12所问,为什么不要Fat,却选择要Deep的网络。
假设我们的Deep和Shallow(Fat)网络参数一样多,此时是矮胖的Shallow比较强还是高瘦的Deep比较强呢?答案不言而喻,且Deep是远远好于Fat的。那为什么会这样?
Deep -> Modularization模组化 + More Analogy + End-to-end Learning
Layers form basic to complex
16 Convolutional Neural Network
CNN其实就是DNN的简化版
C N N = ( C o n v o l u t i o n + M a x P o o l i n g ) n + F l a t t e n + F u l l y C o n n e c t e d F e e d f o r w a r d n e t w o r k CNN = (Convolution + Max Pooling)_n + Flatten + Fully Connected Feedforward network CNN=(Convolution+MaxPooling)n+Flatten+FullyConnectedFeedforwardnetwork
注:MaxPooling也是可以微分的
该怎么看CNN中Convolution的每个filter都关注了什么?固定模型参数,调整输入x使得该filter的参数矩阵的之和最大,此时的x就代表了每个filter的关注点。在flatten前每个filter关注的是图中的纹路,flatten后每个filter关注的就是整张图
Deep Style思想:
将要被转换风格的图片丢给CNN得到filter的输出当作这张图的Content
接下来把如呐喊这张图片也丢到CNN里面也得到filter的输出,但此时我们并不考虑这个输出值是多少,而是在意filter间的相关性,这个相关性也就代表了呐喊这张图的Style
最后,找一张图片输入给CNN使得它的filter输出像Content,同时filter间的相关性像Style,那么这张图片就是转换风格后的图片
17 HW3
作业3,通过CNN分类食物图片,共11类。torch版已整理完
18 Recurrent Neural Network(P1)
将hidden laryer存起来,在下个时间点再读进来这个叫Elman Network;另外一种存整个时间点的输出,在下个时间点再读进来这个就叫Jordan Network
Bidirectional RNN相当于考虑了整个sequence,比单向RNN只看句子的前半部分得到更好的效果
LSTM:Input Gate + Forget Gate + Output Gate,这三个门都是自己学出来的

不了解LSTM的读者推荐去看原片中28:19的”人体LSTM例子“
19 Recurrent Neural Network(P2)
RNN是用梯度下降训练的,演算法就是BPTT
然而RNN的训练是比较困难的,用梯度下降更新参数时很有可能出现下面的情况。

为什么要把RNN换成LSTM,因为LSTM可以解决gradient vanishing梯度消失;在LSTM中的Memory是可以被forget gate洗掉
GRU就是Input gate和Forget gate联动版
20 Semi-supervised Learning
Semi-supervised: labeled + unlabeled
Transductive learning: ublabeled data = test data feature
Inductive learning: ublabeled data != test data feature
20.1 Semi-supervised Learning for Generative Model


第一个目标函数是有标签的概率函数,第二个便是带有无标签数据的概率函数
20.2 Low-density Separation Assumption

这种Self-training方法与Generative的方法区别在于Self-training用的是Hard label而非Soft label。对于神经网络而言,Hard label会有效。
还有一种进阶版方法,如下图,通过计算unlabel data的cross entropy来定义这个unlabel data预测得到的标签好不好。并将这个E加到损失函数中,这种方法很像正则项。

还有一种不错的Semi方法

这种Semi-supervised SVM的原理就是穷举所有的unlabel data,并通过svm划分类,期望找到一种boundary能使margin最大,但error最小。当然在实作中并不会真正的穷举,仅是通过小样本改变来判断,具体细节请参见上图论文
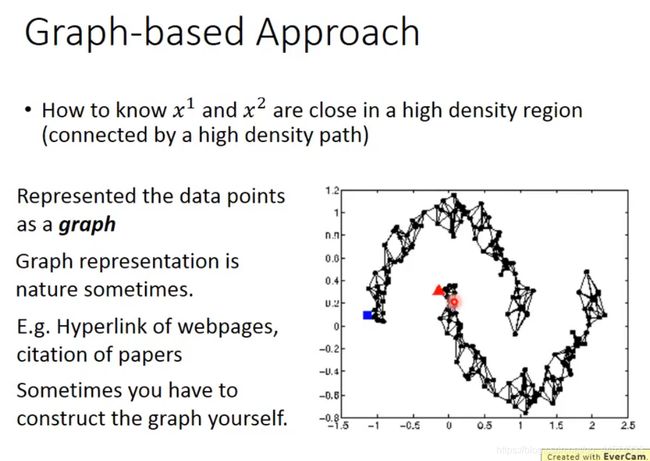
20.3 Smoothness Assumption
有这样一种假设,如果x1、x2在高密度空间相似,那么它们的y也就相似。
实作上,最简单的实现方法就是Cluster and then Label,更好的Cluster方法是deep auto-encoder 抽feature然后再做cluster。