图形学基础知识：重心坐标（Barycentric Coordinates）

前言

在前面的文章中我们经常提到知道某个三角形三个顶点的属性，然后就可以求出三角形内部某一点对应的属性。例如深度缓存的时候，高洛德着色的时候等等，但是我们一直没有说具体应该如何计算，本文就来介绍一下这一部分内容。

想要计算三角形内部某一点对应的属性，也就是我们一直说的三角形的插值，就需要用到重心坐标的概念。

 

直线的重心坐标

在讲三角形的重心坐标前，我们先来看一看直线上的重心坐标是怎么定义的。

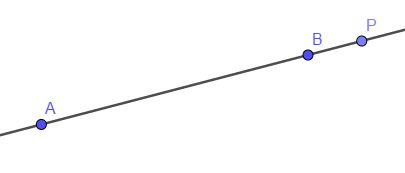
求直线上任意一点

设我们有两个点 A  和 B  ，它们可以连成一条直线。那么该直线上的任意一点 P  必然满足：

k为一个常数，其值也很好求，取任意轴三个点值进行计算即可：

然后我们可得：

 

因为 即 。

而  通过向量的减法，我们可以理解为 ，同样的 ，那么就可得到  ，然后可以得到 ，最终简化可得：

而  ，， 分别代表的就是 P，A，B三个点的坐标，因此可得

P = (1 - k)A + kB

因为 P = ((1-k)+k)P 因此上面式子可以变为 (1-k)A+kB-((1-k)+k)P=0，化简为 (1-k)(A-P)+k(B-P)，即：

 

几何意义

前面我们得到 ，即AP的长度  为 AB的长度  的k倍。而 BP的长度  又等于 ，因此  的长度为  的 1-k 倍。所以可得：

因为长度是没有正负的，然而实际上k可能为负数，就会导致上面的公式不对。我们先来看看下面三种情况：

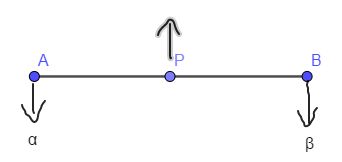
0 <= k <= 1

此时P在AB之间，如下图

可得

k < 0

k < 0 ，也就是说  方向和  相反，此时P在AB之外，离A更近一些，如下图

可得

k > 0

和前者相反，如下图

可得

总结

可以发现我们只要取绝对值，就可以满足上面的各种情况了，因此

 

直线上的重心坐标

通过上面的推导，我们就知道直线AB上的任意一点P，都可以由一个k来计算出来的。当然了，也可以通过P来推出k的值，怎么求上面已经说明过了。

若我们设 j = 1 - k，那么

P = jA + kB

j + k = 1

这样的话我们P就可以使用 (j, k) 的方式来表示，这种表示方式就是我们的重心坐标。同时需要注意，因为重心坐标是根据某一条直线的AB两点所定义的，因此不同的直线各自会有各自的重心坐标。

 

为什么叫重心坐标

在生活中想必大家都看过或挑过担子吧，人们在担子两边挂上重物，然后用肩膀扛起担子。如果担子两边的物体差不多重，我们要保持担子的平衡只需要把肩膀撑在担子的中间即可。但如果担子有一头特别的重，我们需要把肩膀尽可能的往重的那头靠近，才能保持住担子的平衡。

我们假设有线段AB（也就是担子），在A下面挂了质量为  的物体，在B下面挂了质量为  的物体,如下图：

若  ，那么重心P（肩膀的支撑点）应该在哪?自然线段的中心点了，如下图：

若  呢 ，那么P点的位置又应该在哪呢？通过常识我们应该知道，此时P点位置离A点更近一些，如下图：

那么如果 > 0， = 0 呢？那不就变得担子一边没有重物，我们只需要扛有重物的那一边了，即P在A点上，如下图：

既然可以等于0了，那么能不能等于负数呢？即  > 0， < 0，P会在哪呢？之前说  和  代表的质量，那么我们怎么理解负数的质量呢，我们知道挑担子的时候质量会造成向下的重力，那么负数的质量我们可以理解成在B点有一个向上的力，等于有人在担子的一边帮你搭把手，那就变成不是挑担子了，而是两个人抬东西了。两个人要用棍子抬一个东西，那么东西自然是在两个人中间了，因此P会在A的左边，如下图：

 或  某个值小于0的情况，也就把我们的P的位置从线段AB拓展到直线AB上了。当然了，我们不能 < 0， < 0，这样担子就飞起来了。

上面的例子说明了只要确定了  和  的值，也就确定了 重心P 的位置，怎么样是不是和前面所说的很像？事实上，只要保证 ， 我们的  就是前面所说的 j 的值，而  就是 k 的值，所以称这样的坐标为重心坐标。

 

三角形上的重心坐标

定义

与直线上任意一点满足 P = jA + kB 一样，在三角形ABC所在平面上的任意一点P同样满足

P = iA + jB + kC

i + j + k = 1

那么P用 (i, j, k) 的方式表示，就是在三角形上的重心坐标。同样的，因为重心坐标是由三角形的三个顶点所定义的，因此不同的三角形有各自的重心坐标。

同样的，若点P要在三角形内部或边上，需要满足 i >= 0，j >= 0，k >= 0，否则点P在三角形所在平面外。

同样由于 P = (i+j+k)P = iP+jP+kP，因此我们可得到 iA+jB+kC-iP-jP-kP = 0 即：

和直线比喻成担子类似，对于三角形也是一样的，我们可以假设有个三角形，它本身是没有质量的，但是我们在它的三个顶点位置分别悬挂了不同质量的物体，如果我们能找到其中一个点，能够使三角形保持平衡，那么这个点就是三角形的重心，如下图。

 

三角形和直线的关系

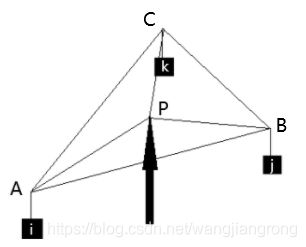
我们将三角形ABC的某个顶点（例如C）和三角形内任意一点P连线，并衍生到三角形的某条边上，设交点为D，如下图：

那么D点在AB上的位置，我们不就可以用直线的重心坐标表示么，我们设：D = xA + yB，其中 x + y = 1

知道D点坐标后，那么P点在CD的坐标我们又可以用直线的重心坐标表示，我们设：P = wC + zD，其中 w + z = 1

把D带入得：P = wC + z(xA + yB) = zxA + zyB + wC，而 zx + zy + w = z(x + y) + w = z + w = 1

那么设 i = zx，j = zy，k = w，不就证明了 P = iA + jB + kC 成立。

 

解i，j，k的值

接下来，我们来看看i，j，k三个值怎么计算，因为 i+j+k=1，因此k=1-i-j，也就是只要求两个未知数i和j即可。那么我们只需要找到两个方程组，解二元一次方程式即可。

因为 P = iA + jB + kC 因此 ，从中我们就可以取得两个方程式：

注：取x，y的话，也方便在二维空间中理解，当然也可以去x，z或y，z去计算。

解得

去 i ，得

此时方程式中只有一个 j 是变量，我们继续解，得

解得

解得

去分母，解得

即可求得 j 的值：

同理可解的 i 的值：

至于k的值，1-i-j 即可。

 

几何意义

我们将点P和三个顶点分别连线，可以得到三个新的三角形，如下图：

我们设三角形的总面积为 s，三角形PBC的面积为 a，三角形PAB的面积为 c，三角形PCA的面积为 b，那么可得：

也就是说重心坐标和每个顶点所相对的三角形（例如A对应的是PBC）的面积比有关。

我们来简单的推导一下：

前面我们知道

而  的值，不就是  的x值么，我们标记为 ，其他项也同理，那么我们可以得到

不知道大家对上面的这种  式子熟不熟悉，它正是二维向量叉乘的模（不熟悉的可以看下叉乘相关知识）。因此我们可以得到

设夹角CBP为 α ，那么分子  ，同理分母就是三角形ABC的面积，因此  成立，其他也同理。

 

三角形的重心

我们知道三角形的重心点为三条中线的交点，如下图：

中线即是将三角形分成面积相等的两部分，例如 。

我们来看下O点的重心坐标是多少，根据前面，我们知道我们可以通过三个三角形 AOB，AOC，BOC的面积比来求得重心坐标。那么我们就来看看这三个三角形的面积比。

首先因为  而他们的高相等，因此 BD = DC，可得 ，那么  。同理我们可得

因此三角形的重心坐标即为  。同样的，关于重心O点的坐标我们可以通过下面公式计算：

 

实际应用场景

前面哔哔赖赖了一大堆，我们知道可以通过重心坐标来计算三角形内某点的坐标，即

P = iA + jB + kC

ABCP代表的都是位置信息，我们可以通过位置信息求出重心坐标。而重心坐标牛逼就牛逼在，我们可以把ABCD的信息用别的任何信息来代替，例如颜色，法线，uv，深度等，然后套用上面的公式即可求出P点对应的属性。

例如我们A点红色(1,0,0)，B点绿色(0,1,0)，C点蓝色(0,0,1)，那么三角形内任何点的颜色就等于它的重心坐标，例如重心点颜色为 。

我们可以简单的用Unity写个demo验证一下

首先用下面脚本绘制一个三角形，三角形内部的颜色Unity已经为我们插值好了

[ExecuteInEditMode]
public class Triangle : Graphic
{
    Vector2 positionA = new Vector2(70, 40);
    Vector2 positionB = new Vector2(100, 100);
    Vector2 positionC = new Vector2(40, 70);
    
    protected override void OnPopulateMesh(VertexHelper vh)
    {
        vh.Clear();
 
        vh.AddVert(positionA, Color.red, Vector2.zero);
        vh.AddVert(positionB, Color.green, Vector2.zero);
        vh.AddVert(positionC, Color.blue, Vector2.zero);
        vh.AddTriangle(0, 1, 2);
    }
}

效果如下（注意color space要使用gamma的）：

然后怎么验证呢，我们可以创个小Image，然后通过它的坐标和三个顶点的坐标，我们就可以计算出小Image所在点对应的重心坐标，知道重心坐标和三个顶点颜色后，就可以计算出对应颜色，赋值给小Image，然后对比下颜色即可。代码如下：

using UnityEngine;
using UnityEngine.UI;

public class NewBehaviourScript : MonoBehaviour
{
    public Image self;
    
    Vector2 a = new Vector2(70, 40);//red
    Vector2 b = new Vector2(100, 100);//green
    Vector2 c = new Vector2(40, 70);//blue
    
    void Update()
    {
        Vector2 p = transform.position;

        float i = (-(p.x - b.x) * (c.y - b.y) + (p.y - b.y)*(c.x - b.x)) /
                  (-(a.x - b.x)*(c.y - b.y) + (a.y - b.y)*(c.x - b.x));
        float j = (-(p.x - c.x) * (a.y - c.y) + (p.y - c.y)*(a.x - c.x)) /
                  (-(b.x - c.x)*(a.y - c.y) + (b.y - c.y)*(a.x - c.x));
        float k = 1 - i - j;
        Debug.Log($"({i}, {j}, {k})");

        self.color = new Color(i, j, k);
    }
}

效果如下：

可以看出在三角形内部时，我们计算得到的颜色和Unity做好的插值是一样的。

至于除了颜色外的其他属性插值，原理也都是一样的，只要了解重心坐标了即可。也就是说我们只需要先通过四个点的位置信息算出重心坐标，然后就可以通过重心坐标来计算其他属性的插值。

 

重心坐标与投影

前面一套套下来，我们可能会有个疑惑，重心坐标的计算和z轴没有关系么？

注：其实更准确的说法是只和x，y，z中其中任意两项有关，具体可以看求i，j，k时，我们取的二元一次方程式是哪两个轴，当然通常情况下，就是取的x和y。

不考虑z，等于把空间中的三角形去掉z，即投影到平面xy上，即原本的A点 ，B点 ，C点  变成了A'点 ，B'点 ，C'点 。原本空间中三角形内的P点 ，同样投影变成了 P' 点  。那么投影前后，P和P' 的重心坐标一样么？答案是一样的！

公式没考虑z其实就已经告诉我们答案了，那么几何上，我们怎么理解呢，我们可以看个最简单的例子，就是重心。

我们假设下图中的三角形是空间中的三角形，也就是ABC的z轴值不同，重心点O的重心坐标自然是

那么我们看看投影后还是不是就可以了。

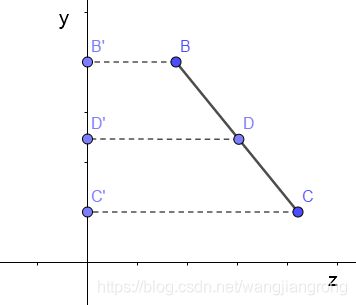
很简单，我们先来看边BC的投影，如下图，我们在yz平面看边BC的投影

可以发现投影后 D' 依旧是 B' 和 C' 的中心点（相似三角形原理），也就是说投影后的直线 A'D' 是三角形 A'B'C'的中线。其他中线同理，因此投影后 O' 的还是三角形A'B'C'的重心，其重心坐标还是。

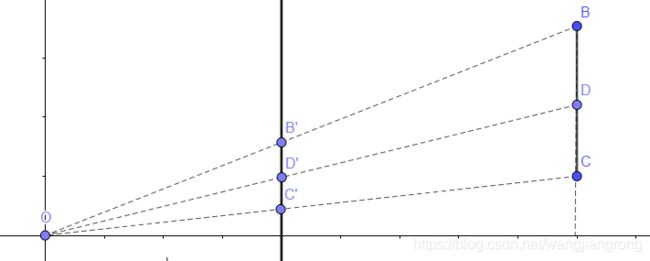
但是！有一种投影不行，就是透视投影，依旧是上面的三角形的边BC，我们来看看透视投影会发生什么，如下图：

很明显我们就可以看出来，此时 D' 不再是 B' 和 C' 的中心点。当然了，数学不能光用眼睛看，我们需要推导

为了方便计算，我们设O点为原点，O到投影屏幕的距离为 l （如上图所示），根据相似三角形可以得到：，即：。同理可得 ，

由于D是BC的中心点，根据直线的重心坐标我们可以知道  ，，带入可得：，而投影后B'C'的中点的y值应该是 ，可以发现和  并不相等。但是有个前提，那就是 ，否则 ，上面的式子依旧相等。用图来看的话更直观，如下图（依旧是相似三角形）：

emmm，好像直接看点D的重心坐标是否改变比看重心的更方便。

而且三角形重心坐标的这个变化同样适用于直线的重心坐标，事实上我们的举例就等于在看直线的重心坐标变化。

因此可以得出结论，在空间中的三角形或直线内的某个点，在投影变换前后，其的重心坐标可能会发生改变。因此有些计算，例如深度，一定要在投影变换前做，否则得到的结果可能是不对的。

 

矫正

但是前面那样太麻烦了，我们可不可以直接在知道变换前的重心坐标推出变换后的重心坐标，或者反过来呢？当然可以。

我们先从直线的重心坐标投影矫正开始，直接使用之前的图，如下：

此时D不再是BC的中心点了，而是当做BC中的任意一点。根据直线的重心坐标我们可以设： D = iB+(1-i)C，D的重心坐标即为(i, 1-i)。直线BC通过透视投影后得到直线B'C'，点D变为D'，我们知道透视投影后，重心坐标的值会变，所以我们设：D' = jB'+(1-j)C'，D'的重心坐标即为(j, 1-j)。

那么我们只需要知道 i 和 j 的相对关系，不就可以在只知道 i 或 j 中一个的情况下推出另个的值了么？例如，我们假设 i = 2j，那么投影前的重心坐标 (0.6, 0.4)在投影后自然变成的了(0.3, 0.7)，或者说投影后的重心坐标为(0.1, 0.9)，那么投影前就是(0.2, 0.8)。这样即使碰见投影变换，我们也可以通过变换后的重心坐标去推导出原本的重心坐标，不用再通过逆变换去求原本的重心坐标了。

当然前面 i = 2j 是我们瞎鸡儿说的，我们来看看真正的值是多少。

根据直线的重心坐标，我们可以很容易求得 j 的值：  （其实 i 的值同样可以直接算出来，然后和 j 一除就知道了，但是我们这边要推导出一个更简单的公式）。

通过相似三角形可以得到： ，，，带入 j 中可得： 。

我们先来看分子项，即 ，我们知道  ，，带入分子中，得到：

化简可得：

其中的  不就是分母中的那部分嘛，即可抵消掉，j 就可以简化为：

从这个式子也可以看出，z值相同时，则 i = j，重心坐标不变。也说明了之前一大串的  的值其实就是 i 。

做了个简单的验证，如下图，D点的重心坐标确实正好从 (1/3, 2/3) 变成了 (1/6, 5/6)。

---

接下来我们来讲讲三角形的重心坐标投影矫正

前面我们得到  ，那么三角形内任意一点P，我们可以看作是AD上的任意一点，我们设 P = wA+(1-w)D，投影后w会变为z，套用上面的公式，我们可以得到

因为P = wA+(1-w)D，D = iB+(1-i)C，所以 P = wA+(1-w)(iB+(1-i)C)，即：

P = wA+(i-iw)B+(1-i-w+iw)C

也就是P的重心坐标为(w, i-iw, 1-i-w+iw) 后面两项看着很复杂，我们先不管，写成 (w, ?, ?)，那么我们就知道投影后重心坐标会变为  。

那后面两个怎么算呢？既然我们可以把D看成是BC上的一点，P是AD上的点，那么是不是可以再把D看成AB或AC上一点，P则是CD或BD上一点来推导上面的公式。

这样我们又会得到   和 

因此得出结论，假设在透视投影前，P在三角形ABC的重心坐标为(i, j, k)，那么投影后该坐标会变为 ，而  。