- 自然数是否包含0
二分掌柜的
数学物理自然数
自然数是否包含0flyfish自然数是否包含0,本质是数学定义随学科需求演变的结果,数论继承了“从1计数”的历史传统,而集合论与逻辑为追求公理化完备性将0纳入。视角自然数包含0吗?核心理由数论/计数否(从1开始)符合“物体个数”的直观意义,避免0在素数分解、数论函数中引发逻辑例外。集合论/逻辑是(从0开始)空集基数对应0,通过集合后继构造自然数,满足公理化体系的完备性。数论与早期教材:自然数从1开
- 【网络安全】网络安全中的离散数学
flyair_China
安全架构
一、离散数学核心知识点与网络安全映射1.数论(NumberTheory)知识点安全应用场景实例说明质因数分解RSA公钥加密大整数分解难题(2048位密钥需数万年破解)模运算Diffie-Hellman密钥交换利用(gamodp)实现安全协商欧拉定理RSA加密/解密me*d≡m(modn)保障解密还原中国剩余定理高效解密优化RSA-CRT加速解密运算达70%2.代数结构(AlgebraicStruc
- 数学中的代数数论与代数几何
AI天才研究院
计算AI大模型应用入门实战与进阶大数据人工智能语言模型AILLMJavaPython架构设计AgentRPA计算AI大模型应用
1.背景介绍在数学的众多分支中,代数数论和代数几何是两个极其重要的领域。代数数论,顾名思义,是研究数论问题的代数方法,主要研究整数、有理数、代数数等的性质。而代数几何则是研究零点集的代数方法,主要研究多项式方程和代数方程组的解的几何性质。这两个领域虽然看似独立,但实际上有着深厚的内在联系,它们的交叉研究已经产生了许多深远的理论和应用。2.核心概念与联系2.1代数数论代数数论的核心概念是代数数,即满
- 三生原理m 值的五周期循环是人为设定还是数论内在要求?
葫三生
三生学派算法人工智能机器学习量子计算数学建模
AI辅助创作:三AI辅助创作:生原理中m值的五周期循环(取值范围{0,1,2,3,4})本质上是数论内在要求,其必要性源于素数分布的周期性约束与代数结构的不可突破性,但部分特性受限于当前数学框架的观测维度。具体辩证关系如下:✅一、数论内在性的核心证据模周期对称性约束当m突破5周期(如m=5)时,三生原理的素数生成公式p=3(2n+1)+2(2n+m+1)必然生成合数:例如n=0,m=
- 【Algo】常见组合类数列
CodeWithMe
C/C++c++c语言算法
文章目录常见组合类数列1常见递推/组合类数列1.1基础递推类数列1.2组合数学数列1.3数论/函数类数列1.4图论/路径问题相关数列1.5算法和结构设计常用数列2示例:有规律数列前10项对比表3参考建议常见组合类数列介绍一些常见具有明显数学规律或递推关系的常见组合类数列。1常见递推/组合类数列1.1基础递推类数列Fibonacci数列F(n)=F(n-1)+F(n-2),F(0)=0,F(1)=1
- 数论:互质数的个数
Zephyrtoria
数据结构与算法java算法数论
数论:互质数的个数互质数的个数www.acwing.com/problem/content/4971/a=p1a1p2a2...pmama=p_{1}^{a_1}p_{2}^{a_2}...p_{m}^{a_m}a=p1a1p2a2...pmamab=p1a1bp2a2b...pmamba^{b}=p_{1}^{a_1b}p_{2}^{a_2b}...p_{m}^{a_mb}ab=p1a1bp2a
- 素数5在三生原理和费马数公式中均起临界作用的原因?
葫三生
三生学派机器学习人工智能算法量子计算数学建模
AI辅助创作:问答一:在数学理论中,素数5的“临界作用”在《三生原理》与费马数公式中均具有深刻的数学内涵,这种共性源于其独特的数论性质、结构对称性及计算阈值意义。以下从三个维度展开分析:一、5在《三生原理》中的临界性:阴阳平衡与生成韵律的转折点《三生原理》作为融合《周易》哲学的数论体系,其核心是将“三生万物”动态生成思想转化为素数分布的参数化模型。5的临界性体现在:最小满足阴阳参数联动的奇素数《三
- 算法-数论
cx_2023
算法c++开发语言
C-小红的数组查询(二)_牛客周赛Round95思路:不难看出a数组是有循环的d=3,p=4时,a数组:1、0、3、2、1、0、3、2.......最小循环节为4,即最多4种不同的数d=4,p=6时,a数组:1、5、3、1、5、3.......最小循环节为3d=4,p=10时,a数组:1、5、9、3、7、1、5、9、3、7.......最小循环节为5可以得出,最小循环节T=p/gcd(d,p)an
- 质数表的构建
羊儿~
c算法数据结构c++
前言最近,有很多人问我如何既能保证时间复杂度低又能正确的打出质数表,那么今天,我就给各位读者带来了几种打出质数表的(打表)的方法。1.质数的介绍质数,又称素数,是指在大于1的自然数中,除了1和它本身外,不能被其他自然数整除的数。换句话说,质数只有两个正因数:1和它自己。例如,2、3、5、7、11等都是质数。2是最小的质数,也是唯一的偶质数,其他质数都是奇数。质数在数学中具有重要地位,尤其在数论领域
- 使用MATLAB输出给定范围内的所有质数
士兵突击许三多
matlab基础matlab
使用MATLAB输出给定范围内的所有质数后续我将给出一些运用案例在计算机科学与数学中,质数是指仅能被1和其本身整除的自然数,例如2、3、5、7、11等。质数在数论和密码学中有着重要的应用。今天,我们将介绍如何使用MATLAB来生成并输出所有质数。什么是质数?质数是大于1的自然数,且只能被1和它自己整除。例如:2、3、5、7、11、13等都是质数。4、6、8、9、10等不是质数,它们都有其他因子。目
- 巧用数论与动态规划破解包子凑数问题
EtherWanderer
数据结构与算法蓝桥杯职场和发展
题目描述小明想知道包子铺用给定的蒸笼规格能凑出多少种无法组成的包子数目。若无法组成的数目无限,输出INF。输入格式第一行为整数NNN(蒸笼种数)接下来NNN行每行一个整数AiA_iAi(每种蒸笼的包子数)输出格式无法凑出的数目个数,若无限则输出INF问题分析关键条件若所有AiA_iAi的最大公约数(GCD)不为1,则无法组成的数目无限。例如,当所有数均为偶数时,无法组成任何奇数。动态规划思路当GC
- 解析数论基础:第二十四章 (s)与L(s,x)的阶估计
AI天才研究院
AI大模型企业级应用开发实战计算计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
解析数论基础:第二十四章(s)与L(s,x)的阶估计作者:禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来数论是数学的一个分支,研究整数和它们的性质。在数论中,(s)函数和L(s,x)函数是两个重要的函数,它们在解析数论、数论分析以及许多数学物理领域都有着广泛的应用。特别是在素数分布、素数定理以及黎曼ζ函数的研究中,(s)函数和
- 探索 C++ 中的数论世界:从基础到实践
光の
java算法开发语言搜索算法
一、引言数论作为数学的核心分支,在计算机科学领域展现出强大的生命力。无论是密码学中的RSA加密算法,还是编程竞赛中的算法优化,数论都扮演着不可或缺的角色。C++凭借其高效的性能和底层控制能力,成为实现数论算法的理想选择。本文将带您走进C++数论的世界,从基础概念到实际应用,逐步揭开数论的神秘面纱。二、数论基础概念与C++实现2.1质数判定质数是大于1且只能被1和自身整除的整数。在C++中,我们可以
- USST新生训练赛3KLMN
Fighter_sky
题解C++acm
题解前言题解部分KPashmakandParmida'sproblem(1800)题目大意题解参考代码LPashmakandGraph(1900)题目大意题解参考代码MLuckyChains(1600)题目大意题解参考代码NManipulatingHistory(1600)题目大意题解参考代码前言KLMN是数据结构(线段树/树状数组)+dp+数论+结论唐题题解部分KPashmakandParmid
- 数论:数学王国的密码学
菜鸟破茧计划
密码学
在计算机科学的世界里,数论就像是一把神奇的钥匙,能够解开密码学、算法优化、随机数生成等诸多领域的谜题。作为C++算法小白,今天我就带大家一起走进数论的奇妙世界,探索其中的奥秘。什么是数论?数论是纯粹数学的分支之一,主要研究整数的性质。在计算机科学中,数论尤其在密码学、算法设计和计算机安全等领域有着广泛的应用。数论中的一些基本概念包括质数、最大公约数、模运算等。数论的基本概念与代码实现质数判定质数是
- 数论专题R1(线性筛专题)
JL24zyl
c++
目录A反素数加强版B约数积函数Ch(n)Dg(n)E神必的函数F球与盒子总结A反素数加强版时空限制1s,32MB问题描述如果一个大于等于1的正整数n,满足所有小于n且大于等于1的所有正整数的约数个数都小于n的约数个数,则n是一个反素数。请你计算不大于n的最大反素数。输入格式第一行输入数据组数T,每组数据输入1个正整数n。输出格式对每组数据,输出不大于n的最大反素数。数据范围1=1)的约数个数为(r
- 为什么哈希加密后破解怎么难?单向函数;密码学的数学原理:从理论到实践
小胡说技书
#数据安全技术哈希算法密码学算法单向函数数据安全安全信息安全
文章目录一、单向函数的数学基础1.1单向函数的数学定义1.2复杂度理论视角1.3数论在密码学中的应用二、哈希函数的数学原理与不可逆性2.1从信息论角度理解哈希不可逆性2.2碰撞抵抗的数学分析2.3单向压缩函数与雪崩效应三、非对称密码系统的数学基础3.1RSA算法的数学原理3.2椭圆曲线加密的几何解析四、密码学随机性与熵的数学原理4.1随机性与熵的量化4.2伪随机数生成器的数学模型4.3加盐哈希的数
- “即时取模”的快读 → 数论
hnjzsyjyj
信息学竞赛#算法数学基础#快读“即时取模”的快读快读
【“即时取模”的快读】●“即时取模”的快读是一种在输入大整数时直接进行取模运算的优化技术,常用于处理需要大数运算但最终结果需取模的场景(如数论题目)。其核心思想是在逐位读取数字时同步计算模值,避免存储完整的大数。intread(){//fastreadintx=0,f=1;charc=getchar();while(c'9'){//!isdigit(c)if(c=='-')f=-1;c=getch
- 【算法笔记】ACM数论基础模板
寂空_
算法笔记算法笔记c++
目录几个定理唯一分解定理鸽巢原理(抽屉原理)麦乐鸡定理哥德巴赫猜想容斥原理例题二进制枚举解dfs解裴蜀定理例题代码最大公约数、最小公倍数最大公约数最小公倍数质数试除法判断质数分解质因数筛质数朴素筛法(埃氏筛法)线性筛法(欧拉筛法)约数试除法求约数求约数个数一个数求约数个数求1~n所有数的约数个数O(nlogn)O(nlogn)O(nlogn)筛法O(n)O(n)O(n)筛法约数之和一个数求约数之和
- 扩展欧几里得算法简介及代码实现
hnjzsyjyj
信息学竞赛#算法数学基础扩展欧几里得算法裴蜀定理
【扩展欧几里得算法简介】●扩展欧几里得算法(ExtendedEuclideanAlgorithm)是欧几里得算法的扩展版本,不仅能计算两个整数的最大公约数(GCD),还能找到满足贝祖等式(Bézout'sIdentity)ax+by=gcd(a,b)的整数解x和y。它在数论、密码学等领域有重要应用,例如求解模的逆元、求解线性同余方程等。●扩展欧几里得算法求ax+by=gcd(a,b)特解的方法如下
- 《夜深人静写算法》数论篇 - (10) 扩展欧几里得定理
英雄哪里出来
《夜深人静写算法》数论篇算法初等数论扩展欧几里得定理
前言 通过扩展欧几里得定理,利用扩展欧几里得算法,可以求解线性同余方程。 那么什么是线性同余方程?什么是扩展欧几里得定理?什么是扩展欧几里得算法?接下来的几篇文章会来讲解一下这几个概念。一、扩展欧几里得定理1、定理概述 对于不都为零的整数aaa和b
- 【ICPC】The 2024 ICPC Kunming Invitational Contest E
浅慕Antonio
算法竞赛开发语言c++算法
RelearnthroughReview#数论#枚举#gcd题目描述Givenanintegersequencea1,a2,⋯ ,ana_1,a_2,\cdots,a_na1,a2,⋯,anoflengthnnnandanon-negativeintegerkkk,youcanperformthefollowingoperationatmostonce:Choosetwointegerslllan
- 初等数论 --- 同余、欧拉定理、费马小定理、求逆元
chstor
算法笔记
文章目录一、同余二、欧拉定理三、费马小定理四、扩展欧几里得算法4.1裴蜀定理五、一元线性同余方程六、逆元求逆元方法一、扩展欧几里得算法求逆元方法二、费马小定理加快速幂一、同余定义当两个整数a,b除以同一个正整数m,若得相同余数,则二整数同余。记为:a≡b(mod m)当两个整数a,b除以同一个正整数m,若得相同余数,则二整数同余。记为:a\equivb(\modm)当两个整数a,b除以同一个正整
- 初等数论 课堂笔记 第三章 -- 欧拉函数一节的若干练习
此账号已停更
初等数论数学数论
练习计算φ(60)\varphi\left(60\right)φ(60)。解 将606060写成标准分解式60=22×3×560={{2}^{2}}\times3\times560=22×3×5法一(计算过程中出现分式)φ(60)=60×(1−12)(1−13)(1−15)=60×12×23×45=16\varphi\left(60\right)=60\times\left(1-\frac{1}
- 【关于数学】感悟(附学习目录)
DataPlayerK
线性代数抽象代数概率论矩阵
一些感悟数学具有艺术美。从某种意义上来说,数学家和画家本质相同,他们都在“刻画”心目中的图景。小时候我总是在思考一个终极问题:数学是什么?我怀念那时我单纯而热烈的执着,此文章就长期记载我对数学的看法吧。2017-2020高中在读数学是不同精巧结构的集合。高中数学竞赛中,不等式/组合数学/数论中充斥着各种“限制下的精巧结构”,使得结构出现了各种各样奇妙的性质。2021-4-14大一在读数学不仅重在结
- NOIP2009提高组.Hankson的趣味题
Ayanami_Reii
算法c++笔记蓝桥杯
目录题目算法标签:数论,最大公约数,最小公倍数,约数思路代码题目200.Hankson的趣味题算法标签:数论,最大公约数,最小公倍数,约数思路因为[x,a0]=b1[x,a_0]=b_1[x,a0]=b1因此xxx一定是b1b_1b1约数,注意到,数据范围是2×1092\times10^92×109如果直接使用试除法计算约数时间复杂度是O(nn)O(n\sqrtn)O(nn)会超时,因此需要进行优
- 数论---求组合数
@松田
算法c++组合数数论
快速幂:数论-----快速幂-CSDN博客快速幂求逆元:数论----快速幂求逆元-CSDN博客筛质数:筛质数----CSDN博客求组合数I//10万组a,busingnamespacestd;constintN=2010,mod=1e9+7;intc[N][N];voidinit(){for(inti=0;i>n;while(n--){inta,b;cin>>a>>b;coutusingnames
- 线性筛法求素数(欧拉筛法)(求质数,O(n)时间复杂度)(外加求每个整数的最小质因子)(python)
不染_是非
算法pythonpython算法开发语言
前言:python中求质数的方法有好几种,这里就讲解时间复杂度最低的算法欧拉筛法,时间复杂度为O(n),这是数论中也是算法比赛中必须掌握的方法。本篇博客还会额外讲解求每个整数的最小质因子,什么是质因子?顾名思义,就是是质数的因子,求这个有什么用呢?下篇博客X的因子链(数论,python)(算术基本定理)(欧拉筛法)会给大家讲解一道例题,在例题中讲解它的用法。思路:线性筛法的整体思路是(代码里有详细
- 解析数论基础:问题的提出和进展
AI天才研究院
AI大模型企业级应用开发实战DeepSeekR1&大数据AI人工智能大模型计算计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
解析数论基础:问题的提出和进展作者:禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来数论,作为数学的一个分支,自古以来就与算法和密码学紧密相连。从古代的算术运算到现代的计算机科学,数论问题始终是算法设计和理论分析的重要基础。随着计算机技术的发展,数论在加密算法、网络安全、计算机图形学、算法优化等领域发挥着越来越重要的作用。1.2
- 了解倒数的概念,乘法逆元就很好理解——解析之【逆元的概念】【逆元的求解方法】
灰阳阳
算法算法裴蜀定理欧几里得算法最大公约数逆元
目录前言一、逆元的概念1、基本定义示例1:a=3,m=7a=3,m=7a=3,m=7示例2:a=2,m=5a=2,m=5a=2,m=52、乘法逆元有什么用3、相关性质二、求解逆元的方法1、费马小定理求乘法逆元定义费马小定理求逆元的方法总结模板题2、扩展欧几里得算法求逆元定义扩展欧几里得算法求逆元的方法总结模板题3、递推公式求逆元定义递推公式的推导示例总结前言首先,下面讨论的是数论相关内容。主要研究
- Java实现的基于模板的网页结构化信息精准抽取组件:HtmlExtractor
yangshangchuan
信息抽取HtmlExtractor精准抽取信息采集
HtmlExtractor是一个Java实现的基于模板的网页结构化信息精准抽取组件,本身并不包含爬虫功能,但可被爬虫或其他程序调用以便更精准地对网页结构化信息进行抽取。
HtmlExtractor是为大规模分布式环境设计的,采用主从架构,主节点负责维护抽取规则,从节点向主节点请求抽取规则,当抽取规则发生变化,主节点主动通知从节点,从而能实现抽取规则变化之后的实时动态生效。
如
- java编程思想 -- 多态
百合不是茶
java多态详解
一: 向上转型和向下转型
面向对象中的转型只会发生在有继承关系的子类和父类中(接口的实现也包括在这里)。父类:人 子类:男人向上转型: Person p = new Man() ; //向上转型不需要强制类型转化向下转型: Man man =
- [自动数据处理]稳扎稳打,逐步形成自有ADP系统体系
comsci
dp
对于国内的IT行业来讲,虽然我们已经有了"两弹一星",在局部领域形成了自己独有的技术特征,并初步摆脱了国外的控制...但是前面的路还很长....
首先是我们的自动数据处理系统还无法处理很多高级工程...中等规模的拓扑分析系统也没有完成,更加复杂的
- storm 自定义 日志文件
商人shang
stormclusterlogback
Storm中的日志级级别默认为INFO,并且,日志文件是根据worker号来进行区分的,这样,同一个log文件中的信息不一定是一个业务的,这样就会有以下两个需求出现:
1. 想要进行一些调试信息的输出
2. 调试信息或者业务日志信息想要输出到一些固定的文件中
不要怕,不要烦恼,其实Storm已经提供了这样的支持,可以通过自定义logback 下的 cluster.xml 来输
- Extjs3 SpringMVC使用 @RequestBody 标签问题记录
21jhf
springMVC使用 @RequestBody(required = false) UserVO userInfo
传递json对象数据,往往会出现http 415,400,500等错误,总结一下需要使用ajax提交json数据才行,ajax提交使用proxy,参数为jsonData,不能为params;另外,需要设置Content-type属性为json,代码如下:
(由于使用了父类aaa
- 一些排错方法
文强chu
方法
1、java.lang.IllegalStateException: Class invariant violation
at org.apache.log4j.LogManager.getLoggerRepository(LogManager.java:199)at org.apache.log4j.LogManager.getLogger(LogManager.java:228)
at o
- Swing中文件恢复我觉得很难
小桔子
swing
我那个草了!老大怎么回事,怎么做项目评估的?只会说相信你可以做的,试一下,有的是时间!
用java开发一个图文处理工具,类似word,任意位置插入、拖动、删除图片以及文本等。文本框、流程图等,数据保存数据库,其余可保存pdf格式。ok,姐姐千辛万苦,
- php 文件操作
aichenglong
PHP读取文件写入文件
1 写入文件
@$fp=fopen("$DOCUMENT_ROOT/order.txt", "ab");
if(!$fp){
echo "open file error" ;
exit;
}
$outputstring="date:"." \t tire:".$tire."
- MySQL的btree索引和hash索引的区别
AILIKES
数据结构mysql算法
Hash 索引结构的特殊性,其 检索效率非常高,索引的检索可以一次定位,不像B-Tree 索引需要从根节点到枝节点,最后才能访问到页节点这样多次的IO访问,所以 Hash 索引的查询效率要远高于 B-Tree 索引。
可能很多人又有疑问了,既然 Hash 索引的效率要比 B-Tree 高很多,为什么大家不都用 Hash 索引而还要使用 B-Tree 索引呢
- JAVA的抽象--- 接口 --实现
百合不是茶
抽象 接口 实现接口
//抽象 类 ,方法
//定义一个公共抽象的类 ,并在类中定义一个抽象的方法体
抽象的定义使用abstract
abstract class A 定义一个抽象类 例如:
//定义一个基类
public abstract class A{
//抽象类不能用来实例化,只能用来继承
//
- JS变量作用域实例
bijian1013
作用域
<script>
var scope='hello';
function a(){
console.log(scope); //undefined
var scope='world';
console.log(scope); //world
console.log(b);
- TDD实践(二)
bijian1013
javaTDD
实践题目:分解质因数
Step1:
单元测试:
package com.bijian.study.factor.test;
import java.util.Arrays;
import junit.framework.Assert;
import org.junit.Before;
import org.junit.Test;
import com.bijian.
- [MongoDB学习笔记一]MongoDB主从复制
bit1129
mongodb
MongoDB称为分布式数据库,主要原因是1.基于副本集的数据备份, 2.基于切片的数据扩容。副本集解决数据的读写性能问题,切片解决了MongoDB的数据扩容问题。
事实上,MongoDB提供了主从复制和副本复制两种备份方式,在MongoDB的主从复制和副本复制集群环境中,只有一台作为主服务器,另外一台或者多台服务器作为从服务器。 本文介绍MongoDB的主从复制模式,需要指明
- 【HBase五】Java API操作HBase
bit1129
hbase
import java.io.IOException;
import org.apache.hadoop.conf.Configuration;
import org.apache.hadoop.hbase.HBaseConfiguration;
import org.apache.hadoop.hbase.HColumnDescriptor;
import org.apache.ha
- python调用zabbix api接口实时展示数据
ronin47
zabbix api接口来进行展示。经过思考之后,计划获取如下内容: 1、 获得认证密钥 2、 获取zabbix所有的主机组 3、 获取单个组下的所有主机 4、 获取某个主机下的所有监控项
- jsp取得绝对路径
byalias
绝对路径
在JavaWeb开发中,常使用绝对路径的方式来引入JavaScript和CSS文件,这样可以避免因为目录变动导致引入文件找不到的情况,常用的做法如下:
一、使用${pageContext.request.contextPath}
代码” ${pageContext.request.contextPath}”的作用是取出部署的应用程序名,这样不管如何部署,所用路径都是正确的。
- Java定时任务调度:用ExecutorService取代Timer
bylijinnan
java
《Java并发编程实战》一书提到的用ExecutorService取代Java Timer有几个理由,我认为其中最重要的理由是:
如果TimerTask抛出未检查的异常,Timer将会产生无法预料的行为。Timer线程并不捕获异常,所以 TimerTask抛出的未检查的异常会终止timer线程。这种情况下,Timer也不会再重新恢复线程的执行了;它错误的认为整个Timer都被取消了。此时,已经被
- SQL 优化原则
chicony
sql
一、问题的提出
在应用系统开发初期,由于开发数据库数据比较少,对于查询SQL语句,复杂视图的的编写等体会不出SQL语句各种写法的性能优劣,但是如果将应用系统提交实际应用后,随着数据库中数据的增加,系统的响应速度就成为目前系统需要解决的最主要的问题之一。系统优化中一个很重要的方面就是SQL语句的优化。对于海量数据,劣质SQL语句和优质SQL语句之间的速度差别可以达到上百倍,可见对于一个系统
- java 线程弹球小游戏
CrazyMizzz
java游戏
最近java学到线程,于是做了一个线程弹球的小游戏,不过还没完善
这里是提纲
1.线程弹球游戏实现
1.实现界面需要使用哪些API类
JFrame
JPanel
JButton
FlowLayout
Graphics2D
Thread
Color
ActionListener
ActionEvent
MouseListener
Mouse
- hadoop jps出现process information unavailable提示解决办法
daizj
hadoopjps
hadoop jps出现process information unavailable提示解决办法
jps时出现如下信息:
3019 -- process information unavailable3053 -- process information unavailable2985 -- process information unavailable2917 --
- PHP图片水印缩放类实现
dcj3sjt126com
PHP
<?php
class Image{
private $path;
function __construct($path='./'){
$this->path=rtrim($path,'/').'/';
}
//水印函数,参数:背景图,水印图,位置,前缀,TMD透明度
public function water($b,$l,$pos
- IOS控件学习:UILabel常用属性与用法
dcj3sjt126com
iosUILabel
参考网站:
http://shijue.me/show_text/521c396a8ddf876566000007
http://www.tuicool.com/articles/zquENb
http://blog.csdn.net/a451493485/article/details/9454695
http://wiki.eoe.cn/page/iOS_pptl_artile_281
- 完全手动建立maven骨架
eksliang
javaeclipseWeb
建一个 JAVA 项目 :
mvn archetype:create
-DgroupId=com.demo
-DartifactId=App
[-Dversion=0.0.1-SNAPSHOT]
[-Dpackaging=jar]
建一个 web 项目 :
mvn archetype:create
-DgroupId=com.demo
-DartifactId=web-a
- 配置清单
gengzg
配置
1、修改grub启动的内核版本
vi /boot/grub/grub.conf
将default 0改为1
拷贝mt7601Usta.ko到/lib文件夹
拷贝RT2870STA.dat到 /etc/Wireless/RT2870STA/文件夹
拷贝wifiscan到bin文件夹,chmod 775 /bin/wifiscan
拷贝wifiget.sh到bin文件夹,chm
- Windows端口被占用处理方法
huqiji
windows
以下文章主要以80端口号为例,如果想知道其他的端口号也可以使用该方法..........................1、在windows下如何查看80端口占用情况?是被哪个进程占用?如何终止等. 这里主要是用到windows下的DOS工具,点击"开始"--"运行",输入&
- 开源ckplayer 网页播放器, 跨平台(html5, mobile),flv, f4v, mp4, rtmp协议. webm, ogg, m3u8 !
天梯梦
mobile
CKplayer,其全称为超酷flv播放器,它是一款用于网页上播放视频的软件,支持的格式有:http协议上的flv,f4v,mp4格式,同时支持rtmp视频流格 式播放,此播放器的特点在于用户可以自己定义播放器的风格,诸如播放/暂停按钮,静音按钮,全屏按钮都是以外部图片接口形式调用,用户根据自己的需要制作 出播放器风格所需要使用的各个按钮图片然后替换掉原始风格里相应的图片就可以制作出自己的风格了,
- 简单工厂设计模式
hm4123660
java工厂设计模式简单工厂模式
简单工厂模式(Simple Factory Pattern)属于类的创新型模式,又叫静态工厂方法模式。是通过专门定义一个类来负责创建其他类的实例,被创建的实例通常都具有共同的父类。简单工厂模式是由一个工厂对象决定创建出哪一种产品类的实例。简单工厂模式是工厂模式家族中最简单实用的模式,可以理解为是不同工厂模式的一个特殊实现。
- maven笔记
zhb8015
maven
跳过测试阶段:
mvn package -DskipTests
临时性跳过测试代码的编译:
mvn package -Dmaven.test.skip=true
maven.test.skip同时控制maven-compiler-plugin和maven-surefire-plugin两个插件的行为,即跳过编译,又跳过测试。
指定测试类
mvn test
- 非mapreduce生成Hfile,然后导入hbase当中
Stark_Summer
maphbasereduceHfilepath实例
最近一个群友的boss让研究hbase,让hbase的入库速度达到5w+/s,这可愁死了,4台个人电脑组成的集群,多线程入库调了好久,速度也才1w左右,都没有达到理想的那种速度,然后就想到了这种方式,但是网上多是用mapreduce来实现入库,而现在的需求是实时入库,不生成文件了,所以就只能自己用代码实现了,但是网上查了很多资料都没有查到,最后在一个网友的指引下,看了源码,最后找到了生成Hfile
- jsp web tomcat 编码问题
王新春
tomcatjsppageEncode
今天配置jsp项目在tomcat上,windows上正常,而linux上显示乱码,最后定位原因为tomcat 的server.xml 文件的配置,添加 URIEncoding 属性:
<Connector port="8080" protocol="HTTP/1.1"
connectionTi
![]()
![]()
![]()
![]() %p,如果你知道b%p的逆元是c,那么就可以转变成
%p,如果你知道b%p的逆元是c,那么就可以转变成 ![]()
![]()
![]()
![]() %p = a*c%p = (a%p)(c%p)%p
%p = a*c%p = (a%p)(c%p)%p![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]() ,所以有
,所以有 ![]()
![]()
![]()
![]()
![]()
![]() %p≡1!对比逆元的定义可得,
%p≡1!对比逆元的定义可得, ![]()
![]()
![]()
![]() 是a的逆元!
是a的逆元!![]()
![]()
![]()
![]() ,即变成求快速幂的问题了(当然这需要满足p为素数)。
,即变成求快速幂的问题了(当然这需要满足p为素数)。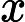
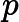

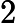 ,因此通过快速幂,求解
,因此通过快速幂,求解 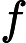





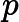

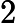 %p,记为M
%p,记为M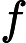







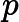

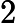 %p,记为NM
%p,记为NM
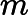
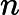

 = ((fac[n]*M)%p*NM)%p
= ((fac[n]*M)%p*NM)%p