深度学习的基础 - 导数是什么 - 微分是什么 - 导数和微分有什么区别 - 微分解决什么问题

导数是什么 - 微分是什么 - 导数和微分有什么区别 - 微分解决什么问题

flyfish

柯西和维尔斯特拉斯时代的极限微积分

无穷数列

我们先从无穷说起。
怎么理解无穷？
我们的分析是在标准分析范围内，如果是非标准分析又是另一套方法
从$\sqrt{2}$说起
相同的两个数相乘，结果是2

一个数和自己相乘结果是2,那么这个数是多少呢？根据这个问题了解无穷小数是怎样产生的，从而了解无穷的样子。

因为
$1^2=1$，$1小于2$，
$2^2=4$，$4大于2$,
所以
这个小数肯定在$1和2$之间。

如果一一计算是$1.1^2$ ,$1.2^2$,$1.3^2$，一直到$1.9^2$，
因为
$1.4^2=1.96$,$1.96小于2$，
而$1.52=2.25$,$2.25大于2$。
所以肯定在$1.4和1.5$之间。
所以小数展开一定是以$1.4$开头

现在假设已经以此方法算出的数字是1.4142135。那么可以继续往下计算

$$\begin{array}{l}1.41421350^2=1.9999998236822500\\ 1.41421351^2=1.9999998519665201\\ 1.41421352^2=1.9999998802507904\\ 1.41421353^2=1.9999999085350609\\ 1.41421354^2=1.9999999368193316\\ 1.41421355^2=1.9999999651036025\\ 1.41421356^2=1.9999999933878736\\ 1.41421357^2=2.000000022\end{array}$$

这样我们得到下一位数字是6。

这样的计算永远无法结束

是什么让我们能够相信存在这样的一个无穷小数 $X^2=2$呢？
我们下面的规律

$$\begin{array}{c}{1}^2=1\\ 1.4^2=1.96\\ 1.41^2=1.9881\\ 1.414^2=1.999396\\ 1.4142^2=1.99996164\\ 1.41421^2=1.9999899241\\ 1.414213^2=1.999998409469\\ 1.4142135^2=1.99999982368225\\ 1.41421356^2=1.9999999933878736\end{array}$$

先确定个概念，因数和积，用于我们后面的表达。
10（因数） ×20（因数） = 200（积）
我们根据上面的列表看到因数的小数位数越多，结果积的小数点后面的数字9就越多。因此，如果把该列表永远的写下去，那么后面的9有无穷多位。这样我们感知到了无穷。
那么问题又来了。
1.99999999…（9无限循环）等于2吗？

极限

$\sqrt{2}$表示为有理数组成的无穷数列，不只一种方法表示。
不足近似值构成的无穷数列
$$\{1.4,1.41,1.414,\dots \}$$
过剩近似值构成的无穷数列
$$\{1.5,1.42,1.415,\dots \}$$

我们再来看$1.99999999\dots 和2$的问题
我们可以看成数列
$$\{1.9,1.99,1.999,\dots \}$$

$$\{2,2,2,2,\dots \}$$
这两个数列都收敛于2

于是我们可以这样写$$\{1.9,1.99,1.999,\dots \}=\{2,2,2,2,\dots \}$$
简写
$$1.99999999\dots =2$$
$1.99999999\dots$看作有理数列$1.9,1.99,1.999,\dots$，其极限是2
$2,2,2,2,\dots$的极限也是2,他们两个叫等价类。

思考过程是 数列-》极限

导数和微分 在不同时期有不同的定义
三种微积分
牛顿和莱布尼茨时代的微积分称之为古典微积分
柯西和维尔斯特拉斯时代的微分称为极限微积分
20世纪60年代鲁滨逊时期的微积分在非标准分析中。
教科书高等数学用的是极限微积分。

古典微积分是上存在bug的，而且是引发第二次数学危机的问题。我们先从严谨的极限微积分说起，在反过来说古典微积分的问题出在什么地方。关于导数和微分这两种微积分中是谁是基础的问题
在极限微积分中先有极限再有导数后有微分。先有导数再有切线。
数列-》极限-》导数-》微分
导数-》切线

导数，切线，微分都体现在下图中

导数

先看导数的定义，再解释
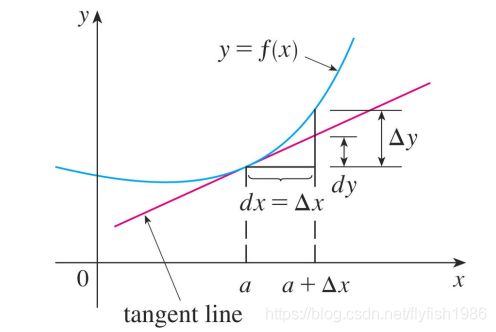
按照《同济大学数学系列教材高等数学上册》导数的定义如下,为了符合图上的字母，我只是把$x_0$换成了 $a$

设函数$y=f(x)$在点$a$的某个邻域内有定义，当$x$在$a$
处增量为$△x(a+△x$仍在该邻域内)时，相应的函数取得增量$△y=f\left(a+\Delta x\right)-f\left(a\right)$.如果$$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(a+\Delta x\right)-f\left(a\right)}{\Delta x}$$
存在，则称该极限为$y=f(x)$在点$a$
处的导数，记为
$$f^{\prime }\left(a\right),{y^{\prime }|}_{x=a},{{\frac{dy}{dx}|}_{x=a}，\frac{df(x)}{dx}|}_{x=a}$$
也称函数$y=f(x)$在点$a$处可导。
可以下列形式表达
（1）
$$f^{\prime }\left(a\right)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(a+\Delta x\right)-f\left(a\right)}{\Delta x}$$
（2）
$$f^{\prime }\left(a\right)=\underset{h\to 0}{\lim }\frac{f\left(a+h\right)-f\left(a\right)}{h}$$
（3）
$$f^{\prime }\left(a\right)=\underset{x\to a}{\lim }\frac{f(x)-f\left(a\right)}{x-a}$$

这里用的$a$，而图上用的字母 $a$

微分

$$\Delta y=f\left(a+\Delta x\right)-f\left(a\right)=A\cdot \Delta x+o(\Delta x)$$
$$dy=A\cdot \Delta x$$

将 $\Delta y$ 表示成 $\Delta x$ 的线性函数, 即线性化, 从而把复杂问题化为简单问题. 即线性化, 从而把复杂问题化为简单问题. 微分就是实现这种线性化的一种数学模型.

按照上图的表示可以这样写
$$f(a+dx)\approx f(a)+dy$$
我们看看实现线性化的数学模型是怎么解决问题的

我们使用函数$f(x)=\sqrt{x+4}$来求$\sqrt{16.05}$的近似值
可以根据图上的字母来
$$\Delta y\approx dy$$
$$\Delta y=f(a+\Delta x)-f(a)$$
$$f(a+dx)-f(a)\approx dy$$
$$f(a+dx)\approx f(a)+dy$$
根据上面的式子就可以这样写

$$\begin{array}{rl}& dy=f^{\prime }(x)dx=\frac{1}{2\sqrt{x+4}}dx\\ & \text{ If }a=12\text{ and }dx=\Delta x=0.05\text{ then }\\ & dy=\frac{1}{2\sqrt{12+4}}0.05=0.00625\\ & \text{ 现在, }\\ & \sqrt{16.05}\\ & =f(12.05)\\ & =f(12+0.05)\\ & \approx f(12)+dy\\ & =4+0.00625=4.00625\end{array}$$

微分定义
设函数$y=f(x)$定义在点$U(x_0)$上,当给$x_0$一个增量$\Delta x,x_0+\Delta x\in U(x_0)$时,相应地得到函数增量为$\Delta y=f(x_0+\Delta x)-f(x_0)$

若$\exists A$,使得$\Delta y=A\Delta x+o(\Delta x)$,则称函数$f$在点$x_0$可微,并称$A\Delta x$为$f$在点$x_0$的微分,记作$dy{|}_{x=x_0}=A\Delta x$或$df(x){|}_{x=x_0}=A\Delta x$

$dy$是$\Delta x$的线性函数,$A\ne 0$时,称微分$dy$为增量$\Delta y$的线性主部

牛顿和莱布尼茨时代的古典微积分

该微积分是以无穷小量为基础搭建的，看上面的极限微积分，基础的定义没有无穷小量的影子。
关于无穷小量这可是引发第二次数学危机的问题
1734年，英国著名的唯心主义哲学家贝克莱主教（Bishop George Berkeley，1685～1753）发现了一个问题
贝克莱说你看这个式子，你要计算$y=f(x)=x^2$的导数
$$\begin{array}{rl}\frac{\Delta y}{\Delta x}& =\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{(x+\Delta x{)}^2-x^2}{\Delta x}\\ & =\frac{x^2+2x\bullet \Delta x+(\Delta x{)}^2-x^2}{\Delta x}\\ & =2x+\Delta x\end{array}$$
牛顿你的无穷小量$\Delta x$先不是0，最后那一步$\Delta x=0$，求得导数为$2x$。
大主教贝克莱说你这个无穷小一会儿是0一会儿不是0，我已经被你们数学家绕晕了，你们没说法，那我就叫它幽灵。你牛顿和莱布尼茨解释解释这个bug你怎么修复。
贝克莱以渺小的哲学家之名出版了一本书，标题很长，不一般的长，题目是《分析学家；或一篇致一位不信神数学家的论文，其中审查一下近代分析学的对象、原则及论断是不是比宗教的神秘、信仰的要点有更清晰的表达，或更明显的推理》。
题目是不是太长了，为什么不起的短一点。
主要还是我们翻译的问题，没有处理，直译的。
我们看其他外文书籍的直译，《国富论》全名是《国民财富的性质和原因的研究》，
《物种起源》全名《论依据自然选择即在生存斗争中保存优良族的物种起源》题目长这是有传统的。
那牛顿是如何回答大主教贝克莱的？牛顿说：你说啥，我听不见。
因为牛顿虽然曾试图通过完善自己的理论来解决，但都没有获得完全成功。这使数学家们陷入了尴尬境地：一方面微积分确实可以解决很多问题，另一方面其自身却存在着逻辑矛盾，即“贝克莱悖论”。这一问题的提出在当时的数学界引起了一定的混乱。
贝克莱主教的问题在思想上和方法上深刻影响了近代数学的发展，由此导致了第二次数学危机的产生。
牛顿和莱布尼茨时代的大师们都有只可意会，不可言传的功夫。大家都能微积分的bug之上正常的工作。但是这个bug又修复不了。到了极限微积分，整个地基都变了，无穷小量被抛弃了。
现在教科书对无穷小量是这么说的，
定义：设f在$U^{\circ }(x_0)$上有定义,若$\underset{x\to x_0}{\lim }f(x)=0$,则称函数$f(x)$为当$x\to x_0$时的无穷小.
也可以用$\epsilon -\delta (epsilon，delta)$语言描述。
在鲁滨逊的非标准分析中，无穷小量又回到了微积分中。