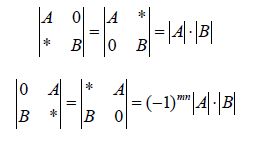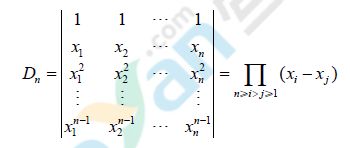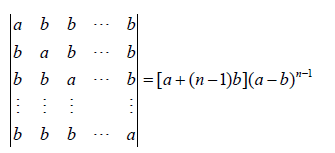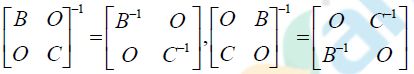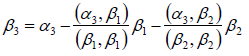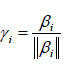线性代数知识点总结_【化重点】线性代数知识点总结
行列式
一、行列式概念和性质
1、逆序数：所有的逆序的总数
2、行列式定义：不同行不同列元素乘积代数和
3、行列式性质：(用于化简行列式)
(1)行列互换(转置)，行列式的值不变
(2)两行(列)互换，行列式变号
(3)提公因式：行列式的某一行(列)的所有元素都乘以同一数k，等于用数k乘此行列式
(4)拆列分配：行列式中如果某一行(列)的元素都是两组数之和，那么这个行列式就等于两个行列式之和。
(5)一行(列)乘k加到另一行(列)，行列式的值不变。
(6)两行成比例，行列式的值为0。
二、重要行列式
1、上(下)三角(主对角线)行列式的值等于主对角线元素的乘积
2、副对角线行列式的值等于副对角线元素的乘积乘
3、Laplace展开式：(A是m阶矩阵，B是n阶矩阵)，则
4、n阶(n≥2)范德蒙德行列式
★5、对角线的元素为a，其余元素为b的行列式的值：
三、按行(列)展开
1、按行展开定理：
(1)任一行(列)的各元素与其对应的代数余子式乘积之和等于行列式的值
(2)行列式中某一行(列)各个元素与另一行(列)对应元素的代数余子式乘积之和等于0
四、克莱姆法则
1、克莱姆法则：
(1)非齐次线性方程组的系数行列式不为0，那么方程为唯一解
(2)如果非齐次线性方程组无解或有两个不同解，则它的系数行列式必为0
(3)若齐次线性方程组的系数行列式不为0，则齐次线性方程组只有0解；如果方程组有非零解，那么必有D=0。
矩阵
一、矩阵的运算
1、矩阵乘法注意事项：
(1)矩阵乘法要求前列后行一致；
(2)矩阵乘法不满足交换律；(因式分解的公式对矩阵不适用，但若B=E,O,A-1，A*,f(A)时，可以用交换律)
(3)AB=O不能推出A=O或B=O。
二、矩阵的逆运算
1、逆的求法：
(1)A为抽象矩阵：由定义或性质求解
(2)A为数字矩阵：(A|E)→初等行变换→(E|A-1)
三、矩阵的初等变换
1、初等行(列)变换定义：
(1)两行(列)互换；
(2)一行(列)乘非零常数c
(3)一行(列)乘k加到另一行(列)
★四、矩阵的秩
1、秩的定义：非零子式的最高阶数
注：
(1)r(A)=0意味着所有元素为0，即A=O
(2)r(An×n)=n(满秩)←→|A|≠0←→A可逆；r(A)＜n←→|A|=0←→A不可逆；
(3)r(A)=r(r=1、2、…、n-1)←→r阶子式非零且所有r+1子式均为0。
2、秩的求法：
(1)A为抽象矩阵：由定义或性质求解；
(2)A为数字矩阵：A→初等行变换→阶梯型(每行第一个非零元素下面的元素均为0)，则r(A)=非零行的行数
五、伴随矩阵
六、分块矩阵
1、分块矩阵的乘法：要求前列后行分法相同。
2、分块矩阵求逆：
向量
一、向量的概念及运算
1、长度定义：||α||= 
二、线性组合和线性表示
1、线性表示的充要条件：
非零列向量β可由α1，α2，…，αs线性表示
(1)←→非齐次线性方程组(α1，α2，…，αs)(x1，x2，…，xs)T=β有解。
★(2)←→r(α1，α2，…，αs)=r(α1，α2，…，αs，β)(系数矩阵的秩等于增广矩阵的秩，用于大题第一步的检验)
2、线性表示的充分条件：
若α1，α2，…，αs线性无关，α1，α2，…，αs，β线性相关，则β可由α1，α2，…，αs线性表示。
3、线性表示的求法：(大题第二步)
设α1，α2，…，αs线性无关，β可由其线性表示。
(α1，α2，…，αs|β)→初等行变换→(行最简形|系数)
行最简形：每行第一个非0的数为1，其余元素均为0
三、线性相关和线性无关
1、线性相关注意事项：
(1)α线性相关←→α=0
(2)α1，α2线性相关←→α1，α2成比例
2、线性相关的充要条件：
向量组α1，α2，…，αs线性相关
(1)←→有个向量可由其余向量线性表示；
(2)←→齐次方程(α1，α2，…，αs)(x1，x2，…，xs)T=0有非零解；
★(3)←→r(α1，α2，…，αs)＜s 即秩小于个数
3、线性相关的充分条件：
(1)向量组含有零向量或成比例的向量必相关
(2)部分相关，则整体相关
(3)高维相关，则低维相关
(4)以少表多，多必相关
★推论：n+1个n维向量一定线性相关
4、线性无关的充要条件：
向量组α1，α2，…，αs线性无关
(1)←→任意向量均不能由其余向量线性表示；
(2)←→齐次方程(α1，α2，…，αs)(x1，x2，…，xs)T=0只有零解
(3)←→r(α1，α2，…，αs)=s
特别地，n个n维向量α1，α2，…，αn线性无关
←→r(α1，α2，…，αn)=n ←→|α1，α2，…，αn |≠0 ←→矩阵可逆
5、线性无关的充分条件：
(1)整体无关，部分无关
(2)低维无关，高维无关
(3)正交的非零向量组线性无关
(4)不同特征值的特征向量无关
6、线性相关、线性无关判定
(1)定义法
★(2)秩：若小于阶数，线性相关；若等于阶数，线性无关
四、极大线性无关组与向量组的秩
1、极大线性无关组不唯一
2、向量组的秩:极大无关组中向量的个数成为向量组的秩
对比：矩阵的秩:非零子式的最高阶数
★注:
向量组α1，α2，…，αs的秩与矩阵A=(α1，α2，…，αs)的秩相等
★3、极大线性无关组的求法
(1)α1，α2，…，αs为抽象的：定义法
(2)α1，α2，…，αs为数字的：(α1，α2，…，αs)→初等行变换→阶梯型矩阵
则每行第一个非零的数对应的列向量构成极大无关组
五、Schmidt正交化
1、Schmidt正交化
设α1，α2，α3线性无关
(1)正交化
令β1=α1
(2)单位化
线性方程组
一、解的判定与性质
1、齐次方程组：
(1)只有零解←→r(A)=n(n为A的列数或是未知数x的个数)
(2)有非零解←→r(A)＜n
2、非齐次方程组：
(1)无解←→r(A)＜r(A|b)←→r(A)=r(A)-1
(2)唯一解←→r(A)=r(A|b)=n
(3)无穷多解←→r(A)=r(A|b)＜n
3、解的性质：
(1)若ξ1，ξ2是Ax=0的解，则k1ξ1+k2ξ2是Ax=0的解
(2)若ξ是Ax=0的解，η是Ax=b的解，则ξ+η是Ax=b的解
(3)若η1，η2是Ax=b的解，则η1-η2是Ax=0的解
二、基础解系
★1、重要结论：(证明也很重要)
设A是m×n阶矩阵，B是n×s阶矩阵，AB=O
(1)B的列向量均为方程Ax=0的解
(2)r(A)+r(B)≤n
2、总结：基础解系的求法
(1)A为抽象的：由定义或性质凑n-r(A)个线性无关的解
(2)A为数字的：A→初等行变换→阶梯型
自由未知量分别取1,0,0；0,1,0；0,0,1；代入解得非自由未知量得到基础解系
三、解的结构(通解)
1、齐次线性方程组的通解(所有解)
设r(A)=r，ξ1，ξ2，…，ξn-r为Ax=0的基础解系，
则Ax=0的通解为k1η1+k2η2+…+kn-rηn-r (其中k1，k2，…，kn-r为任意常数)
2、非齐次线性方程组的通解
设r(A)=r，ξ1，ξ2，…，ξn-r为Ax=0的基础解系，η为Ax=b的特解，
则Ax=b的通解为η+ k1η1+k2η2+…+kn-rηn-r (其中k1，k2，…，kn-r为任意常数)
特征值与特征向量
一、矩阵的特征值与特征向量
1、特征值、特征向量的定义：
设A为n阶矩阵，如果存在数λ及非零列向量α，使得Aα=λα，称α是矩阵A属于特征值λ的特征向量。
2、特征多项式、特征方程的定义：
|λE-A|称为矩阵A的特征多项式(λ的n次多项式)。
|λE-A |=0称为矩阵A的特征方程(λ的n次方程)。
注:特征方程可以写为|A-λE|=0
3、重要结论：
(1)若α为齐次方程Ax=0的非零解，则Aα=0·α，即α为矩阵A特征值λ=0的特征向量
(2)A的各行元素和为k，则(1，1，…，1)T为特征值为k的特征向量。
(3)上(下)三角或主对角的矩阵的特征值为主对角线各元素。
△4、总结：特征值与特征向量的求法
(1)A为抽象的：由定义或性质凑
(2)A为数字的：由特征方程法求解
5、特征方程法：
(1)解特征方程|λE-A|=0，得矩阵A的n个特征值λ1，λ2，…，λn
注：n次方程必须有n个根(可有多重根，写作λ1=λ2=…=λs=实数，不能省略)
(2)解齐次方程(λiE-A)=0，得属于特征值λi的线性无关的特征向量，即其基础解系(共n-r(λiE-A)个解)
二、相似矩阵
1、相似矩阵的定义：
设A、B均为n阶矩阵，如果存在可逆矩阵P使得B=P-1AP，称A与B相似，记作A~B
2、相似矩阵的性质
(1)若A与B相似，则f(A)与f(B)相似
(2)若A与B相似，B与C相似，则A与C相似
(3)相似矩阵有相同的行列式、秩、特征多项式、特征方程、特征值、迹(即主对角线元素之和)
三、矩阵的相似对角化
1、相似对角化定义：如果A与对角矩阵相似，即存在可逆矩阵P，使得P-1AP=Λ=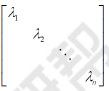
称A可相似对角化。
2、相似对角化的充要条件
(1)A有n个线性无关的特征向量
(2)A的k重特征值有k个线性无关的特征向量
3、相似对角化的充分条件：
(1)A有n个不同的特征值(不同特征值的特征向量线性无关)
(2)A为实对称矩阵
4、重要结论：
(1)若A可相似对角化，则r(A)为非零特征值的个数，n-r(A)为零特征值的个数
(2)若A不可相似对角化，r(A)不一定为非零特征值的个数
四、实对称矩阵
1、性质
(1)特征值全为实数
(2)不同特征值的特征向量正交
(3)A可相似对角化，即存在可逆矩阵P使得P-1AP=Λ
(4)A可正交相似对角化，即存在正交矩阵Q，使得Q-1AQ=QTAQ=Λ
二次型
一、二次型及其标准形
1、二次型：
(1)一般形式
(2)矩阵形式(常用)
2、标准形：
如果二次型只含平方项，这样的二次型称为标准形(对角线)
3、二次型化为标准形的方法：
(1)配方法：
★(2)正交变换法：
二、惯性定理及规范形
1、定义：
正惯性指数：标准形中正平方项的个数称为正惯性指数，记为p；
负惯性指数：标准形中负平方项的个数称为负惯性指数，记为q；
2、惯性定理：
二次型无论选取怎样的可逆线性变换为标准形，其正负惯性指数不变。
注：
(1)由于正负惯性指数不变，所以规范形唯一。
(2)p=正特征值的个数，q=负特征值的个数，p+q=非零特征值的个数=r(A)
三、合同矩阵
1、定义：
A、B均为n阶实对称矩阵，若存在可逆矩阵C，使得B=CTAC，称A与B合同
△2、总结：n阶实对称矩阵A、B的关系
(1)A、B相似(B=P-1AP)←→相同的特征值
(2)A、B合同(B=CTAC)←→相同的正负惯性指数←→相同的正负特征值的个数
(3)A、B等价(B=PAQ)←→r(A)=r(B)
注：实对称矩阵相似必合同，合同必等价
四、正定二次型与正定矩阵
1、正定的定义
二次型xTAx，如果任意x≠0，恒有xTAx＞0，则称二次型正定，并称实对称矩阵A是正定矩阵。
2、n元二次型xTAx正定充要条件：
(1)A的正惯性指数为n
(2)A与E合同，即存在可逆矩阵C，使得A=CTC或CTAC=E
(3)A的特征值均大于0
(4)A的顺序主子式均大于0(k阶顺序主子式为前k行前k列的行列式)
3、总结：二次型正定判定(大题)
(1)A为数字：顺序主子式均大于0
(2)A为抽象：①证A为实对称矩阵：AT=A；②再由定义或特征值判定
4、重要结论：
(1)若A是正定矩阵，则kA(k＞0)，Ak，AT，A-1，A*正定
(2)若A、B均为正定矩阵，则A+B正定
收集整理：安婷
编辑：张润宇
主审：齐蓉 王安东
