SVM多分类应用——基于支持向量机的两组分混合气体四分类定性识别

基于支持向量机的两组分混合气体四分类定性识别

支持向量机

支持向量机（SVM）是一种二分类模型，它的特征是找出一种分割超平面做到分类的间隔最大化，其中超平面即为将数据分成两类的边界，支持向量则是距离这个超明面距离最近的点的坐标，间距为支持向量到超平面距离的二倍。这种分类方式使它在线性分类中有别于感知机模型。支持向量机学习算法是求解凸二次规划的最优化算法。

支持向量机学习模型的核心是核函数，选择一个适合模型的核函数，并有效地调整函数的参数，才能训练出适合模型的支持向量机分类超平面。核函数的选择上大致可以分为线性核函数和非线性核函数。

线性核函数任务是找出合适的参数，使得分割超平面间距最大，且能正确对数据进行分类。间距最大是优化目标要正确地对数据分类是约束条件。

对于线性不可分的模型，高斯核函数就是一个很好的选择了。它的主要作用就是把输入特征映射到另外一组特征上。它的优点是可以把特征映射到无限多维，参数也比较好选择。而缺点则是不容易解释，计算速度比较慢，容易过拟合。高斯核函数的表现形式为：

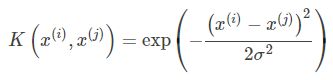
如果输入的特征是一维的标量，那么高斯核函数对应的形状就是一个类似正态分布的反钟形的曲线，其参数σ控制反钟形的宽度。

MATLAB仿真

该仿真模型是在matlab的环境下，运用支持向量机的原理，采用了高斯核函数对数据集进行训练，最终对训练集进行进行四分类。训练完成后，用测试集进行回归检验，并进行评价。

首先要对数据集进行预处理，该模型作为示例没有用很多训练集去严格的优化支持向量机的性能，在搭建模型完成后，仅通过调整不同的参数去观察参数对于分类结果的影响。

下图为数据集EXCEL表’train.xls’从A1到H64，数据集64组，测试集11组。

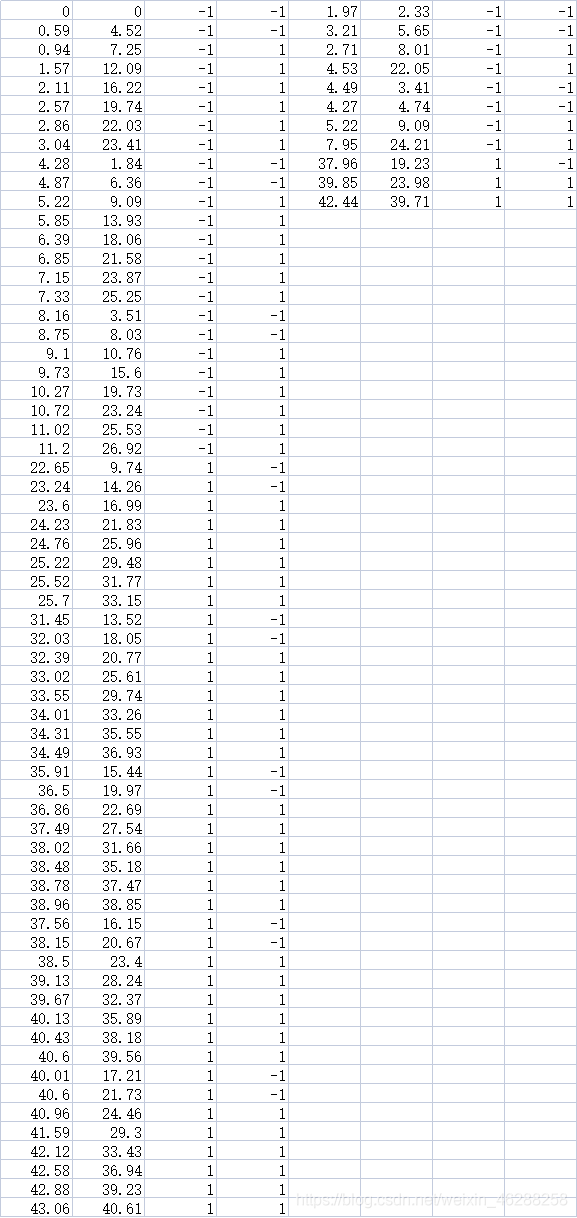
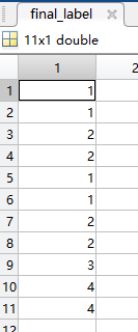
该数据集每组数据两个标签，根据两个标签不同状态，将数据集分成四类，分别是（-1，-1），（-1，1），（1，-1），（1，1）之后在整合成一个新的标签分成1，2，3，4贴在数据集上。

接下来就是设置支持向量机的参数，模型最终选用了高斯核函数对数据集进行处理，数据集对于线性分类的表现并不优秀，高斯核函数的表现更好并且优点是参数更容易选择。

设置好支持向量机的参数后，用matlab自带的fitcsvm函数对训练集进行训练。在fitcsvm是matlab中替代了svmtrain函数的官方的函数，在使用这个函数时需要根据支持向量机的目的对多个参数进行设置：

SVMMODEL = fitcsvm(train_data,train_class,'KernelFunction','gaussian','KernelScale', 10,'BoxConstraint',1000);

train_data是训练样本，可以支持的nxm的训练集矩阵，train_class是样本标签，支持nx1的标签矩阵；‘KernelFunction’,‘gaussian’ 为一对一起使用的参数，有3种 ‘linear’， ‘gaussian’/‘rbf’，‘polynomial’；其他的参数如‘BoxConstraint’,1000 为一对一起使用的参数，是svm的惩罚因子。matlab默认的BoxConstraint为1。参数’KernelScale’,10为键值对参数，表示了高斯核函数的参数取值。

支持向量机是只支持二分类的，对于多分类问题，模型采取了对每一个类都进行一次SVM分类的方法，也就是说对于m个分类需要训练m个二类分类器。对每个类进行一次二分类，当分类到第i个分类器时，把第i类标签置为1，其他类都置为2，这样针对每一个类都需要训练一个二类分类器。测试时对于一个需要分类的测试样本，通常选择最终这个样本在每个SVM二分类器中表现最好的那个类别标记为分类结果。

为了方便观察分类结果，模型对于fitcsvm的分类使用了梯度图进行展示，原理就是，把模型范围规范到训练集二维坐标的最大值最小值之内，在范围内以一定的间隔均匀取点，进行支持向量机的测试，取测试结果最接近0的点连接起来画出分界线，红圈以内的点为支持向量。

第三步，在支持向量机训练好数据之后，对测试集进行回归测试。对四个支持向量机分类模型，均进行测试并把每次分类的结果返回到一个矩阵当中。取出该矩阵每一行的最大值，并返回该值的列数即为最终的测试集标签。

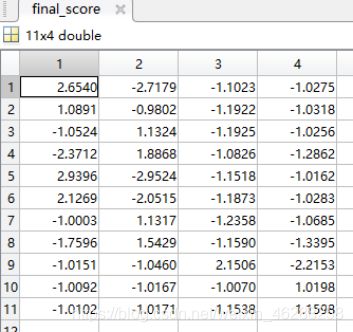
以下为11个测试数据最终权重和分类结果。

最后，测试集预测标签生成之后，将其与测试集真实标签进行对比，对支持向量机的表现进行评价，评价指标采用了confusionmat函数。这是混淆矩阵函数，多用于有监督学习，用于比较分类结果和实际测得值，可以把分类结果的精度显示在一个混淆矩阵里面。

混淆矩阵的主对角线值为预测正确，非主对角线的非零值为预测误差，横向比较为实际值的比较，用于评价预测模型的精确度，纵向比较为预测值得比较，用于评价预测模型的全面程度，以主对角线为中心同时对横向和纵向比较尽心考量，即为预测的精度。

以下为支持向量机的matlab程序：

%读取表格训练集数据
 file_name = 'train.xls';
 train_data = xlsread(file_name,'A1:B64');
 train_label = xlsread(file_name,'C1:D64');
 
 %读取测试集数据
 test_data = xlsread(file_name,'E1:F11');
 test_label = xlsread(file_name,'G1:H11');
 
 %设置4个二分类器
 train_class1 = zeros(64,1);
 train_class2 = zeros(64,1);
 train_class3 = zeros(64,1);
 train_class4 = zeros(64,1);
 train_class = zeros(64,1);
 %将训练集标签填入分类器
 [m,~] = size(train_data);
 for i = 1:m
     if train_label(i,1) == -1
         if train_label(i,2) == -1
             train_class1(i) = 1;
             train_class(i) = 1;
         end
         if train_label(i,2) == 1
             train_class2(i) = 1;
             train_class(i) = 2;
         end
     end
     if train_label(i,1) == 1
         if train_label(i,2) == -1
             train_class3(i) = 1;
             train_class(i) = 3;
         end
         if train_label(i,2) == 1
             train_class4(i) = 1;
             train_class(i) = 4;
         end
     end
 end
 
 %将训练模型进行显示
 figure;
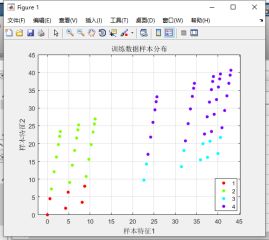
 gscatter(train_data(:,1),train_data(:,2),train_class);
 title('训练数据样本分布');
 xlabel('样本特征1');
 ylabel('样本特征2');
 grid on;
 
 %设置高斯核函数的支持向量机参数
 kernel = 'gaussian';
 sigma = 10;
 C = 1000;
 %对训练集数据分别支持向量机的进行训练
 model1 = fitcsvm(train_data,train_class1,'KernelFunction',kernel,'KernelScale', sigma,'BoxConstraint',C);
 model2 = fitcsvm(train_data,train_class2,'KernelFunction',kernel,'KernelScale', sigma,'BoxConstraint',C);
 model3 = fitcsvm(train_data,train_class3,'KernelFunction',kernel,'KernelScale', sigma,'BoxConstraint',C);
 model4 = fitcsvm(train_data,train_class4,'KernelFunction',kernel,'KernelScale', sigma,'BoxConstraint',C);
 
 %绘制fitcsvm的分界线
 svInd1 = model1.IsSupportVector;
 svInd2 = model2.IsSupportVector;
 svInd3 = model3.IsSupportVector;
 svInd4 = model4.IsSupportVector;
 %设置取点间隔和范围
 h = 0.1;
 max1 = max(train_data(:,1));
 max2 = max(train_data(:,2));
 min1 = min(train_data(:,1));
 min2 = min(train_data(:,2));
 [X1,X2] = meshgrid(min1:h:max1,min2:h:max2);
 %范围内生成模型结果
 [~,score1] = predict(model1,[X1(:),X2(:)]);
 scoreGrid1 = reshape(score1(:,2),size(X1,1),size(X2,2));
 %画图
 figure;
 plot(train_data(:,1),train_data(:,2),'k.');
 hold on;
 plot(train_data(svInd1,1),train_data(svInd1,2),'ro','MarkerSize',10)
 contour(X1,X2,scoreGrid1);
 colorbar;
 title('model1分界线');
 %生成model2图像
 [~,score2] = predict(model2,[X1(:),X2(:)]);
 scoreGrid2 = reshape(score2(:,2),size(X1,1),size(X2,2));
 figure;
 plot(train_data(:,1),train_data(:,2),'k.');
 hold on;
 plot(train_data(svInd2,1),train_data(svInd2,2),'ro','MarkerSize',10)
 contour(X1,X2,scoreGrid2);
 colorbar;
 title('model2分界线');
 %生成model3图像
 [~,score3] = predict(model3,[X1(:),X2(:)]);
 scoreGrid3 = reshape(score3(:,2),size(X1,1),size(X2,2));
 figure;
 plot(train_data(:,1),train_data(:,2),'k.');
 hold on;
 plot(train_data(svInd3,1),train_data(svInd3,2),'ro','MarkerSize',10)
 contour(X1,X2,scoreGrid3);
 colorbar;
 title('model3分界线');
 %生成model4图像
 [~,score4] = predict(model4,[X1(:),X2(:)]);
 scoreGrid4 = reshape(score4(:,2),size(X1,1),size(X2,2));
 figure;
 plot(train_data(:,1),train_data(:,2),'k.');
 hold on;
 plot(train_data(svInd4,1),train_data(svInd4,2),'ro','MarkerSize',10)
 contour(X1,X2,scoreGrid4);
 colorbar;
 title('model4分界线');
 
 %将测试集在4个分类器中分别训练返回其在各个分类器的值
 [label1,fianl_score1] = predict(model1,test_data);
 [label2,final_score2] = predict(model2,test_data);
 [label3,final_score3] = predict(model3,test_data);
 [label4,final_score4] = predict(model4,test_data);
 %将测试后的数据融合
 final_score = [fianl_score1(:,2),final_score2(:,2),final_score3(:,2),final_score4(:,2)];
 final_label = zeros(11,1);
 %返回融合后的标签与位置的最大值和位置，生成最终的标签，完成测试集预测
 [m,~] = size(final_label);
 for i = 1:m
     [~,n] = max(final_score(i,:));
     final_label(i,:) = n;
 end
 %生成测试集实际值
 test_expect = zeros(11,1);
 [m,~] = size(test_expect);
 for i = 1:m
     if test_label(i,1) == -1
         if test_label(i,2) == -1
             test_expect(i) = 1;
         end
         if test_label(i,2) == 1
             test_expect(i) = 2;
         end
     end
     if test_label(i,1) == 1
         if test_label(i,2) == -1
             test_expect(i) = 3;
         end
         if test_label(i,2) == 1
             test_expect(i) = 4;
         end
     end
 end
 
 %测试集显示
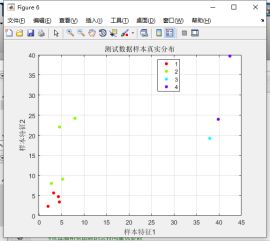
 figure;
 gscatter(test_data(:,1),test_data(:,2),test_expect);
 title('测试数据样本真实分布');
 xlabel('样本特征1');
 ylabel('样本特征2');
 grid on;
 figure;
 gscatter(test_data(:,1),test_data(:,2),final_label);
 title('测试数据样本预测分布');
 xlabel('样本特征1');
 ylabel('样本特征2');
 grid on;
 
 %数据评价
 A = confusionmat(test_expect,final_label,'Order',[1;2;3;4]); 
 [m,~] = size(A);
 for i = 1:m
     c_p = A(i,i) / sum(A(:,i));
     c_r = A(i,i) / sum(A(i,:));
     c_F = 2*c_p*c_r / (c_p + c_r);
     fprintf('第%d类的查准率为%f,查全率为%f,F测度为%f\n\n',i,c_p,c_r,c_F);
 end

仿真结果

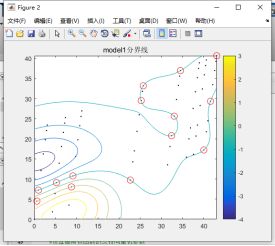
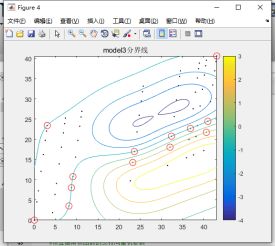
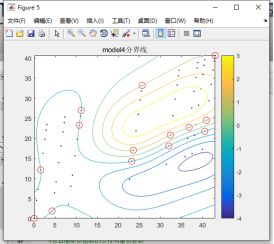
对于核函数的参数调整，高斯核函数自身的参数值越小，分类曲线更加的复杂，分类的边界越陡峭，梯度下降的越快，可能会发生分类超平面过于贴合训练集，进而导致过拟合问题，使分类模型对训练数据过分拟合，而对测试数据预测效果不佳。惩罚因子，值越大分类曲线越复杂，也就是说越容易发生过拟合，过小会因为曲线过于圆滑，对于靠近分界线的测试集点的分类，就可能会有误分类的情况。